Minizinc 代码大全

目录

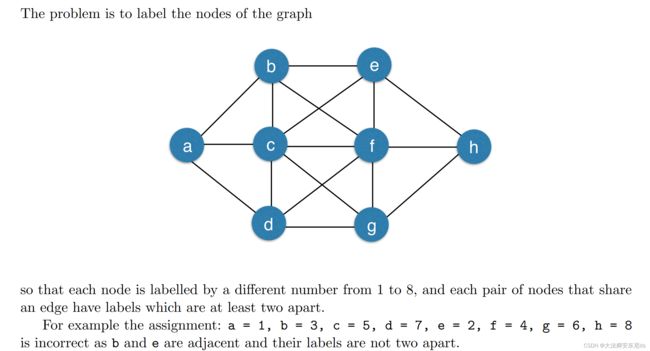
问题1 graphlabel | 逻辑表达式：

如何编写逻辑表达式？

问题2 powergen | array, forall, sum：

问题3 求特定约束下的最大利润 enum, array, assert, max

---

问题1 graphlabel | 逻辑表达式：

如何编写逻辑表达式？

优化建模之MiniZinc(四) 复杂逻辑约束和调度问题实例 - 知乎 (zhihu.com)

var 1..8:a;
var 1..8:b;
var 1..8:c;
var 1..8:d;
var 1..8:e;
var 1..8:f;
var 1..8:g;
var 1..8:h;

constraint (a-b)>=2 \/ (b-a)>=2;
constraint (a-c)>=2 \/ (c-a)>=2;
constraint (a-d)>=2 \/ (d-a)>=2;

constraint (b-c)>=2 \/ (c-b)>=2;
constraint (b-e)>=2 \/ (e-b)>=2;
constraint (b-f)>=2 \/ (f-b)>=2;

constraint (c-d)>=2 \/ (d-c)>=2;
constraint (c-e)>=2 \/ (e-c)>=2;
constraint (c-f)>=2 \/ (f-c)>=2;
constraint (c-g)>=2 \/ (g-c)>=2;

constraint (d-f)>=2 \/ (f-d)>=2;
constraint (d-g)>=2 \/ (g-d)>=2;

constraint (e-f)>=2 \/ (f-e)>=2;
constraint (e-h)>=2 \/ (h-e)>=2;

constraint (f-g)>=2 \/ (g-f)>=2;
constraint (f-h)>=2 \/ (h-f)>=2;

constraint (g-h)>=2 \/ (h-g)>=2;

include "alldifferent.mzn";
constraint alldifferent([a,b,c,d,e,f,g,h]);

问题2 powergen | array, forall, sum：

三种电站，如何投资使得话费最少

约束1：

约束2：

约束3：

 对于约束2，比较好写。

从第一个月到第六个月，只考虑每个月新增的，因为三种核电站的最长寿命是6

从第6个月开始，因为前面至少都有六个数据，所以可以使用便利写法

从第七个月开始，核电站考虑 2...7 日的数据，煤电站考虑第 6 7 日的数据，太阳能电站考虑第 5 6 7日的数据

% power generation
int: T;                 % decades
array[1..T] of int: e;  % expected requirements
array[1..T] of int: a;  % current production

array[1..T] of var 0..infinity: N; % number of nuclear power plants built each decade
array[1..T] of var 0..infinity: C; % number of coal power plants built each decade
array[1..T] of var 0..infinity: S; % number of solar power plants built each decade


% 约束1 前五个月，每个月都有增加
% First month
% the energy available in each decade must meet the expected demand
constraint 4*N[1]+C[1]+S[1]+a[1]>=e[1];
% no more than 40% of all energy can be nuclear in any decade
constraint 4*N[1]<=0.4*(4*N[1]+C[1]+S[1]+a[1]);
% no less than 20% of all energy can be solar in each decade
constraint S[1]>=0.2*(4*N[1]+C[1]+S[1]+a[1]);

% Second month
% the energy available in each decade must meet the expected demand
constraint 4*(N[1]+N[2])+C[2]+C[1]+S[2]+S[1]+a[2]>=e[2];
% no more than 40% of all energy can be nuclear in any decade
constraint 4*(N[1]+N[2])<=0.4*(4*(N[1]+N[2])+C[2]+C[1]+S[2]+S[1]+a[2]);
% no less than 20% of all energy can be solar in each decade
constraint S[1]+S[2]>=0.2*(4*(N[1]+N[2])+C[2]+C[1]+S[2]+S[1]+a[2]);

% 3
% the energy available in each decade must meet the expected demand
constraint 4*(N[1]+N[2]+N[3])+C[3]+C[2]+S[3]+S[2]+S[1]+a[3]>=e[3];
% no more than 40% of all energy can be nuclear in any decade
constraint 4*(N[1]+N[2]+N[3])<=0.4*(4*(N[1]+N[2]+N[3])+C[3]+C[2]+S[3]+S[2]+S[1]+a[3]);
% no less than 20% of all energy can be solar in each decade
constraint S[3]+S[2]+S[1]>=0.2*(4*(N[1]+N[2]+N[3])+C[3]+C[2]+S[3]+S[2]+S[1]+a[3]);

% 4
% the energy available in each decade must meet the expected demand
constraint 4*(N[1]+N[2]+N[3]+N[4])+C[4]+C[3]+S[4]+S[3]+S[2]+a[4]>=e[4];
% no more than 40% of all energy can be nuclear in any decade
constraint 4*(N[1]+N[2]+N[3]+N[4])<=0.4*(4*(N[1]+N[2]+N[3]+N[4])+C[4]+C[3]+S[4]+S[3]+S[2]+a[4]);
% no less than 20% of all energy can be solar in each decade
constraint S[4]+S[3]+S[2]>=0.2*(4*(N[1]+N[2]+N[3]+N[4])+C[4]+C[3]+S[4]+S[3]+S[2]+a[4]);

% 5
% the energy available in each decade must meet the expected demand
constraint 4*(N[1]+N[2]+N[3]+N[4]+N[5])+C[5]+C[4]+S[5]+S[4]+S[3]+a[5]>=e[5];
% no more than 40% of all energy can be nuclear in any decade
constraint 4*(N[1]+N[2]+N[3]+N[4]+N[5])<=0.4*(4*(N[1]+N[2]+N[3]+N[4]+N[5])+C[5]+C[4]+S[5]+S[4]+S[3]+a[5]);
% no less than 20% of all energy can be solar in each decade
constraint S[5]+S[4]+S[3]>=0.2*(4*(N[1]+N[2]+N[3]+N[4]+N[5])+C[5]+C[4]+S[5]+S[4]+S[3]+a[5]);


% 6 第六个月开始滚动
% the energy available in each decade must meet the expected demand
constraint forall(i in 6..T)(4*(N[i-5]+N[i-4]+N[i-3]+N[i-2]+N[i-1]+N[i])+C[i]+C[i-1]+S[i]+S[i-1]+S[i-2]+a[i]>=e[i]);
% no more than 40% of all energy can be nuclear in any decade
constraint forall(i in 6..T)(4*(N[i-5]+N[i-4]+N[i-3]+N[i-2]+N[i-1]+N[i])<=0.4*(4*(N[i-5]+N[i-4]+N[i-3]+N[i-2]+N[i-1]+N[i])+C[i]+C[i-1]+S[i]+S[i-1]+S[i-2]+a[i]));
% no less than 20% of all energy can be solar in each decade
constraint forall(i in 6..T)(S[i]+S[i-1]+S[i-2]>=0.2*(4*(N[i-5]+N[i-4]+N[i-3]+N[i-2]+N[i-1]+N[i])+C[i]+C[i-1]+S[i]+S[i-1]+S[i-2]+a[i]));

%约束3
constraint (sum(i in 1..T)(C[i]*2))-C[T]<=10;
%如果加上太阳能电站不小于10呢？
%constraint (sum(i in 1..T)(S[i]*3))-2*S[T]-S[T-1]>=10;

var 0..infinity: cost = sum(i in 1..T)(N[i]*10+C[i]+S[i]*2);  % costs of building all new power plants

solve minimize cost;
output ["cost:\(cost)\n",        "N:\(N)\n",        "C:\(C)\n",        "S:\(S)\n"];
                           

问题3 求特定约束下的最大利润 enum, array, assert, max

% 简单批量生产计划模型的数据文件
Products = { BananaCake, ChocolateCake };
profit = [400, 450]; % 以分为单位
Resources = { Flour, Banana, Sugar, Butter, Cocoa };
capacity = [4000, 6, 2000, 500, 500];
consumption= [| 250, 2, 75, 100, 0,
| 200, 0, 150, 150, 75 |];

% 要制造的产品
enum Products;
% 每种产品的单位利润，以Products里面的元素按顺序作为数组下标
array[Products] of int: profit;

% 用到的资源
enum Resources;
% 每种资源可获得的数量
array[Resources] of int: capacity;

% 制造一个单位的产品需要的资源单位量
array[Products, Resources] of int: consumption;
% 前者p行数 后者r列数
constraint assert(forall (r in Resources, p in Products)(consumption[p,r] >= 0), "Error: negative consumption");

% 产品数量的界。为什么先取min 再取max？
% 除完了是3 2 1，那么应该以小的为准，只生产1份。
% 两个产品分别可以生产1，3份，那么最多能生产3份
int: mproducts = max (p in Products)(min (r in Resources where consumption[p,r] > 0)(capacity[r] div consumption[p,r]));

% 变量：每种产品我们需要制造多少
array[Products] of var 0..mproducts: produce;
array[Resources] of var 0..max(capacity): used;

% 产量不可以使用超过可获得的资源量：
constraint forall (r in Resources) (used[r] = sum (p in Products)(consumption[p, r] * produce[p]));% 消耗量*数量
constraint forall (r in Resources) (used[r] <= capacity[r]);

% 最大化利润
solve maximize sum (p in Products) (profit[p]*produce[p]);

output [ "\(p) = \(produce[p]);\n" | p in Products ] ++
[ "\(r) = \(used[r]);\n" | r in Resources ];