电动汽车负荷预测——蒙特卡洛法python实现过程

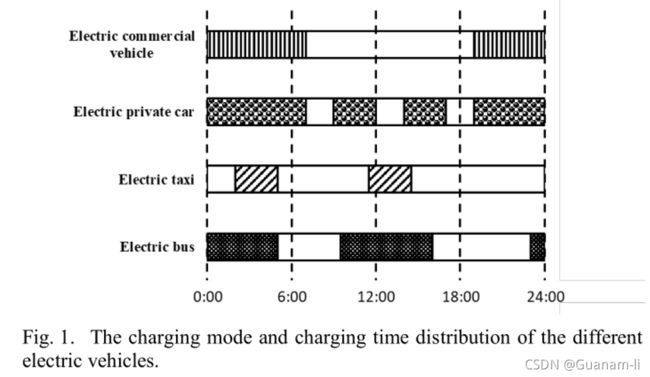
运用蒙特卡洛随机抽样，python代码，模拟一千台电动汽车的一天内的充电负荷。用到的数据大部分来自于论文《Charging Load Forecasting of Electric Vehicle Based on Monte Carlo and Deep Learning》

MonteCarlo电动汽车负荷预测基本思想：

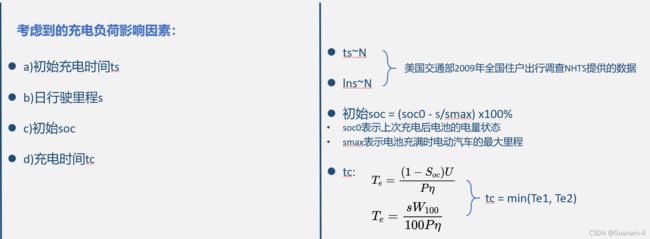
从满足分布的参数中，不停抽取样本。考虑到的因素有：
初始充电时间ts
日行驶里程s
初始soc
充电持续时间tc

1.抽取随机变量：
包括有日行驶里程s（满足对数正态分布），充电开始时间ts（满足正态分布）

2.计算其余变量：
初始soc：不理解论文中所描述，改成soc0 =（1-s/smax）

充电时间tc：$tc=\left(\frac{(1-SO{C}_0)U}{P\eta }\right)$

3.确定目标：

电动汽车（私家车）电池规格：

模拟电动私家车出行规律：

前提假设：

具体条件：

4.考虑细节：
模型简化恒功率充电，方便操作
确定抽取样本没有出现常识性错误，比如soc为负
规定soc线性变化
一天充电一次，确定开始和结束时间，叠加每一辆车的功率
快充改为40kw
抽取三个时间段的样本会互相交错时间
抽取的时间段会延续到24h之后，画图可以将24h之后的图像转为第一天凌晨叠加。

5.python代码实现：

设定种子，python随机数抽取样本

确定充电开始时间和它的标签，用来记录这辆车是在上午下午还是晚上充电，以及确定充电功率，具体形式如下：

选择充电功率，计算持续时间tc，计算结束时间te
给定时间功率二维数组，叠加功率，最后效果如下：

第一辆车：

一天负荷：

过程讲解完毕，代码部分在这：
看懂需要python和numpy基础，b站莫凡python半天过一遍应该够了。
jupyter打开文件
下载地址