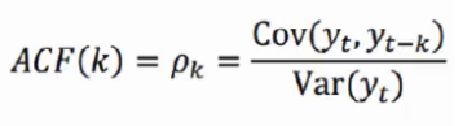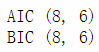Python实现时间序列ARIMA模型
0. ARIMA模型原理
0.1 ARMA和ARIMA
ARMA: 自回归模型与移动平均模型的结合
- AR:自回归模型:顾名思义,就是及时地“回顾”过去,分析数据中先前的值,并对它们做出假设。这些先前的值称为“滞后”。
- MA:移动平均线:该模型的移动平均方面,是将观测值与应用于滞后观测值的移动平均模型的残差之间的相关性合并。
ARIMA(p, d, q)模型: 全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average model, 简称为ARIMA)
- AR和MA与上述ARMA模型等价
- I: 表示综合: 当应用差分步骤时,数据是“综合”的,以消除非平稳性。表示原始观测值的差异,以允许时间序列变得平稳,即数据值被数据值和以前的值之间的差异替换。
原理: 将非平稳时间序列转换为平稳时间序列然后将因变量仅对他的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型
P为自回归项,q为移动平均项数,d为差分次数
0.2 自回归模型(AR)
描述当前值与历史值之间的关系,用变量自身的历史数据对自身进行预测
自回归模型必须满足平稳性的要求(差分法)
P阶自回归过程的公式定义:
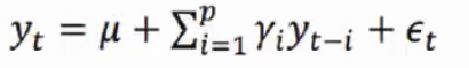

P P P 阶的意思是历史值与前面多少个有关系
- 当 p = 1 p=1 p=1 时,当前值 y t y_t yt 与前1天的 y y y 值有关
- 求和:不仅与前1天有关,和前1天、2天…前 t t t 天都有关
自回归模型(AR)的限制
- 自回归模型是用自身的数据进行预测
- 必须具有平稳性 (平稳性检测)
- 必须具有相关性(数据随时间变化而变化),如果自相关系数( φ i φ_i φi)小于0.5,则不宜采用 (相关性检测)
- 自回归只适用于预测与自身前期相关的现象
平稳性
从统计学的角度来看,平稳性是指数据的分布在时间上平移时不发生变化。要求经由样本时间序列所得到的拟合曲线在未来的一段期间内仍能顺着现有的形态“惯性”地延续下去。因此,非平稳数据显示了由于趋势而产生的波动,必须对其进行转换才能进行分析。
平稳性要求序列的均值和方差不发生明显变化
严平稳与弱平稳:
- 严平稳:严平稳表示的分布不随时间的改变而改变
- 如:白噪音(正态)无论怎么取都是期望为0,方差为一
- 弱平稳:期望与相关系数(依赖性)不变 (大部分情况)
- 未来某时刻的 t t t 的值 X t X_t Xt 就要依赖于它过去的信息,所以需要依赖性
0.3 移动平均模型(MA)
移动平均模型关注的是自回归模型中的误差项的累加
q阶自回归过程的公式定义:

移动平均法能有效地消除预测中的随机波动 (使误差越均衡越好)
0.4 模型参数选择方法
ACF自相关系数
有序的随机变量序列与其自身相比较
自相关函数反映了同一序列在不同时序的取值的相关性
当相关系数为1时为正相关,为-1时为负相关,0为没有关系
公式解释:
变量与自身的变化, y t y_t yt 和 y ( t − 1 ) y_{(t-1)} y(t−1) 到 y t y_t yt 和 y ( t − k ) y_{(t-k)} y(t−k) 的相关系数
k阶滞后点
ρ k \rho_k ρk 的取值范围 [-1,1]
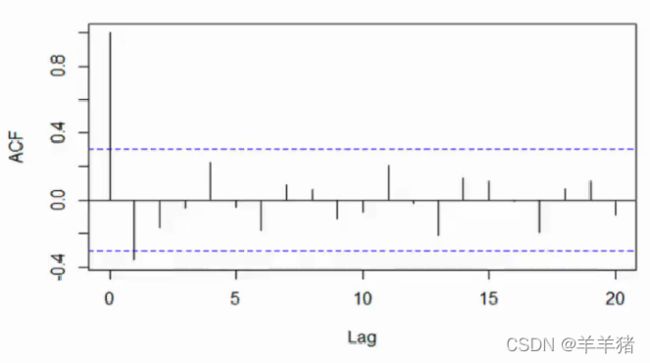
横轴为阶数,纵轴为ACF的值。虚线表示95%置信区间。
这里Lag=20, 则最大为20阶。不同阶代表滞后不同的点。看同一序列在不同阶的时候的相关性如何。
这里2阶的时候约为-0.35,则与自身为负相关,相关系数约为0.35
PACF偏自相关系数
对于一个平稳 A R ( p ) AR(p) AR(p) 模型,求出滞后k自相关系数 p ( k ) p(k) p(k) 时实际上得到的并不是 x ( t ) x(t) x(t) 与 x ( t − k ) x(t-k) x(t−k) 之间单纯的相关关系
x ( t ) x(t) x(t) 同时还会受到中间 k − 1 k-1 k−1 个随机变量 x ( t − 1 ) x(t-1) x(t−1) 、 x ( t − 2 ) x(t-2) x(t−2) ……、 x ( t − k + 1 ) x(t-k+1) x(t−k+1) 的影响,而这 k − 1 k-1 k−1 个随机变量又都和 x ( t − k ) x(t-k) x(t−k) 具有相关关系,所以自相关系数 p ( k ) p(k) p(k) 里实际掺杂了其他变量对 x ( t ) x(t) x(t) 与 x ( t − k ) x(t-k) x(t−k) 的影响
剔除了中间 k − 1 k-1 k−1 个随机变量 x ( t − 1 ) x(t-1) x(t−1) 、 x ( t − 2 ) x(t-2) x(t−2) ……、 x ( t − k + 1 ) x(t-k+1) x(t−k+1) 的干扰之后 x ( t − k ) x(t-k) x(t−k) 对 x ( t ) x(t) x(t) 影响的相关程度
总的来说ACF包含了其他变量的影响而偏自相关系数PACF是严格这两个变量之间的相关性
AIC和BIC
AIC: 赤池信息准则(Akaike Information Criterion)
A I C = 2 k − 2 l n ( L ) AIC = 2k - 2ln(L) AIC=2k−2ln(L)
是参数与最终结果的精度之间的权衡
AIC为模型选择提供了有效的规则,但也有不足之处。当样本容量很大时,在AIC准则中拟合误差提供的信息就要受到样本容量的放大,而参数个数的惩罚因子却和样本容量没关系(一直是2),因此当样本容量很大时,使用AIC准则选择的模型不收敛与真实模型,它通常比真实模型所含的未知参数个数要多。
BIC: 贝叶斯信息准则(Bayesian Information Criterion)
B I C = k l n ( n ) − 2 l n ( L ) BIC = kln(n) - 2ln(L) BIC=kln(n)−2ln(L)
k为模型参数个数,n为样本数量,L为似然函数
AIC和BIC越小越好
参数优化:似然函数最大化,模型中的未知参数个数最小化。
0.5 ARIMA模型建立的一般步骤
- 数据预处理
- 数据检测
2.1 平稳性检测
2.2 白噪声检测(检测是否纯随机数,不是纯随机数才可以做时间序列分析) - 计算ACF、PACF,选取合适的 p p p, q q q 值
- 模型识别
- 模型检测
5.1 残差检验(QQ图)
5.2 正态检验(shapiro)
5.3 Durbin-Watson 检验
5.4 Ljung-Box检验(残差白噪声检验) - 模型预测
- 模型评估
开始建模
1. 数据预处理
1.1 导包
# 这里把所有有可能用到的包都导了
from statsmodels.tsa.stattools import adfuller # 平稳性检测
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf # 画acf, pacf图
from statsmodels.tsa.arima_model import ARIMA # ARIMA模型
from statsmodels.graphics.api import qqplot # 画qq图
from scipy.stats import shapiro # 正态检验
import statsmodels.tsa.stattools as st
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import warnings
import statsmodels
import seaborn as sns
import matplotlib.pylab as plt
from scipy import stats
warnings.filterwarnings('ignore')
matplotlib.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
1.2 数据处理
# 5年里比特币的趋势
df = pd.read_excel('Value_data.xlsx',index_col=0)
ts = df[['Date', 'Value']]
ts = ts.set_index('Date')
#切分为测试数据和训练数据
n_sample = ts.shape[0]
n_train = int(0.95 * n_sample)+1
n_forecast = n_sample - n_train
ts_train = ts.iloc[:n_train]['Value']
ts_test = ts.iloc[n_train:]['Value']
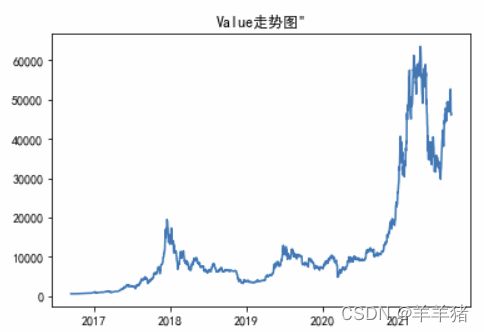
plt.plot(ts)
plt.title('Value走势图"')
plt.show()
# 可以明显看出数据不平稳
1.3 差分法序列平稳化
# 一般做一阶或二阶差分可使序列平稳
diff_df = ts.copy()
diff_df.index=ts.index
# 一阶差分
diff_df['diff_1'] = diff_df.diff(1).dropna()
# 二阶差分
diff_df['diff_2'] = diff_df['diff_1'].diff(1).dropna()
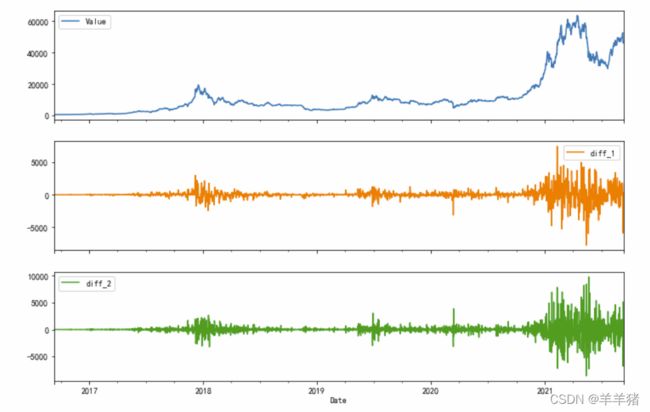
# 作图
diff_df.plot(subplots=True,figsize=(18,20))
plt.show()
# 对比选择几阶差分,肉眼观察数据平稳性
# 这里选择了一阶差分(即 d=1)
ts_diff=ts.copy()
ts_diff.index=ts.index
ts_diff=ts.diff(1).dropna()
2. 数据检测
2.1 平稳性检测
adfuller单位根检验数据平稳性
ADF检验的原假设是存在单位根,只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设,认为数据平稳。注意,ADF值一般是负的,也有正的,但是它只有小于1%水平下的才能认为是及其显著的拒绝原假设。
(原假设为不是平稳时间序列)
# adfuller单位根检验数据平稳性
from statsmodels.tsa.stattools import adfuller
print(adfuller(ts)) # 原始数据
print(adfuller(diff_df['diff_1'].dropna())) # 一阶差分
print(adfuller(diff_df['diff_2'].dropna())) # 二阶差分
输出结果解释:
第一个是adt检验的结果,简称为T值,表示t统计量。
第二个简称为p值,表示t统计量对应的概率值。
第三个表示延迟。
第四个表示测试的次数。
第五个是配合第一个一起看的,是在99%,95%,90%置信区间下的临界的ADF检验的值。
需要看的结果:
第一个,1%、5%、10%不同程度拒绝原假设的统计值和ADF Test result的比较,ADF Test result同时小于1%、5%、10%(第五个结果)即说明非常好地拒绝该假设。
第二个,p值要求小于给定的显著水平,p值要小于0.05,越小越好。P值接近0,则是平稳的,否则,不平稳。
结果分析:
原始数据的P值>0.05所以不满足平稳性要求
一阶差分的P值<0.05,且T值小于1%,5%,10%下的统计值,可以极显著的拒绝原假设,说明数据是平稳的。
一阶差分数据已经平稳就无需继续做二阶差分了。
2.2 白噪声检测
白噪声检验也称为纯随机性检验,当数据是纯随机数据时,再对数据进行分析就没有任何意义了,所以拿到数据后最好对数据进行一个纯随机性检验。
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(ts_diff, lags = 20)
输出结果解释:
lbvalue:测试的统计量
pvalue:基于卡方分布的p统计量
需要看的结果:
pvalue: 越小越好
结果分析:
一阶差分的P值都很小,所以该数据拒绝原假设,即认为该数据不是纯随机数据,即数据可以用于时间序列分析
3. 参数选择
3.1 根据ACF和PACF图肉眼观察
# 画pacf图和acf图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
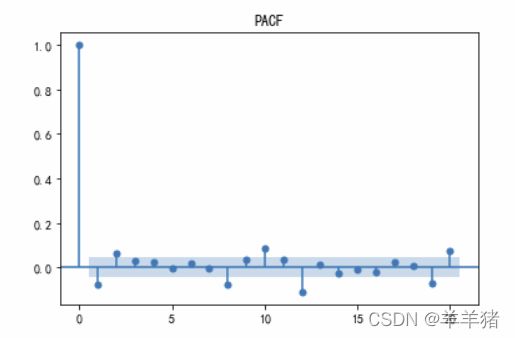
pacf = plot_pacf(ts_diff, lags=40)
plt.title('PACF')
pacf.show()
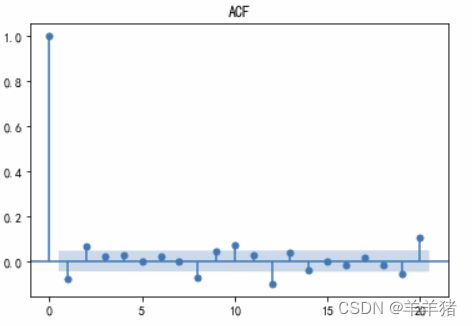
acf = plot_acf(ts_diff, lags=40)
plt.title('ACF')
acf.show()
判断方法
| 模型 | ACF | PACF |
|---|---|---|
| AR(p) | 拖尾,衰减趋于零(几何型或振荡型) | p阶后截尾 |
| MA(q) | q阶后截尾 | 拖尾,衰减趋于零(几何型或振荡型) |
| ARMA(p,q) | 拖尾,q阶后衰减趋于零(几何型或振荡型) | 拖尾,p阶后衰减趋于零(几何型或振荡型) |
| 模型不适合 | 截尾 | 截尾 |
截尾:落在置信区间内( 95%的点都符合该规则)
判断拖尾和结尾:
- 拖尾: 始终有非零取值,不会在大于某阶后就快速趋近于0(而是在0附近波动),可简单理解为无论如何都不会为0,而是在某阶之后在0附近随机变化。
- 截尾: 在大于某阶(k)后快速趋于0为k阶截尾,可简单理解为从某阶之后直接就变为0。
判断解释: (其实这个例子用肉眼看不太好)
先确定p值
- 即看PACF图,在第几阶后落在置信区间内,这里取2或者8都可以,部分突出的可以认为是异常值
- 然后看ACF图,在2或8阶后都可以认为衰减趋于零
然后确定q值
- 即看ACF图,在在第几阶后落在置信区间内,这里取2或者8都可以,部分突出的可以认为是异常值
- 然后看ACF图,在2或8阶后都可以认为衰减趋于零
通常情况下:
- 如果说自相关图拖尾,并且偏自相关图在p阶截尾时,此模型应该为AR§。
- 如果说自相关图在q阶截尾并且偏自相关图拖尾时,此模型应该为MA(q)。
- 如果说自相关图和偏自相关图均显示为拖尾,那么可结合ACF图中最显著的阶数作为q值,选择PACF中最显著的阶数作为p值,最终建立ARMA(p,q)模型。
- 如果说自相关图和偏自相关图均显示为截尾,那么说明不适合建立ARMA模型。
3.2 以BIC最小为标准确定p, q值
循环求BIC值
import itertools
# 这里最大最小的参数可以自己调
p_min = 0
d_min = 0
q_min = 0
p_max = 8
d_max = 1
q_max = 8
# Initialize a DataFrame to store the results,,以BIC准则
results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
for p,d,q in itertools.product(range(p_min,p_max+1),
range(d_min,d_max+1),
range(q_min,q_max+1)):
if p==0 and d==0 and q==0:
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
continue
try:
model = sm.tsa.ARIMA(ts_train, order=(p, d, q),
#enforce_stationarity=False,
#enforce_invertibility=False,
)
results = model.fit()
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.bic
except:
continue
results_bic = results_bic[results_bic.columns].astype(float)
画出热力图
fig, ax = plt.subplots(figsize=(10, 8))
ax = sns.heatmap(results_bic,
mask=results_bic.isnull(),
ax=ax,
annot=True,
fmt='.2f',
)
ax.set_title('BIC')
plt.show()
纵坐标为p, 横坐标为q
选取BIC最小的方格即为选取的参数p, q
这里BIC最小的方格在AR8和MA6的方格里,所以所选参数即为 p=8, q=6
3.3 综合考虑AIC和BIC
# 这里 max_ 数字越大运行时间越长,这里取8运行时间为 13m 13s
train_results = sm.tsa.arma_order_select_ic(ts_train, ic=['aic', 'bic'], trend='nc', max_ar=8, max_ma=8)
print('AIC', train_results.aic_min_order)
print('BIC', train_results.bic_min_order)
这里给出的AIC标准下和BIC标准下的p, q选择一致,所以我们可以直接确定 p=8, q=6为模型最佳参数
如果AIC和BIC标准下的p, q选择不一致,则可以考虑分别把模型fit两组参数,查看AIC和BIC的大小再进行选择,AIC和BIC越小越好。
4. 模型识别
from statsmodels.tsa.arima_model import ARIMA
# ARIMA(data, order=(p, d, q))
model = ARIMA(ts_train, order=(8,1,6))
result = model.fit()
result.summary()
5. 模型检验
5.1 残差检验
# 获取残差
resid = result.resid
# 画qq图
from statsmodels.graphics.api import qqplot
qqplot(resid, line='q', fit=True)
plt.show()
5.2 正态检验(shapiro)
正态性检验可以使用Shapiro Wilk函数来检查,当p-value>0.05时表明满足正态分布,该值越大越好,直到接近于1
from scipy.stats import shapiro
shapiro(resid)
输出:(统计量W的值,P值)
结果:ShapiroResult(statistic=0.7804399490356445, pvalue=0.355424317961812)
因此残差满足正态分布
5.3 自相关性检验(Durbin-Watson)
Durbin-Watson 检验,又称 DW 检验,是用来检验回归分析中残差的一阶自相关性的(尤其针对时间序列数据)。
该统计量值越接近 2 越好,一般在 1~3 之间说明没问题,小于 1 这说明残差存在自相关性
import statsmodels.api as sm
print(sm.stats.durbin_watson(resid.values))
结果: 1.999361458766296
因此残差不存在自相关性
5.4 Ljung-Box检验(残差白噪声检验)
Ljung-Box test是对randomness的检验,或者说是对时间序列是否存在滞后相关的一种统计检验。对于滞后相关的检验,我们常常采用的方法还包括计算ACF和PCAF并观察其图像,但是无论是ACF还是PACF都仅仅考虑是否存在某一特定滞后阶数的相关。LB检验则是基于一系列滞后阶数,判断序列总体的相关性或者说随机性是否存在。
时间序列中一个最基本的模型就是高斯白噪声序列。而对于ARIMA模型,其残差被假定为高斯白噪声序列,所以当我们用ARIMA模型去拟合数据时,拟合后我们要对残差的估计序列进行LB检验,判断其是否是高斯白噪声。如果得到白噪声序列,就说明时间序列中有用的信息已经被提取完毕了,剩下的全是随机扰动,是无法预测和使用的, 残差序列如果通过了白噪声检验,则建模就可以终止了,因为没有信息可以继续提取。如果残差不是白噪声,就说明残差中还有有用的信息,需要修改模型或者进一步提取。
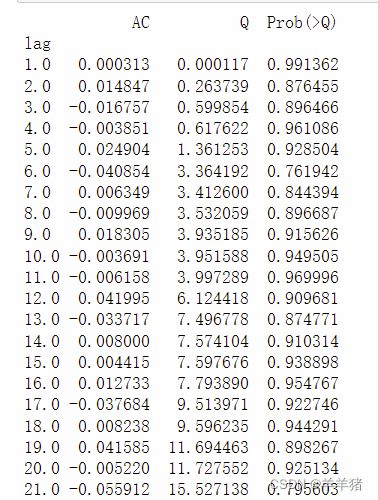
r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
data = np.c_[range(1,21), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))
输出解释:
原假设为白噪声(相关系数为零)检验的结果就是看最后一列前十二行的检验概率(一般观察滞后1~12阶),如果检验概率小于给定的显著性水平,比如0.05、0.10等就拒绝原假设,即为非白噪声。
结果分析:
如果取显著性水平为0.05或者0.1,结果不小于显著性水平,那么相关系数与零没有显著差异,即为白噪声序列。
6. 模型预测
6.1 预测测试集
# 预测出来的数据也为一阶差分
# predict(起始时间,终止时间)
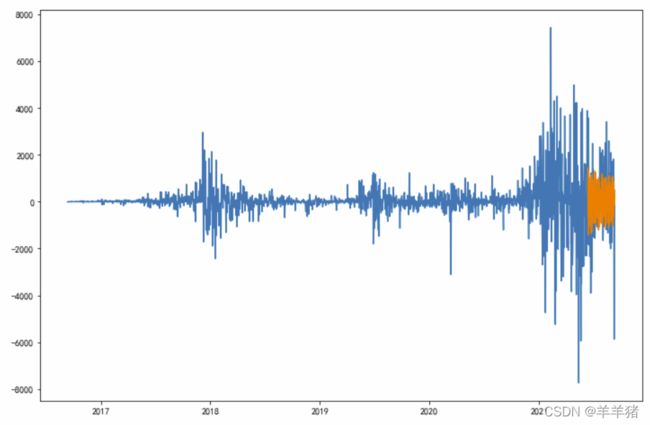
predict = result.predict('2021-06-12','2021-9-10')
plt.figure(figsize=(12, 8))
plt.plot(ts_diff)
plt.plot(predict)
6.2 预测全集数据
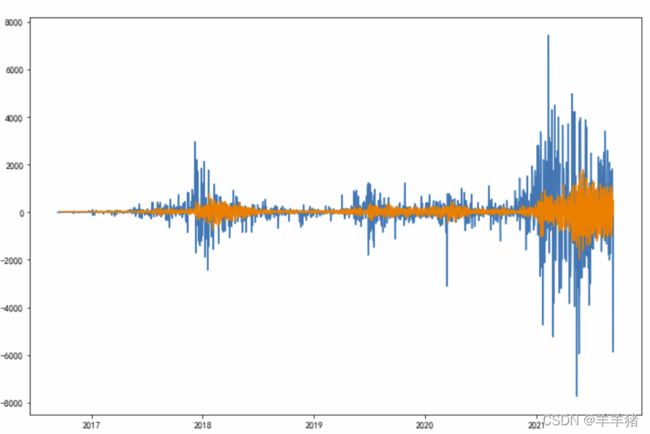
pred_all = result.predict('2016-09-20','2021-9-10')
plt.figure(figsize=(12, 8))
plt.plot(ts_diff)
plt.plot(pred_all)
可以看到总体预测出来的效果还是可以的了
7. 模型评价
因为我们对数据做了一阶差分处理,所以预测出来的数据也是一阶差分,因此在评价模型前应该把测试集也做一阶差分处理
# 测试集做一阶差分
test_diff=ts_test.copy()
test_diff.index=ts_test.index
test_diff=ts_test.diff(1).dropna()
模型预测好坏有很多种评价标准,这里只介绍两种
7.1 MAE:平均绝对误差 – Mean Absolute Error
np.linalg.norm(predict-test_diff, ord=1)/len(predict)
7.2 RMSE:均方根误差 – Root Mean Square Error
np.sqrt(((predict - test_diff) ** 2).mean())
参考来源:
statsmodels.tsa.arima_model.ARIMA.predict
6 ARMA模型
机器学习经典算法:时间序列ARIMA模型
机器学习(五)——时间序列ARIMA模型
理论加实践,终于把时间序列预测ARIMA模型讲明白了
TimeSeries_Predict
python时间序列分析(ARIMA模型)
Statsmodels adfuller平稳性ADF检验
用python实现时间序列白噪声检验
ACF/PACF,残差白噪声的检验问题
时间序列之白噪声检验
【统计与检验-1】Shapiro-Wilk检验
Python机器学习模型-线性回归模型相关检验
回归评价指标MSE、RMSE、MAE、MAPE及python实现
时间序列–ARIMA(寻找最优参数)