简述几种图像增强的算法

1、几种经典的图像增强算法

 

1.1、Retinex

简单来说，直方图均衡化采用的方法是将图像中像素点的直流分量都去掉，只剩下交流分量，然后对交流分量进行归一化、拉伸或者直接输出。

原理：

输入图像由照度分量和反射分量两部分组成，即：
                                                     

其中，L为亮度分量，描述照明，变化缓慢，处于低频部分；R为反射分量，描述景物细节，变化较快，处于高频部分。
Retinex算法对图像的处理目的就是从图像I中获取反射分量R。算法流程如下：

发展：

Retinex算法理论有两个经典算法：基于路径的Retinex以及基于中心环绕Retinex。基于中心环绕Retinex又从单尺度（Single Scale Retinex）到多尺度（Multi Scale Retinex），再发展至带有色彩恢复的多尺度（Multi Scale Retinex with Color Restoration）以及其他更多的改进。在此只学习基于中心环绕的一个典型算法。

单尺度算法（SSR）

 

1.2、直方图均衡化

简单来说，直方图算法来做图像增强是利用了将图像中像素点的直流分量补齐。使得灰度值低的像素点的亮度提高。

直方图的概念
对一幅灰度图像，其直方图反映了该图像中不同灰度级出现的统计情况。图2给出了一个直方图的示例，其中图(a)是一幅图像，其灰度直方图可表示为图(b)，其中横轴表示图像的各灰度级，纵轴表示图像中各灰度级像素的个数。（需要注意，灰度直方图表示了在图像中各个单独灰度级的分布，而图像对比度则取决于相邻近像素之间灰度级的关系。）

直方图均衡化是一种简单有效的图像增强技术，通过改变图像的直方图来改变图像中各像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰。例如，过曝光图像的灰度级集中在高亮度范围内，而曝光不足将使图像灰度级集中在低亮度范围内。采用直方图均衡化，可以把原始图像的直方图变换为均匀分布（均衡）的形式，这样就增加了像素之间灰度值差别的动态范围，从而达到增强图像整体对比度的效果。换言之，直方图均衡化的基本原理是：对在图像中像素个数多的灰度值（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并，从而增大对比度，使图像清晰，达到增强的目的。举个例子，如图1所示，左图为原始图像，右图为直方图均衡化后的图像。

—

 1.3、PDE

2、几种基于经典算法改进的新图像增强算法

2.1受 Retinex 启发的展开与合作先验架构搜索的弱光图像增强

原文：《Retinex-inspired Unrolling with Cooperative Prior Architecture Search
for Low-light Image Enhancement》

：https://arxiv.org/pdf/2012.05609v1.pdf

这篇文章借鉴了Retinex的思想，用一个CNN来代替传统Retinex里的光照图估计。

 图一 传统Retinex结构图

 图二 用CNN网络代替传统光照图估计模块

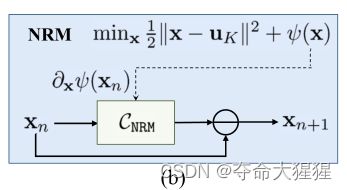
又借鉴了这样的思想设计了一个去噪模块。

图三 去噪模块

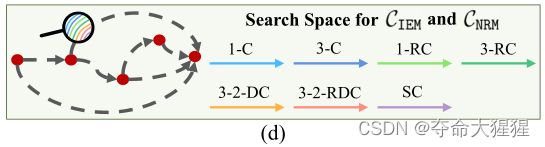
CNN网络的示意图如下图所示 。候选操作包括 1×1 和 3×3 卷积（1-C 和 3-C），1×1 和 3×3 残差卷积（1-RC 和 3-RC），3×3 扩张卷积，扩张率为2 (3-2-DC)，3×3 Residual Dilation Convolution with dilation rate of 2 (3-2-RDC), and Skip Connection (SC)。

 图四 CNN网络

整体网络结构：

Network(
  (_criterion): LossFunction(
    (l2_loss): MSELoss()
    (smooth_loss): SmoothLoss()
  )
  (_denoise_criterion): DenoiseLossFunction(
    (l2_loss): MSELoss()
    (smooth_loss): SmoothLoss()
    (tv_loss): TVLoss()
  )
  (enhance_net): EnhanceNetwork(
    (iems): ModuleList(
      (0): IEM(
        (cell): SearchBlock(
          (c1_d): Identity()
          (c1_r): ResBlock(
            (op): Conv2d(3, 3, kernel_size=(1, 1), stride=(1, 1))
          )
          (c2_d): ResBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(2, 2), dilation=(2, 2))
          )
          (c2_r): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (c3_d): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (c3_r): Identity()
          (c4): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (act): LeakyReLU(negative_slope=0.05)
          (c5): Conv2d(12, 3, kernel_size=(1, 1), stride=(1, 1))
        )
        (activate): Sigmoid()
      )
      (1): IEM(
        (cell): SearchBlock(
          (c1_d): Identity()
          (c1_r): ResBlock(
            (op): Conv2d(3, 3, kernel_size=(1, 1), stride=(1, 1))
          )
          (c2_d): ResBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(2, 2), dilation=(2, 2))
          )
          (c2_r): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (c3_d): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (c3_r): Identity()
          (c4): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (act): LeakyReLU(negative_slope=0.05)
          (c5): Conv2d(12, 3, kernel_size=(1, 1), stride=(1, 1))
        )
        (activate): Sigmoid()
      )
      (2): IEM(
        (cell): SearchBlock(
          (c1_d): Identity()
          (c1_r): ResBlock(
            (op): Conv2d(3, 3, kernel_size=(1, 1), stride=(1, 1))
          )
          (c2_d): ResBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(2, 2), dilation=(2, 2))
          )
          (c2_r): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (c3_d): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (c3_r): Identity()
          (c4): ConvBlock(
            (op): Conv2d(3, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          )
          (act): LeakyReLU(negative_slope=0.05)
          (c5): Conv2d(12, 3, kernel_size=(1, 1), stride=(1, 1))
        )
        (activate): Sigmoid()
      )
    )
  )
  (denoise_net): DenoiseNetwork(
    (stem): Conv2d(3, 6, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (nrms): ModuleList(
      (0): SearchBlock(
        (c1_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c1_r): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c2_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(3, 3), stride=(1, 1), padding=(2, 2), dilation=(2, 2))
        )
        (c2_r): Identity()
        (c3_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c3_r): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c4): Identity()
        (act): LeakyReLU(negative_slope=0.05)
        (c5): Conv2d(24, 6, kernel_size=(1, 1), stride=(1, 1))
      )
      (1): SearchBlock(
        (c1_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c1_r): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c2_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(3, 3), stride=(1, 1), padding=(2, 2), dilation=(2, 2))
        )
        (c2_r): Identity()
        (c3_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c3_r): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c4): Identity()
        (act): LeakyReLU(negative_slope=0.05)
        (c5): Conv2d(24, 6, kernel_size=(1, 1), stride=(1, 1))
      )
      (2): SearchBlock(
        (c1_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c1_r): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c2_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(3, 3), stride=(1, 1), padding=(2, 2), dilation=(2, 2))
        )
        (c2_r): Identity()
        (c3_d): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c3_r): ResBlock(
          (op): Conv2d(6, 6, kernel_size=(1, 1), stride=(1, 1))
        )
        (c4): Identity()
        (act): LeakyReLU(negative_slope=0.05)
        (c5): Conv2d(24, 6, kernel_size=(1, 1), stride=(1, 1))
      )
    )
    (activate): Sequential(
      (0): Conv2d(6, 3, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    )
  )
)

2.2双边直方图均衡化

相关论文：'BILATERAL HISTOGRAM EQUALIZATION FOR X-RAY IMAGE TONE MAPPING'

：Bilateral Histogram Equalization for X-Ray Image Tone Mapping | IEEE Conference Publication | IEEE Xplore

参考文献：

————————————————
版权声明：Retinex部分为CSDN博主「伊利亚瑟」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_42985978/article/details/127035841

———————————————
版权声明：本文为CSDN博主「桂哥317」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_15971883/article/details/88699218