Leetcode每日一题：1782. 统计点对的数目（2023.8.24 C++）

目录

1782. 统计点对的数目

题目描述：

实现代码与解析：

hash + 双指针

原理思路：

---

1782. 统计点对的数目

题目描述：

        给你一个无向图，无向图由整数 n  ，表示图中节点的数目，和 edges 组成，其中 edges[i] = [ui, vi] 表示 ui 和 vi 之间有一条无向边。同时给你一个代表查询的整数数组 queries 。

第 j 个查询的答案是满足如下条件的点对 (a, b) 的数目：

• a < b
• cnt 是与 a 或者 b 相连的边的数目，且 cnt 严格大于 queries[j] 。

请你返回一个数组 answers ，其中 answers.length == queries.length 且 answers[j] 是第 j 个查询的答案。

请注意，图中可能会有 多重边 。

示例 1：

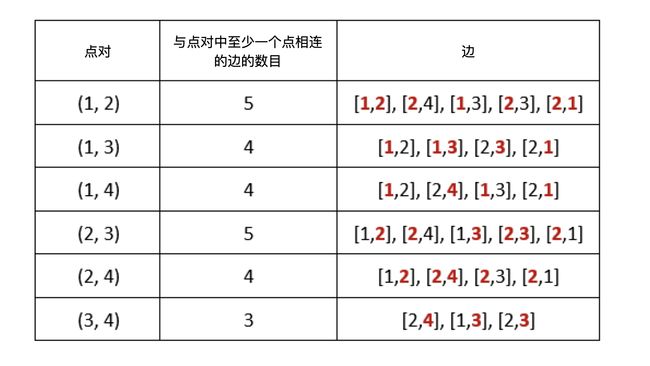
输入：n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
输出：[6,5]
解释：每个点对中，与至少一个点相连的边的数目如上图所示。
answers[0] = 6。所有的点对(a, b)中边数和都大于2，故有6个；
answers[1] = 5。所有的点对(a, b)中除了(3,4)边数等于3，其它点对边数和都大于3，故有5个。

示例 2：

输入：n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
输出：[10,10,9,8,6]

提示：

• 2 <= n <= 2 * 104
• 1 <= edges.length <= 105
• 1 <= ui, vi <= n
• ui != vi
• 1 <= queries.length <= 20
• 0 <= queries[j] < edges.length

实现代码与解析：

hash + 双指针

class Solution {
public:
    vector countPairs(int n, vector>& edges, vector& queries) {
        
        vector deg(n); // 每个节点的度 1 ~ n
        unordered_map rpt; // 重复计算的边

        // 算度，hash记边
        for (int i = 0; i < edges.size(); i++)
        {
            int a = edges[i][0] - 1, b = edges[i][1] - 1;
            if (a > b) swap(a, b);
            deg[a]++;
            deg[b]++;
            rpt[a << 16 | b]++; // 相当于两个hash，ab边转换，以及对应个数 
        }

        vector arr = deg;
        sort(arr.begin(), arr.end());
        vector res;

        for (int i = 0; i < queries.size(); i++)
        {
            int bound = queries[i];
            int sum = 0;

            // 双指针r找的是第二个数的左边界，因为右边界已经确定是n-1，不用再找了，别搞错了
            for (int l = 0, r = n - 1; l < n; l++ ) 
            {
                while(l < r && arr[l] + arr[r] > bound) r--;
                sum += n - 1 - max(l, r);
            }

            // 去重复
            for (auto &[rp, cnt]: rpt)
            {
                int a = rp >> 16, b = rp & 0xffff;
                if (deg[a] + deg[b] > bound && deg[a] + deg[b] - cnt <= bound) sum--;
            }
            res.push_back(sum);
        }
        return res;
    }
};

原理思路：

        1、存下每个节点的度。

        2、记录每条边，并且记录重边个数。

rpt[a << 16 | b]++;

这种写法，可以将a、b哈希后，记录对应值。

        解析此哈希的方法在去重的代码中，就是逆向思维即可。

        3、将点的度排序。

        4、遍历询问，双指针 l 从最小值开始遍历，r 找出与其和大于等于询问的范围的左边界。差值， n - 1 - max(l, r) 就是符合条件的对数，因为 r 可能小于 l 为了避免重复计算，要取个max，当然，此时还没考虑重边的去除计算。  

        5、遍历边，若在去重前，两边端点节点度和大于目标值，说明已经被sum计算，若去重后，不在符合条件，将sum减一，去掉这种情况。 

        最后返回答案即可。