权重初始化
常用的权重初始化方法:
随机初始化(Random Initialization)
Xavier 初始化(Glorot Initialization)
He 初始化(He Initialization)Kaiming
零初始化(Zero Initialization)
预训练初始化(Pre-trained Initialization):从预训练的模型中加载权重作为初始化,例如从在大型数据集上预训练的模型中加载权重,然后进行微调。
自定义初始化(Custom Initialization):根据特定的问题领域和网络架构,设计适合的权重初始化策略。
为什么要进行权重初始化设计:从梯度消失与爆炸说起
-
要避免梯度消失或者梯度爆炸,就要严格控制网络输出层的输出值的范围,也就是每一层网络的输出值不能太大也不能太小。
-
只要采用恰当的权值初始化方法,就可以实现网络的输出值的尺度维持在一定范围内, 这样在反向传播的时候,就有利于缓解梯度消失或者爆炸现象的发生
但是与方差有什么关系
在实际中我们还得考虑激活函数的存在,从上面的前向传播中加一个激活函数再看一下结果
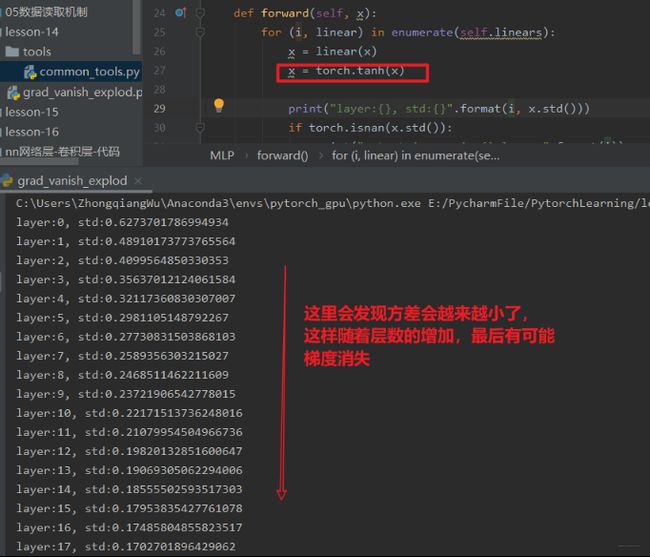
具有激活函数的时候,怎么对权重进行初始化呢?
Xavier初始化
方差一致性:保持数据尺度范围维持在恰当范围, 通常方差为1。 如果有了激活函数之后,我们应该怎么对权重初始化呢?
2010年Xavier发表了一篇文章,详细探讨了如果有激活函数的时候,如何进行权重初始化, 当然它也是运用的方差一致性原则, 但是它这里考虑的是饱和激活函数, 如sigmoid, tanh。
我们在参数初始化里面用Xavier初始化权重
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
# Xavier初始化权重
tanh_gain = nn.init.calculate_gain('tanh') #计算激活函数的方差变化尺度
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)
这里面用到了一个函数nn.init.calculate_gain(nonlinearity, param=None)这个函数的作用是计算激活函数的方差变化尺度, 怎么理解这个方差变化尺度呢?其实就是输入数据的方差除以经过激活函数之后的输出数据的方差。nonlinearity表示激活函数的名称,如tanh, param表示激活函数的参数,如Leaky ReLU的negative_slop。 (这里不用也行,但得知道这个方法)。这时候再来看一下最后的结果:
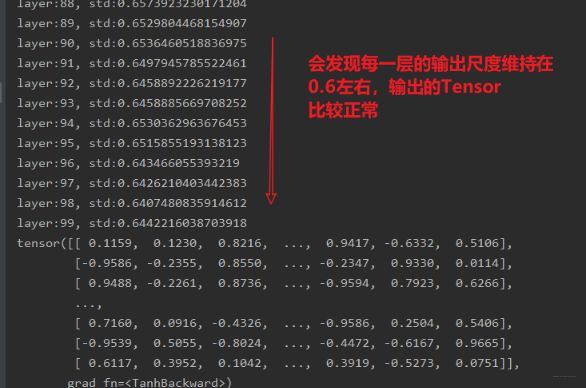
所以Xavier权重初始化,有利于缓解带有sigmoid,tanh的这样的饱和激活函数的神经网络的梯度消失和爆炸现象。
Kaiming初始化
这个依然是考虑的方差一致性原则,针对的激活函数是ReLU及其变种
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.kaiming_normal_(m.weight.data)
# nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num)) # 这两句话其实作用一样,不过自己写还得计算出标准差
十种权重初始化方法
Pytorch里面提供了很多权重初始化的方法,可以分为下面的四大类:
针对饱和激活函数(sigmoid, tanh):Xavier均匀分布, Xavier正态分布
针对非饱和激活函数(relu及变种):Kaiming均匀分布, Kaiming正态分布
三个常用的分布初始化方法:均匀分布,正态分布,常数分布
三个特殊的矩阵初始化方法:正交矩阵初始化,单位矩阵初始化,稀疏矩阵初始化:
总结
方差要维持在一定范围之内,不然可能出现梯度爆炸或者消失的情况。由于加上激活函数后,所以要选择适合该激活函数的权重初始化方法
系统学习Pytorch笔记六:模型的权值初始化与损失函数介绍
权重初始化
