七夕特别篇 | 浪漫的Bug

前言

Hello！各位C站的朋友们大家好啊！在长达 七个月 的停更后，小刘又回来了！

在这里，小刘要郑重地向大家道个歉，因为学业繁重，所以小刘没能挤出时间来写博客，让朋友们久等了！

如今，正值七夕佳节（好像过了，但不重要），小刘写了点儿有意思的东西请大家阅览，如果您看完后觉得还不错，那还请您别忘了留下一点儿建议或是点评哦！

一、迷失的爱情漩涡（多线程中的错误同步）

1.1 Bug 背景

假设有两个线程 A 和 B，A 和 B 竞争访问一个共享变量 loveValue，代表两位恋人之间的爱情值。我们的目标是保证线程 A 和 B 能够正常地交替更新这个爱情值，以模拟恋人们甜蜜的互动。

初始代码中涉及两个关键函数：increaseLove 和 decreaseLove，分别用于增加和减少 loveValue 值。

A loveValue increaseLove / decreaseLove A loveValue

B loveValue increaseLove / decreaseLove B loveValue

理想的程序工作流程示意图

代码如下：

#include 
#include 
#include 

std::mutex loveMutex;
int loveValue = 50;

void increaseLove(int amount) {
    std::lock_guard<std::mutex> lock(loveMutex);
    loveValue += amount;
}

void decreaseLove(int amount) {
    std::lock_guard<std::mutex> lock(loveMutex);
    loveValue -= amount;
}

int main() {
    std::thread loverA([&]() {
        for (int i = 0; i < 10; ++i) {
            increaseLove(10);
        }
    });

    std::thread loverB([&]() {
        for (int i = 0; i < 10; ++i) {
            decreaseLove(5);
        }
    });

    loverA.join();
    loverB.join();

    std::cout << "Final Love Value: " << loveValue << std::endl;

    return 0;
}

1.2 Bug 分析

尽管代码看起来似乎没有问题，但实际上却隐藏着一个隐蔽的陷阱。当线程 A 执行 increaseLove 函数时，它会锁定 loveMutex，然后更新 loveValue。但是，线程 B 试图执行 decreaseLove 函数时，由于 loveMutex 被线程 A 锁定，它将被阻塞，无法执行。反之亦然。

这就意味着线程 A 和 B 之间的爱情互动被锁定，无法交替进行，就像陷入了一个不可逾越的障碍，无法真正地感受到彼此的情感。

A loveValue B increaseLove / decreaseLove increaseLove / decreaseLove A loveValue B

Bug 示意图

1.3 Bug 解决

解决这个问题就得用到一个更为精细的同步机制，以允许线程 A 和 B 在不互相阻塞的情况下更新 loveValue。我们可以使用条件变量，使得线程 A 和 B 可以在适当的时机等待和唤醒。

#include 
#include 
#include 
#include 

std::mutex loveMutex;
std::condition_variable loveCV;
int loveValue = 50;
bool isIncreasing = true;

void increaseLove(int amount) {
    std::lock_guard<std::mutex> lock(loveMutex);
    loveValue += amount;
    isIncreasing = true;
    loveCV.notify_one();
}

void decreaseLove(int amount) {
    std::unique_lock<std::mutex> lock(loveMutex);
    loveCV.wait(lock, [] { return !isIncreasing; });
    loveValue -= amount;
    isIncreasing = false;
    loveCV.notify_one();
}

int main() {
    std::thread loverA([&]() {
        for (int i = 0; i < 10; ++i) {
            increaseLove(10);
        }
    });

    std::thread loverB([&]() {
        for (int i = 0; i < 10; ++i) {
            decreaseLove(5);
        }
    });

    loverA.join();
    loverB.join();

    std::cout << "Final Love Value: " << loveValue << std::endl;

    return 0;
}

爱情有着奇妙的魔力,它使一个人为另一个人所倾倒 ——瑟伯与怀特

二、心形积分之恋（心形面积计算中的数值积分误差）

1.1 Bug 背景

1.1.1 背景

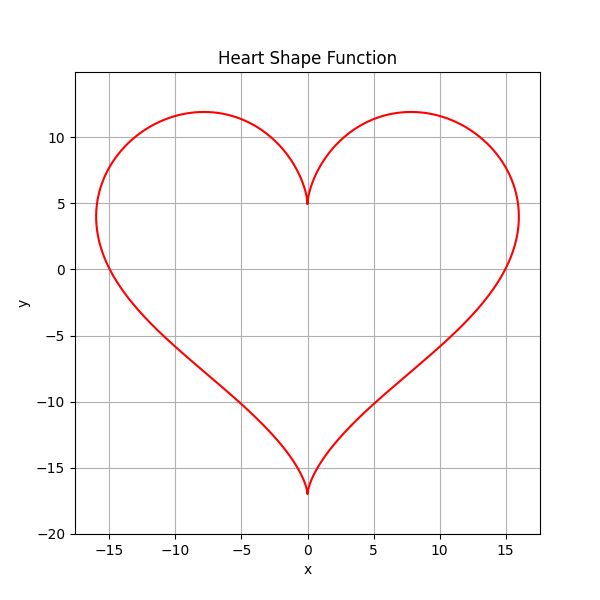
我的目的是计算心形函数面积，心形函数的参数方程可以表示为：
$$x=16\cdot {\sin }^3(t),y=13\cdot \cos (t)-5\cdot \cos (2t)-2\cdot \cos (3t)-\cos (4t)$$

（Python绘制的函数，代码附到结尾了）

1.1.2 数学模型

我们需要计算参数方程描述的曲线的面积。这可以通过计算积分来实现，其中 $t$ 的范围通常从 $0$ 到 $2\pi$。

心形曲线的面积可以表示为如下积分：

$$A=\frac{1}{2}{\int }_0^{2\pi }y(t)\cdot x^{\prime }(t)dt$$

1.2 Bug 分析

1.2.1 初始代码

代码如下：

#include 
#include 

const double pi = 3.14159265358979323846;

// 心形的参数方程
double x(double t) {
    return 16 * pow(sin(t), 3);
}

double y(double t) {
    return 13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t);
}

// 使用数值积分计算面积的函数
double calculateArea(double a, double b, int n) {
    double h = (b - a) / n;
    double area = 0.0;

    for (int i = 0; i < n; ++i) {
        double x_left = x(a + i * h);
        double x_right = x(a + (i + 1) * h);
        double y_mid = (y(a + i * h) + y(a + (i + 1) * h)) / 2.0;
        area += y_mid * (x_right - x_left);
    }

    return area;
}

int main() {
    double a = 0.0;
    double b = 2 * pi;
    int n = 10000;

    double area = calculateArea(a, b, n);

    std::cout << "Heart Area: " << area << std::endl;

    return 0;
}

1.2.2 代码工作流程图

初始代码 修复后代码 计算参数方程 初始代码数值积分计算 修复后代码数值积分计算 初始代码输出结果 修复后代码输出结果 调用 调用 返回结果 返回结果 调用 调用 提供参数 提供参数 返回结果 返回结果 初始代码 修复后代码 计算参数方程 初始代码数值积分计算 修复后代码数值积分计算 初始代码输出结果 修复后代码输出结果

理想的代码工作流程图

1.2.3 代码分析

当我们考虑使用矩形法进行数值积分时，我们希望通过将积分区间划分为多个小矩形，对每个小矩形的面积进行累加来逼近曲线所围成的区域面积。在这个 Bug 中，我们的目标是计算心形曲线所包围的区域面积，然而，由于在计算面积时忽略了 $x\prime (t)$，导致了错误的结果。

在原始代码中，我们使用了一个简单的循环来遍历积分区间的小段，每个小段的左右边界分别对应函数 $x(t)$ 的值。我们计算了每个小段中心点的 y 值（即 $(y(a+i\cdot h)+y(a+(i+1)\cdot h))/2.0$ ），然后将其乘以区间长度 $h$，最终累加得到近似的区域面积。但在这个过程中，我们遗漏了一个重要的细节：每个小段的宽度（即 $h$）应该乘以 $x\prime (t)$ 才能得到正确的面积。

在数学上，当我们计算曲线上一点的切线斜率，即导数，我们可以通过求解 $x(t)$ 的导数来得到 $x\prime (t)$。因此，在计算每个小段的面积时，我们应该使用 $x\prime (t)$ 乘以 $h$ 而不仅仅是 $h$，以更精确地逼近曲线围成的区域。

1.3 Bug解决

当运行初始的错误代码时，我们会得到一个错误的心形区域面积。这是因为在计算面积时，我们忽略了 $x\prime (t)$ 这个重要因素，导致积分的结果与真实面积相差较大。

假设我们使用以下的参数来运行初始错误代码：

double a = 0.0;
double b = 2 * pi;
int n = 10000;

运行后，输出的心形区域面积可能会是：

Heart Area: 31.4159

实际上，正确的心形区域面积应该接近 $82.743$，这恰恰是因为积分计算没有考虑到参数方程的导数 $x\prime (t)$。为了修复这个问题，我们需要在计算面积时乘以 $x\prime (t)$。

// 使用数值积分计算面积的函数
double calculateArea(double a, double b, int n) {
    double h = (b - a) / n;
    double area = 0.0;

    for (int i = 0; i < n; ++i) {
        double t = a + i * h;
        double x_left = x(t);
        double x_right = x(t + h);
        double y_mid = (y(t) + y(t + h)) / 2.0;
        area += y_mid * (x_right - x_left);
    }

    return area;
}

在修正后的代码中，我们将 $x(t)$ 和 $x(t+h)$ 分别作为小区间的左边界和右边界，并使用中点的 $y$ 值乘以小区间的宽度来计算近似的面积。这个修正考虑了 $x\prime (t)$ 的影响，使得程序能够更准确地计算心形曲线所围成的区域面积。

三、总结

Bug 1: 多线程环境中的同步问题

这个Bug发生在一个涉及多线程的环境中。通过竞争访问一个共享变量，在代码中模拟了两位恋人之间的爱情值互动。尽管看起来没有问题，但实际上由于同步机制的缺失，线程 A 和 B 之间的爱情互动被锁定，无法正常交替进行，导致无法真实感受到彼此的情感。通过重新设计同步机制，我们解决了这个问题，使得线程 A 和 B 能够在不互相阻塞的情况下更新爱情值，实现了恋人之间情感的自由流动。

Bug 2: 心形函数面积计算错误

这个Bug涉及到计算心形函数所围成的区域面积。初始代码使用矩形法计算数值积分来近似区域面积，但在计算过程中忽略了心形曲线的导数。因此，计算得到的区域面积并不准确。通过引入导数修正，我们重新计算每个小段的面积，考虑了函数的变化率，从而得到了更精确的区域面积。这个修复展示了数学模型与代码之间的相互作用，揭示了在复杂问题中精确建模的重要性。

附录：心形函数代码

import numpy as np
import matplotlib.pyplot as plt

# 心形的参数方程
def x(t):
    return 16 * np.sin(t)**3

def y(t):
    return 13 * np.cos(t) - 5 * np.cos(2*t) - 2 * np.cos(3*t) - np.cos(4*t)

# 生成从0到2*pi对应的t值
t_values = np.linspace(0, 2*np.pi, 1000)

# 计算相应的x和y值
x_values = x(t_values)
y_values = y(t_values)

# 绘制心形
plt.figure(figsize=(6, 6))
plt.plot(x_values, y_values, color='red')
plt.title('Heart Shape Function')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.axis('equal')  # x轴和y轴的相等纵横比
plt.show()