时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)
时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)
目录
-
- 时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)
-
- 预测效果
- 基本介绍
- 模型介绍
- 程序设计
- 参考资料
- 致谢
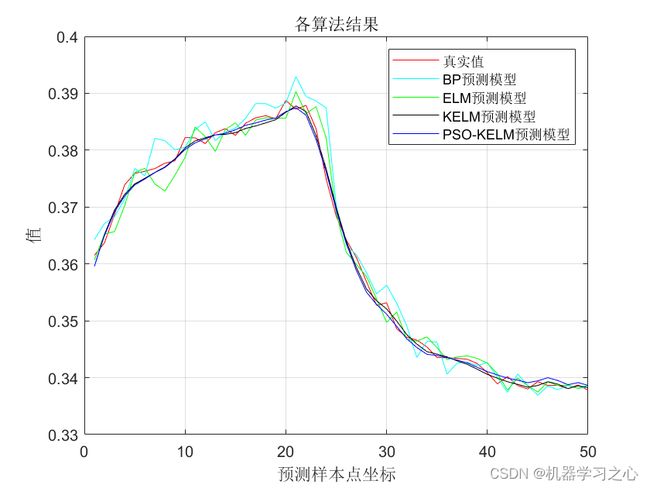
预测效果
基本介绍
MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)(完整源码和数据)
模型介绍
PSO-KELM,常用于时间序列预测任务。
PSO是一种基于群体智能的优化算法,它模拟了鸟群觅食的行为。在PSO中,每个个体被称为粒子,代表了解空间中的一个候选解。粒子通过在解空间中搜索来寻找最优解,同时根据个体最优和全局最优的信息进行调整和更新。PSO算法通过迭代更新粒子的位置和速度来逐步优化解的质量。
PSO-KELM的时间序列预测步骤如下:
准备时间序列数据集,将其划分为训练集和测试集。
初始化PSO算法的粒子群,并随机初始化粒子的位置和速度。
对于每个粒子,使用KELM算法,其中隐藏层的连接权重和偏置通过PSO进行优化。
根据训练得到的模型,对测试集进行预测。
评估预测结果的准确性。
根据预测准确性和PSO的优化目标,更新粒子的速度和位置。
重复步骤3至步骤6,直到达到预定的迭代次数或满足停止准则。
根据最优的粒子位置得到最终的连接权重和偏置,用于进行时间序列的预测。
需要注意的是,PSO-KELM算法的性能和结果可能会受到参数设置的影响,例如粒子数、迭代次数、网络的隐藏层节点数等。因此,在实际应用中需要根据具体问题进行调优和参数选择。
程序设计
- 完整程序和数据下载地址方式:私信博主回复MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比。
%% 各算法对比
clc;clear;close all
%%
Positions = initialization(SearchAgents_no, dim, ub, lb);
%% 用于记录迭代曲线
Convergence_curve = zeros(1, Max_iteration);
%% 循环计数器
iter = 0;
%% 优化算法主循环
while iter < Max_iteration % 对迭代次数循环
for i = 1 : size(Positions, 1) % 遍历
Flag4ub = Positions(i, :) > ub;
Flag4lb = Positions(i, :) < lb;
% 若的位置在最大值和最小值之间,则位置不需要调整,若超出最大值,最回到最大值边界
% 若超出最小值,最回答最小值边界
Positions(i, :) = (Positions(i, :) .* (~(Flag4ub + Flag4lb))) + ub .* Flag4ub + lb .* Flag4lb;
% 计算适应度函数值
% Positions(i, 2) = round(Positions(i, 2));
% fitness = fical(Positions(i, :));
fitness = fobj(Positions(i, :));
% 更新 Alpha, Beta, Delta
if fitness < Alpha_score % 如果目标函数值小
if fitness > Alpha_score && fitness > Beta_score &&
Delta_score = fitness; % 则将Delta的目标函数值更新为最优目标函数值
Delta_pos = Positions(i, :); % 同时更新Delta的位置
end
end
% 线性权重递减
wa = 2 - iter * ((2) / Max_iteration);
% 更新搜索群的位置
for i = 1 : size(Positions, 1) % 遍历每个
for j = 1 : size(Positions, 2) % 遍历每个维度
% 包围猎物,位置更新
r1 = rand; % r1 is a random number in [0,1]
r2 = rand; % r2 is a random number in [0,1]
A1 = 2 * wa * r1 - wa; % 计算系数A,Equation (3.3)
C1 = 2 * r2; % 计算系数C,Equation (3.4)
% Alpha 位置更新
D_alpha = abs(C1 * Alpha_pos(j) - Positions(i, j)); % Equation (3.5)-part 1
X1 = Alpha_pos(j) - A1 * D_alpha; % Equation (3.6)-part 1
r1 = rand; % r1 is a random number in [0,1]
r2 = rand; % r2 is a random number in [0,1]
A2 = 2 * wa * r1 - wa; % 计算系数A,Equation (3.3)
C2 = 2 *r2; % 计算系数C,Equation (3.4)
% Beta 位置更新
D_beta = abs(C2 * Beta_pos(j) - Positions(i, j)); % Equation (3.5)-part 2
X2 = Beta_pos(j) - A2 * D_beta; % Equation (3.6)-part 2
r1 = rand; % r1 is a random number in [0,1]
r2 = rand; % r2 is a random number in [0,1]
A3 = 2 *wa * r1 - wa; % 计算系数A,Equation (3.3)
C3 = 2 *r2; % 计算系数C,Equation (3.4)
% Delta 位置更新
D_delta = abs(C3 * Delta_pos(j) - Positions(i, j)); % Equation (3.5)-part 3
X3 = Delta_pos(j) - A3 * D_delta; % Equation (3.5)-part 3
% 位置更新
Positions(i, j) = (X1 + X2 + X3) / 3; % Equation (3.7)
end
end
% 更新迭代器
iter = iter + 1;
Convergence_curve(iter) = Alpha_score;
curve(iter)=sum(Convergence_curve)/iter;
disp(['第',num2str(iter),'次迭代'])
disp(['current iteration is: ',num2str(iter), ', best fitness is: ', num2str(Alpha_score)]);
end
%% 记录最佳参数
% best_lr = Alpha_pos(1, 1);
% best_hd = Alpha_pos(1, 2);
% best_l2 = Alpha_pos(1, 3);
end
function result(true_value,predict_value,type)
disp(type)
rmse=sqrt(mean((true_value-predict_value).^2));
disp(['根均方差(RMSE):',num2str(rmse)])
mae=mean(abs(true_value-predict_value));
disp(['平均绝对误差(MAE):',num2str(mae)])
mape=mean(abs((true_value-predict_value)./true_value));
disp(['平均相对百分误差(MAPE):',num2str(mape*100),'%'])
r2 = R2(predict_value, true_value);
disp(['R平方决定系数(MAPE):',num2str(r2)])
nse = NSE(predict_value, true_value);
disp(['纳什系数(NSE):',num2str(nse)])
fprintf('\n')
参考资料
[1] https://blog.csdn.net/kjm13182345320?spm=1010.2135.3001.5343
[2] https://mianbaoduo.com/o/bread/mbd-YpiamZpq
[3] SI Y W,YIN J. OBST-based segmentation approach to financial time series[J]. Engineering Applications of Artificial Intelligence,2013,26( 10) : 2581-2596.
[4] YUAN X,CHEN C,JIANG M,et al. Prediction Interval of Wind Power Using Parameter Optimized Beta Distribution Based LSTM Model[J]. Applied Soft Computing,2019,82:105550.143
致谢
- 大家的支持是我写作的动力!
- 感谢大家订阅,记得备注!