非标准分布随机数生成 - 逆变换ITM与舍选法Rejection

统计学 - 非标准分布随机数生成

最近做了几道有关随机数生成的实验，记录下来写个总结吧，其中核心证明略。
—— 2020.3.24： 20:50

首先明白一些概念，这里随机数是指服从某种分布的随机变量，比如高斯(标准正态)分布 X~U(0,1)。如果已知随机变量的概率密度函数pdf，进而可以由积分得出其累积概率分布函数CDF，CDF只增不减，最大为1。
明白以上之后，我们就需要来验证或者说如何说明概率密度函数与随机变量的关系？你给我了概率密度函数f(x)，如果我知道了随机变量x的取值，那么我就可以知道这个点的概率p，但是你给了这个函数公式说是这个概率就一定是这个概率吗，怎么验证呢？
我们使用采样的方法，我们可以画出概率密度函数曲线图，对于某个概率，在多种可能的采样情况下，如果这个概率下所采集到的样本点相对总体样本点就是这个比例，这个问题不就可以直观说明了。即，某个点的概率越大，那么这个点所采集的样本数也应该越多。
那么，如何得到这些采样点呢，这便是标题所讲的随机数生成。

逆变换ITM

定理：

• 设随机变量Y的分布函数为F(y)是连续函数，而U是(0,1)上均匀分布的随机变量。另X=F^-1(U)，则X和Y具有相同的分布。

这个有什么意义呢？如果我们知道了U的分布情况，那么其反函数的分布不就是我们要求的随机数嘛。故根据反函数，随机生成U，解出对应的X，再画出X的分布情况，这个其实就是Y的概率密度函数。
但是，这个方法有个缺陷在于要求F是可逆的。
来看一道练习：

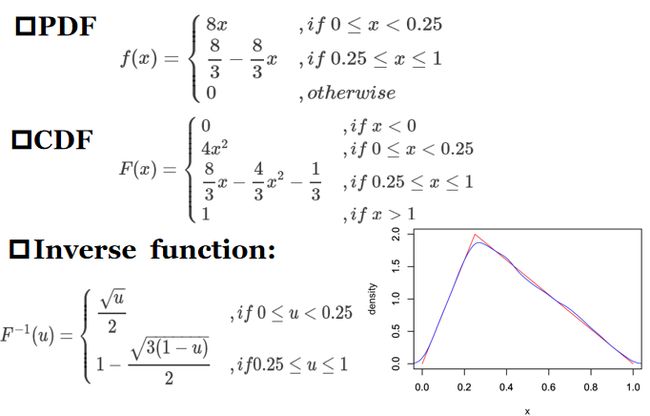
上图中红色曲线便是f(x)的概率分布曲线图，而蓝色曲线是逆变换后样本点的分布图，可以看出趋势是一致的。
代码实现

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math

def EX1_ITM(maxCnt=50000): # 逆变换随机变量，采样点可调
	X_u=[] # 用服从均匀分布的u来生成逆随机数
	for i in range(maxCnt):
		u=np.random.random() # 生成[0.0,1.0)之间的随机数
		if u>=0 and u<0.25: # 逆变换
			X_u.append(np.sqrt(u)/2)
		else:X_u.append(1-np.sqrt(3*(1-u))/2)

	StandarXaxis=np.linspace(0,1,1000)  # 原函数x的概率密度fx，概率密度越大那么逆随机数在此的采样点越多，直方图越高(注意区分概率密度f_x与概率分布F_x)
	Stand_fx=[8*x for x in StandarXaxis if x<0.25] # 原函数的概率密度函数
	Stand_fx.extend([8/3 *(1-x) for x in StandarXaxis if x >= 0.25])
	
	# plt.hist(x,bins=1000,density=True)
	sns.distplot(X_u,hist=False,kde=True) # hist可隐藏直方图
	plt.plot(StandarXaxis,Stand_fx)
	plt.show()
 EX1_ITM()

其效果图：

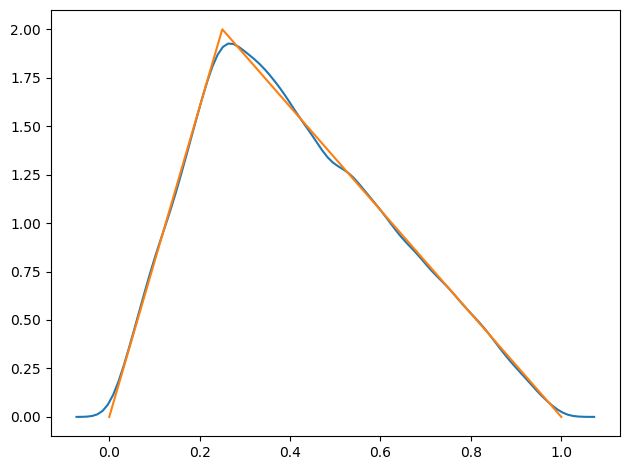
我们隐藏了直方图块，纵轴表示x的分布，用直方图会更直观些。

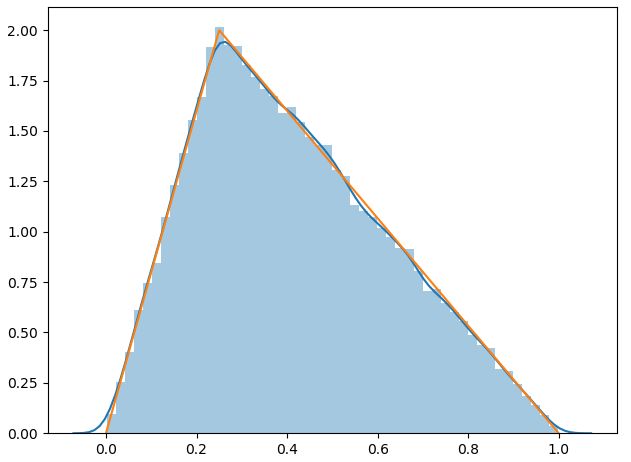
再来看另外一道练习：

还是用同样的方法，先根据CDF上限始终是1来随机生成[0.0,1.0)之间的数，然后逆变换出x，采样点数量可变。然后画出原函数即x的概率分布曲线，发现基本吻合。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
def EX2_ITM(m=0.5,maxCnt=2000):
	X_u=[]
	for i in range(maxCnt):
		u=np.random.random() # u其实就是F_x，即x的概率分布，上限始终为1
		X_u.append(np.sqrt(m*m/(1-(1-m*m)*u)))

	StandarXaxis=np.linspace(m,1.2,1000)
	X_temp=StandarXaxis**3
	Standar_hx=2*m*m/(1-m*m)/X_temp

	sns.distplot(X_u,hist=True,kde=True)
	plt.plot(StandarXaxis,Standar_hx,'r')
	plt.show()
# EX2_ITM()

效果图：

舍选法Rejection

舍选法、蒙特卡洛法、乘同余法和混合同余法。是比较常见的方法。

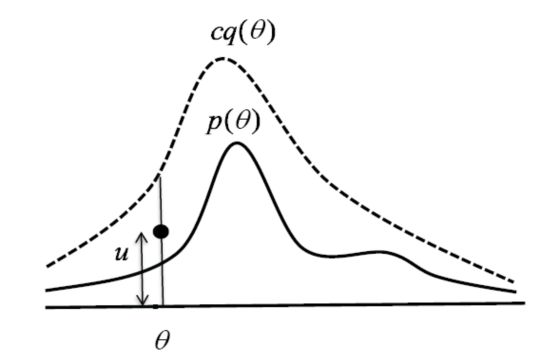
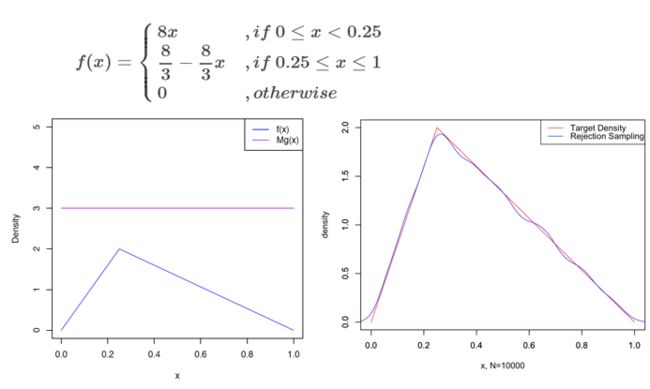
大致原理是，假设我们要验证的概率密度函数为p(θ)，那么我们找到一个常数c，和一个容易取样的函数q(θ)，使得cq>=p始终成立。然后在虚线范围内随机取若干样本点，如果这个样本点也包含在实线范围内便保留这个样本点，重复直到样本点个数足够。其计算步骤如下：

具体证明稍微复杂些，此处略过。
舍选法有两个很重要的地方：参考函数q(θ)和常数C的选择问题。
关于q，具体需要根据p(θ)，如果p是比较简单的线性函数，那么q选择常数函数即可，如果f(x)是高斯分布函数或者混合高斯分布函数，那么参考函数也选择高斯分布函数即可。常数C选择p/q的极值，这个列出不等式即可明白。

来看一道例题：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
def f_x(x):
	if x>=0 and x<0.25:return 8*x
	elif x>=0.25 and x<=1:return 8/3*(1-x)
	else:return 0

size=60000
x=np.linspace(0,1,10000)
fx=[]
for t in x: # 原函数概率密度
	fx.append(f_x(t))

M,gx=3,1

plt.figure(figsize=(18,5))
plt.subplot(121)
plt.plot(x,fx,label='f(x)')
plt.axhline(3,color='r',label='Mg(x)')
# plt.legend(loc='best')
# plt.ylim(0,5)

theta=np.random.uniform(low=0.0,high=1.0,size=size) # 均匀采样得到横轴样本点
u=np.random.uniform(low=0.0,high=M*gx,size=size) # 竖直方向采样
qz=[]
for t in theta:
	qz.append(f_x(t))

sample=theta[qz>=u] # 取舍

plt.subplot(122)
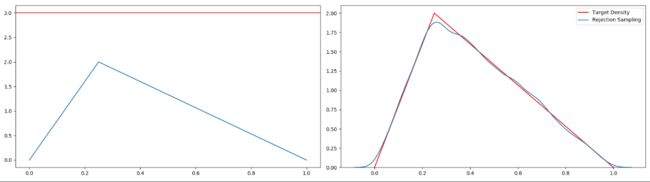
plt.plot(x,fx,color='r',label='Target Density')
sns.distplot(sample,hist=False,label='Rejection Sampling')
plt.show()

效果图：

来看另外一道练习：

这个题需要对Beta分布和gamma函数有所了解，详见后面参考文献。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math

def gamma(x):
	ans=1
	for t in range(1,x):
		ans*=t
	return ans

def f_Beta(x,a,b):
	return gamma(a+b)/gamma(a)/gamma(b) * x**(a-1) * (1-x)**(b-1)

M,gx=3,1 # 这里用正态分布更适合fx，为了方便还是用常数函数，效果稍差些
a,b=3,6 # beta分布参数
x=np.linspace(0,1,10000)
f_beta=f_Beta(x,a,b)

plt.plot(x, f_beta, 'r', label='Beta(3, 6)')

size=100000
theta=np.random.uniform(low=0.0,high=1.0,size=size)
u=np.random.uniform(low=0.0,high=M*gx,size=size)
qz=f_Beta(theta,a,b)

sample=theta[qz>=u] # 取舍
sns.distplot(sample,bins=100,hist=True,kde=True,label='Rejection Sampling')
plt.legend(loc='best')
plt.show()

效果图：

舍选法存在一个问题是C和q的选择问题容易造成较大的浪费，降低效率。比如上面我们用的事常数函数，虽然能完全包含住目标函数，但是q和p之间存在较大的空间造成浪费，采样过程就更漫长。为了解决这个问题提出了自适应舍选法。

自使用舍选法

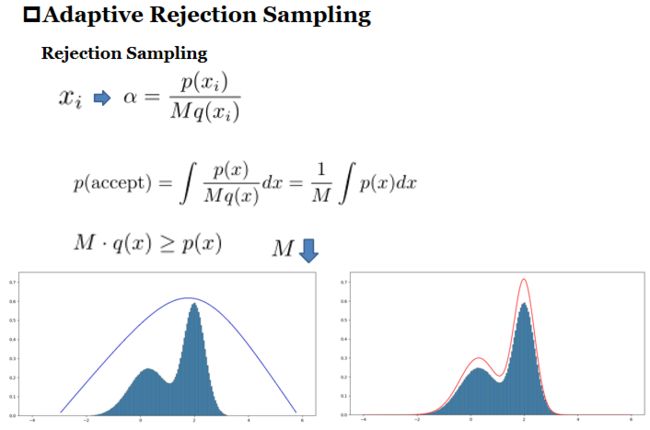
如上图，左边明显效果过低，如何变换成右边形式呢，我们需要了解一个凸函数理论。

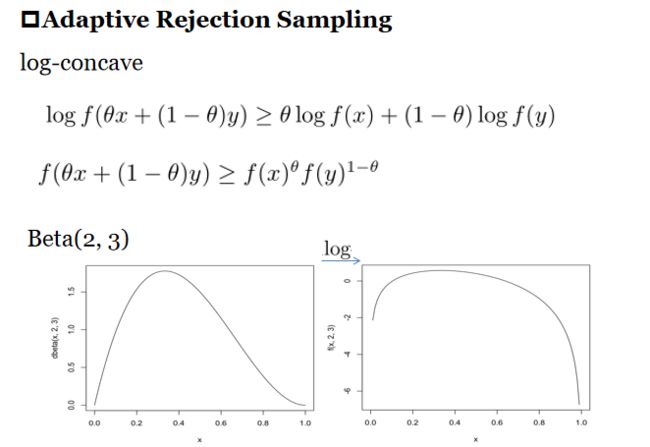
如上图，左边的Beta分布函数通过log变换可以变成右边的形式。那么，我们在右边图中取若干个点做切线，这些切线交点是可以完全包含住原函数的。反过来，我们将切线通过exp的指数变换，可以在Beta分布图中得到若干曲线图，这些曲线图的交点也可以最大化的包含住贝尔分布图。

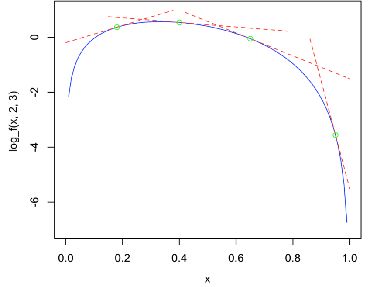
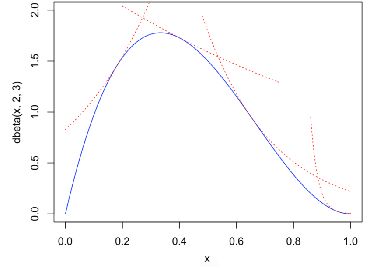
Python实现：

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

def gamma(x):
    ans = 1
    for i in range(1, x):
        ans *= i
    return ans

def beta(x, m, n):
    return gamma(m+n) / (gamma(m)*gamma(n)) * x**(m-1) * (1-x)**(n-1)

def log_f(x, m, n):
    return np.log(12) + (m-1)*np.log(x) + (n-1)*np.log(1-x)

def derivative(x, m, n):
    return (m-1)/x - (n-1)/(1-x)
m, n =2, 3
x = np.linspace(0, 1, 1000)  # 生成0到1之间，样本数为1000的等差数列
y_beta = beta(x, m, n)
#plt.plot(x, y_beta, 'r', label='dbeta(2, 3)')
#plt.show()

y_log = log_f(x, m, n)
plt.plot(x, y_log, 'b', label='log_f(2, 3)')

x_log = np.array([0.18, 0.40, 0.65, 0.95])
x = np.array([np.linspace(0, 0.35, 11), np.linspace(0.18, 0.65, 11),
              np.linspace(0.45, 0.95, 11), np.linspace(0.85, 1, 11)])

for i in range(0,4):
    log_f_y = log_f(x_log[i], m, n)
    k = derivative(x_log[i], m, n)
    b = log_f_y - k * x_log[i]
    y = k*x[i] + b
    plt.scatter(x_log[i], log_f_y, color='', marker='o', edgecolors='g')
    plt.plot(x[i], y, color='r', linestyle="--")

plt.title('Adaptive Rejection Sampling')
plt.xlabel('x')
plt.ylabel('log_f(x,2,3)')
plt.show()

matlab实现：

参考资料

1. 随机数生成算法
2. 神奇的 Gamma函数
3. Beta分布深入理解
4. 概率论中PDF、PMF和CDF的区别与联系
5. 逆分布函数法生成随机数（以指数分布和双指数分布为例）