Opencv图像分割 -- GMM(高斯混合模型)方法
一、高斯混合模型
高斯混合模型(Gaussian Mixture Model)通常简称GMM,是一种业界广泛使用的聚类
法,该方法使用了高斯分布作为参数模型,并使用了期望最大(Expectation Maximization,简
EM)算法进行训练。
1. 什么是高斯分布?
高斯分布(Gaussian distribution)有时也被称为正态分布(normal distribution),是一种在
自然界大量存在的、最为常见的分布形式。
用一个简单的例子来说明。
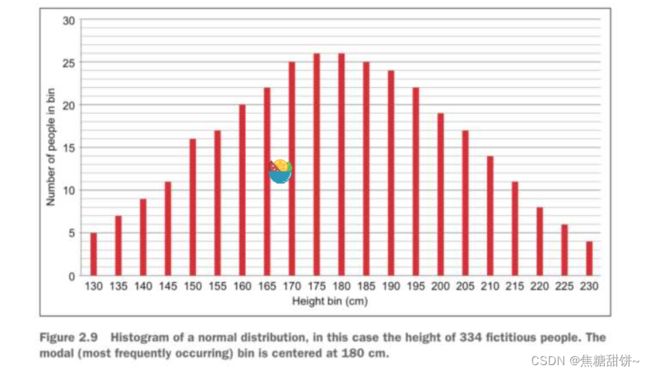
例:如果我们对大量的人口进行身高数据的随机采样,并且将采得的身高数据画成柱状图,将会得到如图1所示的图形。这张图模拟展示了334个成人的统计数据,可以看出图中最多出现的身高在180cm左右2.5cm的区间里。
图1 由334个人的身高数据构成的正态分布直方图
这个图形非常直观的展示了高斯分布的形态。
高斯分布的概率密度函数公式如下:
其中,μ表示均值,σ表示标准差。均值对应正态分布的中间位置,在本例中我们可以推测均
值在180cm附近。标准差衡量了数据围绕均值分散的程度。
正态分布的一个背景知识点是,95%的数据分布在均值周围2个标准差的范围内。本例中大约
20到30左右是标准差参数的取值,因为大多数数据都分布在120cm到240cm之间。
上面的公式是概率密度函数,也就是在已知参数的情况下,输入变量指x,可以获得相对应的
概率密度。还要注意一件事,就是在实际使用前,概率分布要先进行归一化,也就是说曲线下面的
面积之和需要为1,这样才能确保返回的概率密度在允许的取值范围内。
如果需要计算指定区间内的分布概率,则可以计算在区间首尾两个取值之间的面积的大小。
另外除了直接计算面积,还可以用更简便的方法来获得同样的结果,就是减去区间x对应的累积密
度函数(cumulative density function,CDF)。因为CDF表示的是数值小于等于x的分布概率。
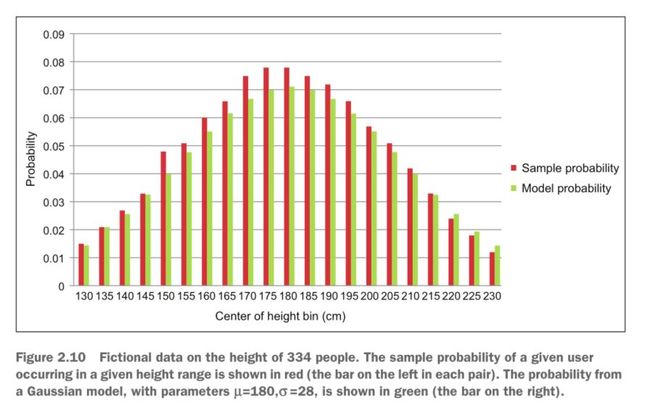
回到之前的例子来评估下参数和对应的实际数据。假设我们用柱状线来表示分布概率,每个
柱状线指相应身高值在334个人中的分布概率,用每个身高值对应的人数除以总数(334)就可以
得到对应概率值,图2用左侧的红色线(Sample Probability)来表示。
如果我们设置参数 μ =180, σ =28,使用累积密度函数来计算对应的概率值——右侧绿色线
(Model Probability),可以肉眼观察到模型拟合的精度。
图2 对给定用户,身高分布的采样概率用红色柱状图表示,高斯模型在参数μ=180,σ=28时计算出的概率用绿色柱状图表示
观察图2可以看出,刚才咱们猜测的均值参数180和标准差参数28拟合的效果很不错,虽然可
能稍微偏小了一点点。当然我们可以不断调校参数来拟合得更好些,但是更准确的办法是通过算法
来生成它们,这个过程就被称为模型训练(model training)。最常用的方法是期望最大(EM)算
法,下文会进行详细讲解。
顺便一提,采样的数据和全体数据的分布多少总是存在一定差异的。这里首先假设了采集的
334个用户的数据能代表全体人口的身高分布。另外我们还假定了隐含的数据分布是高斯分布,并
以此来绘制分布曲线,并以此为前提预估潜在的分布情况。如果采集越来越多的数据,通常身高的
分布越来越趋近于高斯(尽管仍然有其他不确定因素),模型训练的目的就是在这些假设前提下尽
可能降低不确定性。
2. 期望最大与高斯模型训练
模型的EM训练过程,直观的来讲是这样:我们通过观察采样的概率值和模型概率值的接近程
度,来判断一个模型是否拟合良好。然后我们通过调整模型以让新模型更适配采样的概率值。反复
迭代这个过程很多次,直到两个概率值非常接近时,我们停止更新并完成模型训练。
现在我们要将这个过程用算法来实现,所使用的方法是模型生成的数据来决定似然值,即通
过模型来计算数据的期望值。通过更新参数μ和σ来让期望值最大化。这个过程可以不断迭代直到
两次迭代中生成的参数变化非常小为止。该过程和k-means的算法训练过程很相似(k-means不断
更新类中心来让结果最大化),只不过在这里的高斯模型中,我们需要同时更新两个参数:分布的
均值和标准差。
3. 高斯混合模型(GMM)
高斯混合模型是对高斯模型进行简单扩展,GMM使用多个高斯分布的组合来刻画数据分布。
举例来说:想象下现在咱们不再考察全部用户的身高,而是要在模型中同时考虑男性和女性
的身高。假定之前的样本里男女都有,那么之前所画的高斯分布其实是两个高斯分布的叠加的结
果。相比只使用一个高斯来建模,现在我们可以用两个(或多个)高斯分布:
该公式和之前的公式非常相似,细节上有几点差异。首先分布概率是K个高斯分布的和,每个
高斯分布有属于自己的 μ 和 σ 参数,以及对应的权重参数,权重值必须为正数,所有权重的和必
须等于1,以确保公式给出数值是合理的概率密度值。换句话说如果我们把该公式对应的输入空间
合并起来,结果将等于1。
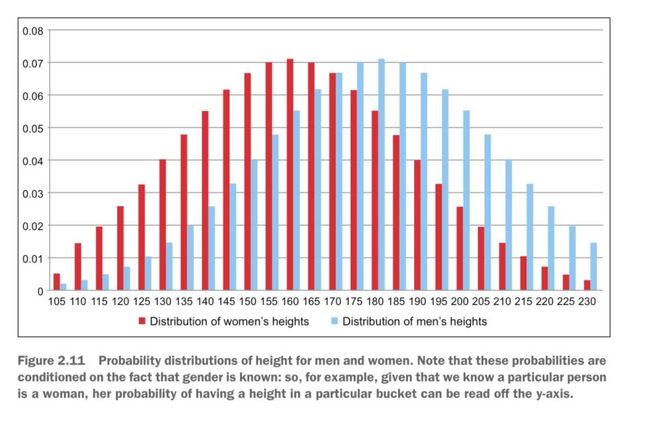
回到之前的例子,女性在身高分布上通常要比男性矮,画成图的话如图3。
图3 男性和女性身高的概率分布图
图3的y-轴所示的概率值,是在已知每个用户性别的前提下计算出来的。但通常情况下我们并
不能掌握这个信息(也许在采集数据时没记录),因此不仅要学出每种分布的参数,还需要生成性
别的划分情况( φi )。当决定期望值时,需要将权重值分别生成男性和女性的相应身高概率值并
相加。
注意,虽然现在模型更复杂了,但仍然可使用与之前相同的技术进行模型训练。在计算期望
值时(很可能通过已被混合的数据生成),只需要一个更新参数的最大化期望策略。
前面的简单例子里使用了一维高斯模型:即只有一个特征(身高)。但高斯不仅局限于一
维,很容易将均值扩展为向量,标准差扩展为协方差矩阵,用n-维高斯分布来描述多维特征。
整体来看,所有无监督机器学习算法都遵循一条简单的模式:给定一系列数据,训练出一个
能描述这些数据规律的模型(并期望潜在过程能生成数据)。训练过程通常要反复迭代,直到无法
再优化参数获得更贴合数据的模型为止。
二、Opencv中相关API
bool trainEM(InputArray samples, // 输入的样本,一个单通道的矩阵。从这个样本中,进行高斯混和模型估计。
OutputArray logLikelihoods=noArray(), //可选项,输出一个矩阵,里面包含每个样本的似然对数值。
OutputArray labels=noArray(), //可选项,输出每个样本对应的标注。
OutputArray probs=noArray()) //可选项,输出一个矩阵,里面包含每个隐性变量的后验概率补充一下EM::Types
| COV_MAT_SPHERICAL | 表示协方差矩阵是一个标量乘以单位矩阵,即sk×I,所以对协方差矩阵的估计只需要确定sk即可 |
| COV_MAT_DIAGONAL | 表示协方差矩阵是一个对角线元素为正数的对角矩阵,这时只需要对d个参数进行估计即可,d为样本特征属性的数量 |
| COV_MAT_GENERIC | 表示协方差矩阵是一个对称的正数矩阵,很显然,此时需要估计d2/2个参数,除非样本数据庞大,否则不建议设置该参数。 |
1. 数据聚类
代码:
/*
opencv中GMM方法API:
bool trainEM(InputArray samples, // 输入的样本,一个单通道的矩阵。从这个样本中,进行高斯混和模型估计。
OutputArray logLikelihoods=noArray(), //可选项,输出一个矩阵,里面包含每个样本的似然对数值。
OutputArray labels=noArray(), //可选项,输出每个样本对应的标注。
OutputArray probs=noArray()) //可选项,输出一个矩阵,里面包含每个隐性变量的后验概率
*/
#include
#include
using namespace std;
using namespace cv;
using namespace cv::ml;
int main(int argc, char** argv)
{
Mat img = Mat::zeros(500, 500, CV_8UC3);
RNG rng(12345);
//五个颜色,聚类之后的颜色随机从这里面选择
Scalar colorTab[] = {
Scalar(0,0,255),
Scalar(0,255,0),
Scalar(255,0,0),
Scalar(0,255,255), //红+绿 == 黄
Scalar(255,0,255) //蓝+红 == 粉
};
int numCluster = rng.uniform(2, 5); //随机分类总数
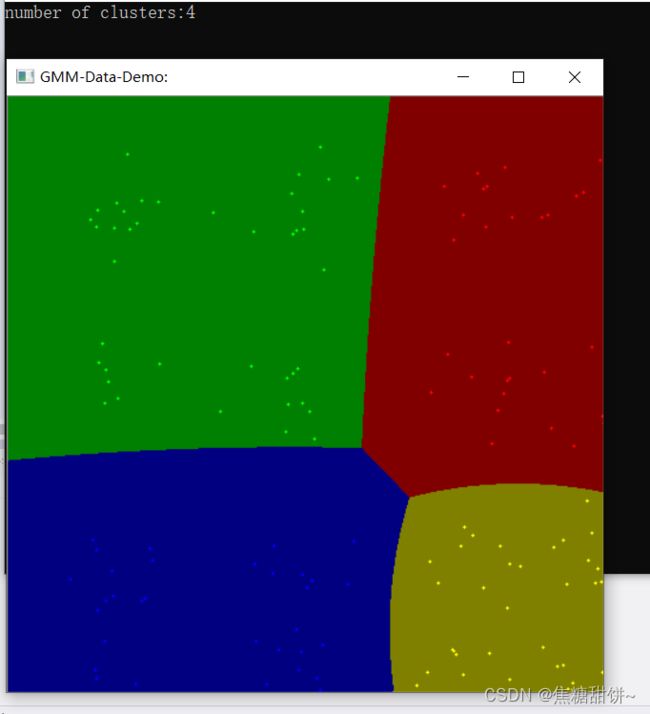
cout << "number of clusters:" << numCluster << endl;
int sampleCount = rng.uniform(5, 1000); //随机生成样本总数
//样本矩阵为points
Mat points(sampleCount, 2, CV_32FC1);
Mat labels; //存放表示每个簇的标签,是一个整数,从0开始的索引整数
//行数跟points一样,每一行中储存对应Points行数中的数据是属于哪一种的分类
Mat centers;//存放的是kmeans算法结束后每个簇的中心位置
//随机生成样本
//样本总数为sampleCount, 类别总数为numCluster
//样本矩阵为points,先按类别分成numCluster份 每一份数据的个数为sampleCount / numCluster
//然后按类别随机矩阵填充样本矩阵,第一类填充矩阵的0~sampleCount/numCluster行
//第二类填充样本矩阵的sampleCount/numCluster~(sample_count/cluster_count)*2 行,
//以此类推直到填充满所有矩阵,每一类的样本个数是一样的
for (int k = 0; k < numCluster; k++)
{
//随机出中心点
Point center;
center.x = rng.uniform(0, img.cols);
center.y = rng.uniform(0, img.rows);
// Mat.rowRange 函数从 Mat 中抽取 startrow行 到 endrow 行的数据并返回(类型与mat一致),索取的位置是左闭右开,不包含endrow
// Mat.rowRange 的返回值只是浅拷贝,指针指向还是原Mat,所以下面的 rng.fill 是对 points 的填充
//返回数组在一定跨度的行
//points为输入数组,pointChunk返回数组
//开始行为 k*sampleCount/numCluster
//结束行为 当k== numCluster - 1时 为 第sampleCount行 否则为(k + 1) * sampleCount / numCluster
//得到不同小块
Mat pointChunk = points.rowRange(k * sampleCount / numCluster,
k == numCluster - 1 ? sampleCount : (k + 1) * sampleCount / numCluster);
//用随机数对小块点进行填充
//在center坐标周围上下左右 img.cols*0.05, img.rows*0.05 的方差内生成高斯分布的随机数,最后赋值给pointChunk
rng.fill(pointChunk, RNG::NORMAL, Scalar(center.x, center.y), Scalar(img.cols*0.05, img.rows*0.05));
}
//打乱points中的顺序
randShuffle(points, 1, &rng);
Ptrem_model = EM::create();
em_model->setClustersNumber(numCluster);
em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL); //协方差矩阵类型
em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1)); //算法终止标准
em_model->trainEM(points, noArray(), labels, noArray()); //训练
//classify every image pixels;
Mat sample(1, 2, CV_32FC1);
for (int row = 0; row < img.rows; row++)
{
for (int col = 0; col < img.cols; col++)
{
sample.at(0) = (float)col;
sample.at(1) = (float)row;
//预测
//cvRound():返回跟参数最接近的整数值,即四舍五入;
//predict2返回的是double值,用cvRound进行四舍五入得到整型
//此处返回的是两个值Vec2d,取第二个值作为样本标注
int response = cvRound(em_model->predict2(sample, noArray())[1]);
Scalar c = colorTab[response];
circle(img, Point(col, row), 1, c*0.5, -1);
}
}
//draw the clusters
for (int i = 0; i < sampleCount; i++)
{
Point p(cvRound(points.at(i, 0)), points.at(i, 1));
circle(img, p, 1, colorTab[labels.at(i)], -1);
}
imshow("GMM-Data-Demo:", img);
waitKey(0);
destroyAllWindows();
return 0;
}
输出结果:
2. 图像分割
#include
#include
using namespace std;
using namespace cv;
using namespace cv::ml;
int main(int argc, char** argv)
{
Mat src = imread("E:/技能学习/opencv图像分割/test.jpg");
if (src.empty())
{
cout << "could not load image!" << endl;
return -1;
}
namedWindow("input image", WINDOW_AUTOSIZE);
imshow("input image", src);
//初始化
int numCluster = 3;
Scalar colorTab[] = {
Scalar(0,0,255),
Scalar(0,255,0),
Scalar(255,0,0),
Scalar(0,255,255), //红+绿 == 黄
};
int width = src.cols;
int height = src.rows;
int dims = src.channels();
int numsamples = width * height; //样本总数
Mat points(numsamples, dims, CV_64FC1); //样本矩阵 选择64位是为了精度更高
Mat labels; //存放表示每个簇的标签
Mat result = Mat::zeros(src.size(), CV_8UC3);
//图像RGB像素数据转换为样本数据
int index = 0;
for (int row = 0; row < height; row++)
{
for (int col = 0; col < width; col++)
{
index = row * width + col;
Vec3b rgb = src.at(row, col);
points.at(index, 0) = static_cast(rgb[0]);
points.at(index, 1) = static_cast(rgb[1]);
points.at(index, 2) = static_cast(rgb[2]);
}
}
int begin_time = getTickCount();
// EM Cluster Train
Ptr em_model = EM::create();
em_model->setClustersNumber(numCluster); //类别数
em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL); //协方差矩阵的类型
em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1)); //迭代停止的标准
em_model->trainEM(points, noArray(), labels, noArray()); //训练
//对每个像素标记颜色与显示
Mat sample(1, dims, CV_64FC1);
int end_time = getTickCount();
int r = 0, g = 0, b = 0;
for (int row = 0; row < height; row++)
{
for (int col = 0; col < width; col++)
{
index = row * width + col;
/*
//直接显示
int label = labels.at(index, 0);
Scalar c = colorTab[label];
result.at(row, col)[0] = c[0];
result.at(row, col)[1] = c[1];
result.at(row, col)[2] = c[2];
*/
//预言的方式显示
b = src.at(row, col)[0];
g = src.at(row, col)[1];
r = src.at(row, col)[2];
sample.at(0) = b;
sample.at(1) = g;
sample.at(2) = r;
int response = cvRound(em_model->predict2(sample, noArray())[1]);
Scalar c = colorTab[response];
result.at(row, col)[0] = c[0];
result.at(row, col)[1] = c[1];
result.at(row, col)[2] = c[2];
}
}
//cout << "execution time:" << (time - getTickCount()) / (getTickFrequency() * 1000) << endl;
cout << "execution time:" << ((end_time - begin_time)/ getTickFrequency()) << endl;
imshow("EM-Segmentation:",result);
waitKey(0);
destroyAllWindows();
return 0;
}
结果: