文章和代码已经归档至【Github仓库:https://github.com/timerring/dive-into-AI 】或者公众号【AIShareLab】回复 R语言 也可获取。
缺失值处理
在实际的数据分析中,缺失数据是常常遇到的。缺失值(missing values)通常是由于没有收集到数据或者没有录入数据。
例如,年龄的缺失可能是由于某人没有提供他(她)的年龄。大部分统计分析方法都假定处理的是完整的数据集。因此,除了一些专业化的书籍,大多数统计学教科书很少涉及这一问题。实际上,在进行正式的分析之前,我们需要在数据准备阶段检查数据集是否存在缺失值,并通过一些方法弥补因缺失值所造成的损失。
1. 识别缺失值
在 R 中,缺失值用 NA 表示,是“Not Available”的缩写。函数 is.na( ) 可以用于识别缺失值,其返回结果是逻辑值 TRUE 或 FALSE。
height <- c(100, 150, NA, 160)
height
# 100 150 160
is.na(height)
# FALSE FALSE TRUE FALSE 如果数据很少,缺失值的个数直接可以数出来,比如上面的变量 height 只有一个缺失值。但是如果数据量很大,就需要借助函数 table( ) 了。
table(is.na(height))
# FALSE TRUE
# 3 1 需要注意的是,任何包含 NA 的计算结果都是 NA。例如:
mean(height)
# 想要得到所有可参与计算的元素的平均值,应该先将 NA 从向量中移除。
mean(height, na.rm = TRUE)
# 136.666666666667参数 na.rm 表示移除缺失值,其意义与用函数 na.omit( ) 把缺失值省略是一样的。
mean(na.omit(height))注意,这里 na.omit( ) 是一个独立的函数,它能忽略输入对象中的缺失值,而 na.rm 只是计算描述性统计量的函数里的一个内部参数。
函数 summary( ) 在计算向量的统计量时会自动忽略缺失值,它会给出向量中缺失值的个数。例如:
summary(height)
# Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
# 100.0 125.0 150.0 136.7 155.0 160.0 1 2. 探索数据框里的缺失值
在决定如何处理缺失值之前,了解哪些变量有缺失值、数目有多少、是什么组合形式等是非常有意义的。下面用一个示例介绍探索缺失值模式的方法。
datasets 包里的数据集 iris 也称鸢尾花数据,它包含 150 个鸢尾花样品,分为 3 个品种(Species),每个品种各有 50 个样品。每个样品又包含 4 个属性,即花萼长度(Sepal.Length)、花萼宽度(Sepal.Width)、花瓣长度(Petal.Length)和花瓣宽度(Petal.Width)。该数据集不含缺失值。为了说明缺失值的处理方法,首先人为地生成一些缺失数据,以探索缺失值的模式和检验补全的效果。
missForest 包里的函数 prodNA( ) 可以随机生成缺失值,使用此函数前需要安装和加载 missForest 包。
options(warn=-1)
library(missForest)
data(iris)
# 为了使结果具有可重复性,我们用函数 `set.seed( )` 设置了生成随机数的种子。
set.seed(1234)
# 函数 prodNA( ) 默认生成数据数目 10% 的缺失值,我们可以通过改变参数 noNA 的值以生成不同数目的缺失值。
iris.miss <- prodNA(iris)
summary(iris.miss)从函数 summary( ) 的输出中可以看到每个变量里缺失值的数目。要了解数据集里缺失值的模式,用图形展示是一个好办法。VIM 包提供了大量可视化缺失值的函数,其中函数 aggr( ) 不仅展示每个变量里缺失值的个数(或比例),还展示多个变量组合下缺失值的个数(或比例)。例如:
library(VIM)
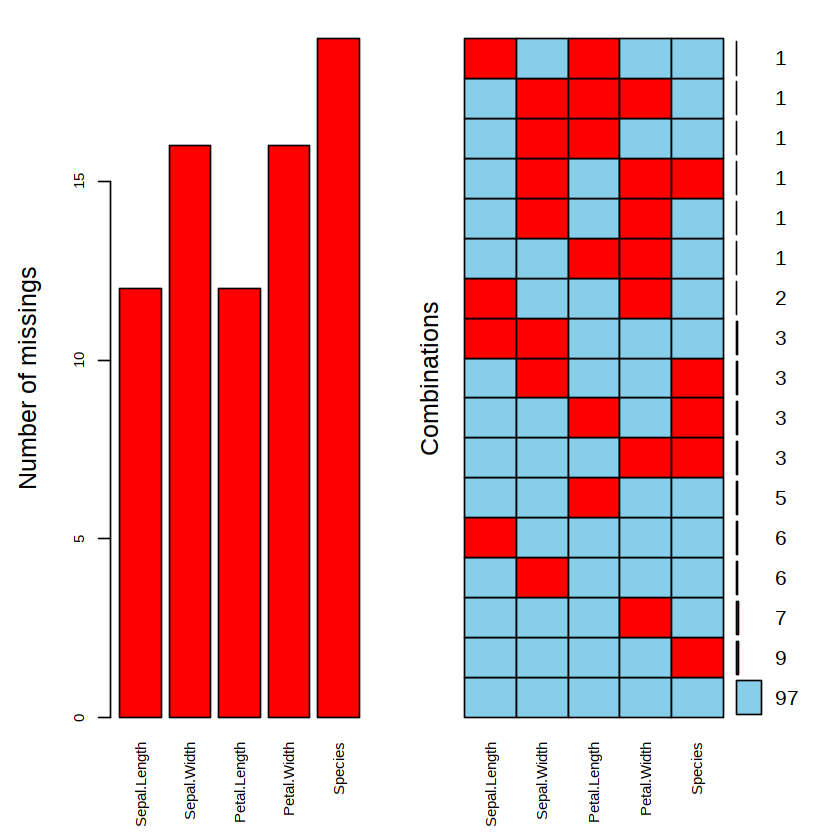
aggr(iris.miss, prop = FALSE, numbers = TRUE, cex.axis = 0.7)在上图中,第一幅图是用条形图展示了每个变量缺失值的个数,这与上面函数 summary( ) 的输出结果是一致的;第二幅图展示了数据框中 5 个变量不同组合下缺失值的个数,其中红色方块代表缺失值,最右边的数字代表个数。从最下面看起,共有 97 个鸢尾花样品没有缺失值,有 9 个鸢尾花样品知道它们的 4 个属性但不知道品种。
3. 填充缺失值
一般来说,处理缺失值可以采用下面 3 种方法:
- 删除,删除带有缺失值的变量或记录;
- 替换,用均值、中位数、众数或其他值替代缺失值;
- 补全,基于统计模型推测和补充缺失值。
上述方法都是在不得已时使用,无论哪种方法都不能完全弥补数据缺失带来的信息损失。因此,在数据收集阶段必须尽量避免数据的缺失。
3.1 删除缺失值:na.omit( )、complete.cases( )
如果缺失值的数量很小,删除后对分析结果影响不大,我们可以使用前面提到的函数 na.omit( ) 删除数据框中的缺失值。例如:
iris.sub <- na.omit(iris.miss)
nrow(iris.sub)删除缺失值后的数据框 iris.sub 只包含 97 条完整记录。此外,函数 complete.cases( ) 可以用来识别矩阵或数据框中没有缺失值的行,它的返回值是 TRUE 或 FALSE。如果某一行有完整的数据,返回 TRUE;如果某一行至少包含一个缺失值,则返回 FALSE。所以,上面的命令等价于:
iris.sub <- iris.miss[complete.cases(iris.miss), ]3.2 使用特定数值替换缺失值
如果不想直接删除缺失值,在某些情况下,还可以尝试使用特定的数值替换缺失值。
下面以变量 Sepal.Length 为例,用忽略缺失值后的均值替换该变量里的缺失值。先计算均值:
Sepal.Length.Mean <- mean(iris.miss$Sepal.Length, na.rm = TRUE)
Sepal.Length.Mean
# 5.78695652173913
# 用忽略缺失值后的均值替换该变量里的缺失值
iris.miss1 <- iris.miss
iris.miss1$Sepal.Length[is.na(iris.miss1$Sepal.Length)] <- Sepal.Length.Mean为检查补全后的数据与原始数据的差异,我们可以计算偏差:
summary((iris$Sepal.Length - iris.miss1$Sepal.Length)/iris$Sepal.Length)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# -0.258034 0.000000 0.000000 0.006871 0.000000 0.248447补全的平均偏差不到 1%,但最大偏差大约为 ±25%。
3.3 多重插补
多重插补(multiple imputation)是一种基于重复模拟的处理缺失值的方法,常用于处理比较复杂的缺失值问题。
R 中有多个可以实现缺失值多重插补的包,如 Amelia 包、mice 包和 mi 包等。其中 mice 包使用链式方程的多变量补全法,被广泛运用于数据清洗过程中。
mice 包假设数据是随机缺失的,并根据变量的类型建立模型得到预测值以代替缺失值。在这些模型里,常用的有:
- 预测均值匹配(pmm),实质上就是线性回归,适用于数值型变量;
- Logistic 回归(logreg),适用于二分类变量;
- 多分类 Logistic 回归(ployreg),适用于无序多分类变量;
- 比例优势比模型(polr),适用于有序多分类变量。
接下来,用函数 mice( ) 补全数据框 iris.miss 里的缺失值。
library(mice)
imputed.data <- mice(iris.miss, seed = 1234)
summary(imputed.data)
# PredictorMatrix:
# Sepal.Length Sepal.Width Petal.Length Petal.Width Species
# Sepal.Length 0 1 1 1 1
# Sepal.Width 1 0 1 1 1
# Petal.Length 1 1 0 1 1
# Petal.Width 1 1 1 0 1
# Species 1 1 1 1 0在上面输出结果的矩阵 PredictorMatrix 里,每一行代表含有缺失值的变量名,如果该行对应的某一列元素为 1,代表该列变量被用于建模预测。
从上面的输出结果中可以看出,对于每一个变量,其余变量都被用于它的缺失值预测。函数 mice( ) 的输出结果是一个列表,其中的对象 imp 也是一个列表,存放的是每个变量缺失值的插补值。例如,使用下面的命令可以得到变量 Sepal.Length 的插补值:
imputed.data$imp$Sepal.Length函数 mice( ) 通过 Gibbs 抽样完成,默认进行 5 次随机抽样,所以一共得到了 5 组插补值。我们可以通过查看上面的输出结果以检查插补值是否合理,然后选择其中的一组来补全。
例如,取 5 组插补值中的第 3 个:
complete.data <- complete(imputed.data, 3)为了检查缺失值的补全效果,对于数值型变量,我们可以计算插补值与原始变量值的偏差。
以变量 Sepal.Length 为例:
summary((iris$Sepal.Length-complete.data$Sepal.Length)/iris$Sepal.Length)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# -0.1428571 0.0000000 0.0000000 0.0007643 0.0000000 0.0945946补全的平均偏差不到 0.1%,最大偏差大约为 ±13%。因此,这里用多重插补法比用均值替换缺失值的方法效果更好。
数据框的最后一个变量 Species 是一个因子,包含 19 个缺失值。为了检查这种分类变量的缺失值的补全效果,我们可以用函数 table( ) 得到原始变量和插补后变量的列联表:
table(iris$Species, complete.data$Species)
# setosa versicolor virginica
# setosa 50 0 0
# versicolor 0 50 0
# virginica 0 1 49这种表被称为 混淆矩阵(confusion matrix),经常用于评价模型预测的准确度。对角线上的数字代表预测值和真实值一致的个数,非对角线上的数字代表预测值和真实值不一致的个数。
从上面的输出结果可以看出,变量 Species 的 19 个缺失值插补的正确率为 100%。