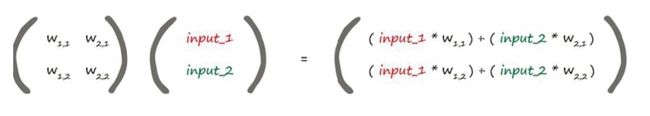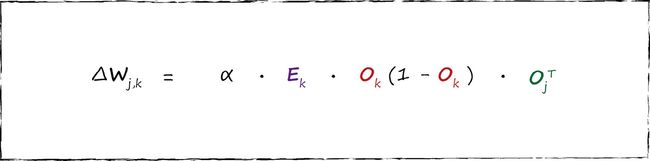1.神经网络基础知识
所有有用的计算机系统都有一个输入和一个输出, 并在输入和输出之间进行某种类型的计算。 神经网络也是如此。
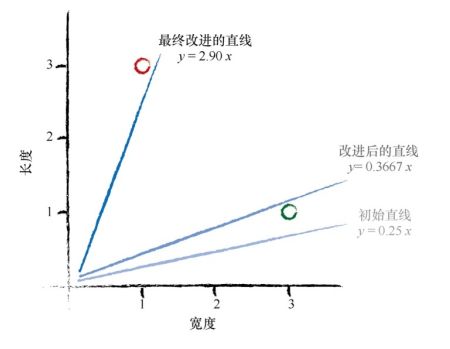
当我们不能精确知道一些事情如何运作时, 我们可以尝试使用模型来估计其运作方式, 在模型中, 包括了我们可以调整的参数。 如果我们不知道如何将千米转换为英里, 那么我们可以使用线性函数作为模型, 并使用可调节的梯度值作为参数。
改进这些模型的一种好方法是, 基于模型和已知真实示例之间的比较, 得到模型偏移的误差值, 调整参数——迭代。
我们使用简单的数学, 理解了线性分类器输出误差值和可调节斜率参数之间的关系。 也就是说, 我们知道了在何种程度上调整斜率, 可以消除输出误差值:
y = A x y=Ax y=Ax
E = ( Δ A ) x E=(\Delta A)x E=(ΔA)x
使用朴素的调整方法会出现一个问题, 即改进后的模型只与最后一次训练样本最匹配, “有效地”忽略了所有以前的训练样本。
解决这个问题的一种好方法是使用学习率, 调节改进速率, 这样单一的训练样本就不能主导整个学习过程。
Δ A = 学习率 L ( E / x ) \Delta A={\text{学习率}}L(E/x) ΔA=学习率L(E/x)
来自真实世界的训练样本可能充满噪声或包含错误。 适度更新有助于限制这些错误样本的影响。
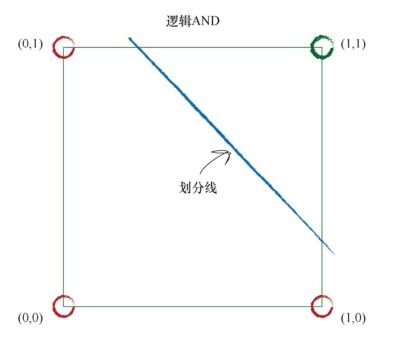
线性分类器可以学习部分布尔函数:
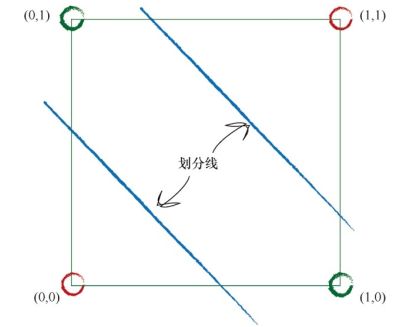
如果数据本身不是由单一线性过程支配, 那么一个简单的线性分类器不能对数据进行划分。 例如, 由逻辑XOR运算符支配的数据说明了这一点。
但是解决方案很容易, 你只需要使用多个线性分类器来划分由单一直线无法分离的数据。
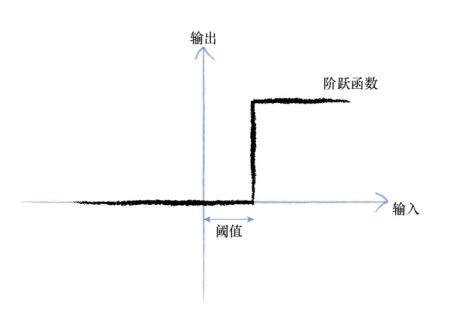
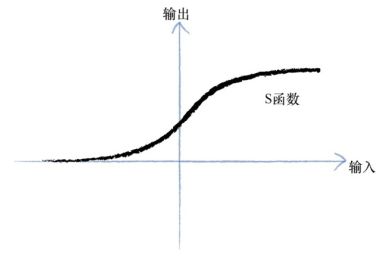
生物大脑的基本单元——即神经元——可以接收一个电输入,输出另一个电信号,但是我们不能将神经元表示为线性函数,因为神经元不会立即反应, 而是会抑制输入, 直到输入增强,强大到可以触发输出。 你可以这样认为, 在产生输出之前, 输入必须到达一个阈值。
我们可以使用更平滑的S形函数制作神经网络
S函数,有时也称为逻辑函数:
y = 1 1 + e − x y=\frac{1}{1+e^{-x}} y=1+e−x1
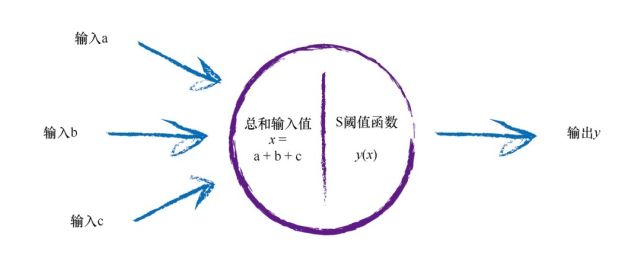
当然,生物神经元可以接受许多输入,在函数中,对于所有这些输入, 我们只需对它们进行相加,得到最终总和, 作为S函数的输入, 然后输出结果。 这实际上反映了神经元的工作机制。
每个神经元接受来自其之前多个神经元的输入,并且如果神经元被激发了, 它也同时提供信号给更多的神经元。
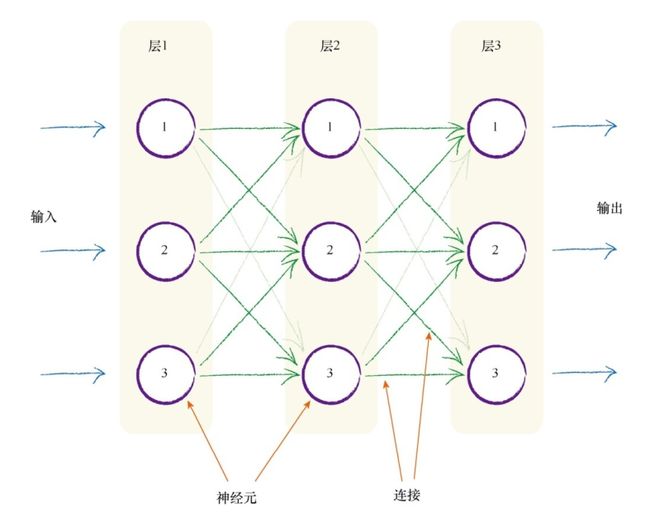
将这种自然形式复制到人造模型的一种方法是, 构建多层神经元, 每一层中的神经元都与在其前后层的神经元互相连接。
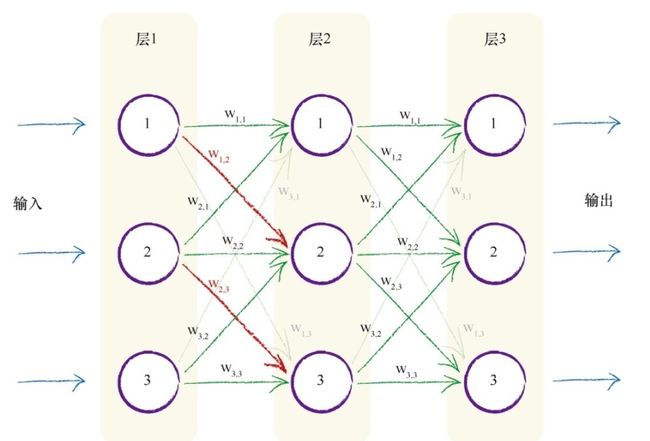
我们可以在多层神经元的连接上添加权重,从而弱化或放大信号,其权重值会随着神经网络的学习而按需变化,因此对于解决特定任务所需最小数量的连接冗余几个连接,也无伤大雅,因为它们的权重会逐渐接近零,即断开了链接。
为了简化神经网络的计算,我们使用矩阵
第一个矩阵包含两层节点之间的权重。 第二个矩阵包含第一层输入层的信号。 通过两个矩阵相乘, 我们得到的答案是输入到第二层节点组合调节后的信号。
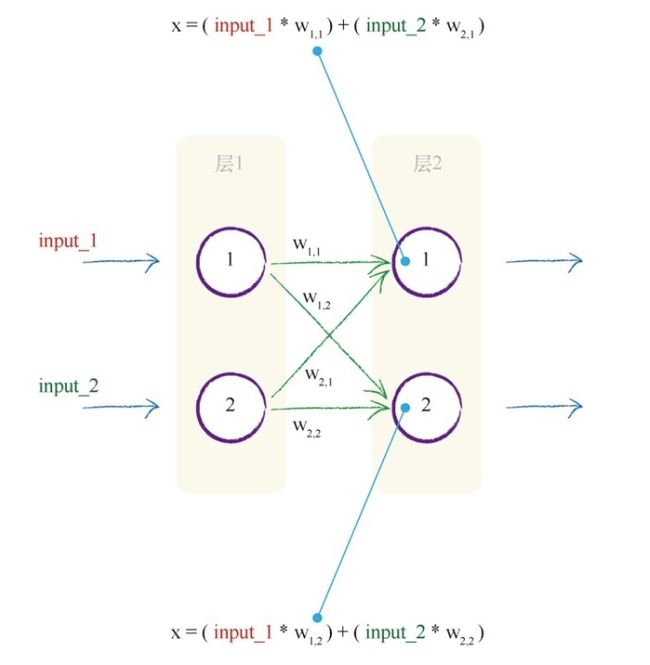
组合调节后的信号 X = 权重矩阵 W ⋅ 输入矩阵 I {\text{组合调节后的信号}}X={\text{权重矩阵}}W \cdot {\text{输入矩阵}}I 组合调节后的信号X=权重矩阵W⋅输入矩阵I
表达式X = W I适用于前后层之间的计算,之后对X矩阵的各值带入S函数计算即可
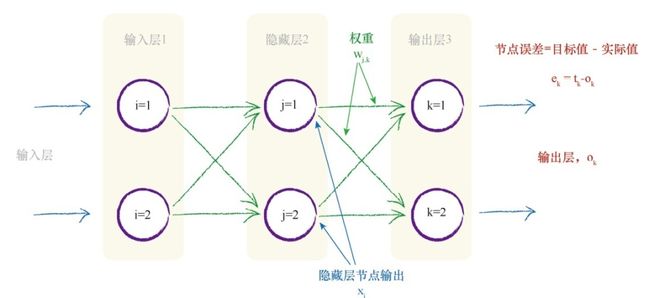
最左边的输入为输入层,最右边的输出为输出层,中间的多层为隐藏层
我们可以通过输出的误差来反向调节输入(反向传播),一种思想就是在所有造成误差的节点中平分误差,另一种思想是不等分误差。 与前一种思想相反, 我们为较大链接权重的连接分配更多的误差,因为这些链接对造成误差的贡献较大。
误差 e 1 ⋅ w 1 , 1 w 1 , 1 + w 2 , 2 {\text{误差}}e_1 \cdot {\frac {w_{1,1}}{w_{1,1}+w_{2,2}} } 误差e1⋅w1,1+w2,2w1,1
对于多层网络,我们从最终输出层往回工作,对于隐藏层的节点, 我们没有目标值或所希望的输出值。 我们只有最终输出层节点的目标值, 这个目标值来自于训练样本数据。隐藏层第一个节点具有两个链接, 这两个链接将这个节点连接到两个输出层节点。 我们知道, 沿着各个链接可以分割输出误差, 就像我们先前所做的一样。 这意味着, 对于中间层节点的每个链接, 我们得到了某种误差值。 我们可以重组这两个链接的误差, 形成这个节点的误差。 实际上我们没有中间层节点的目标值, 因此这种方法算得上第二最佳方法
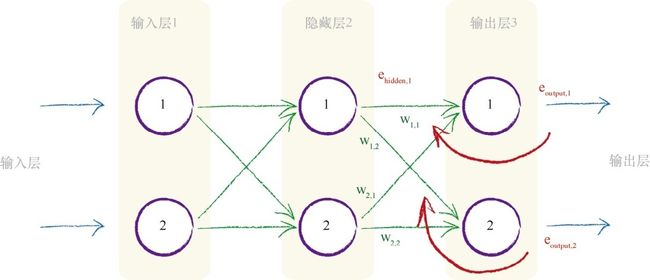
e h i d d e n , 1 = 链接 w 1 , 1 上的分割误差 + 链接 w 1 , 2 上的分割误差 = e o u t p u t , 1 ⋅ w 1 , 1 w 1 , 1 + w 2 , 2 + e o u t p u t , 2 ⋅ w 1 , 2 w 1 , 1 + w 2 , 2 \begin{aligned} e_{hidden,1} &= {\text{链接}}w_{1,1}上的分割误差 + {\text{链接}}w_{1,2}上的分割误差 \\ &=e_{output,1} \cdot {\frac {w_{1,1}}{w_{1,1}+w_{2,2}}} + e_{output,2} \cdot {\frac {w_{1,2}}{w_{1,1}+w_{2,2}}} \end{aligned} ehidden,1=链接w1,1上的分割误差+链接w1,2上的分割误差=eoutput,1⋅w1,1+w2,2w1,1+eoutput,2⋅w1,1+w2,2w1,2
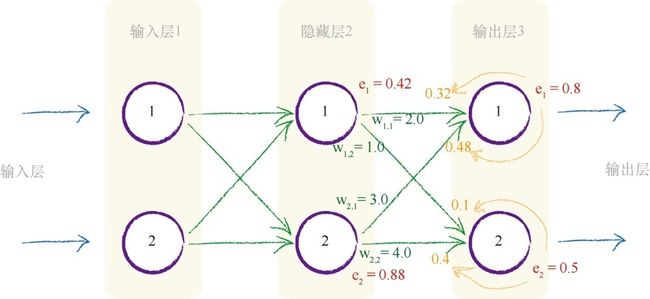
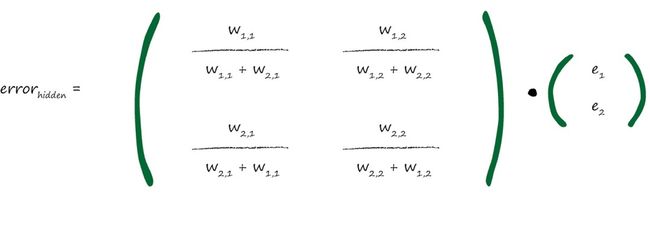
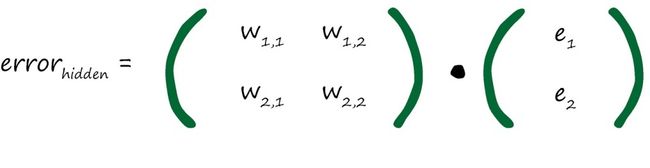
我们可以为隐藏层的误差构建矩阵,从而简化运算
分数的分母是一种归一化因子。 如果我们忽略了这个因子, 那么我们仅仅失去后馈误差的大小。
实践证明, 这种相对简单的误差信号反馈方式, 与我们先前相对复杂的方式一样有效。
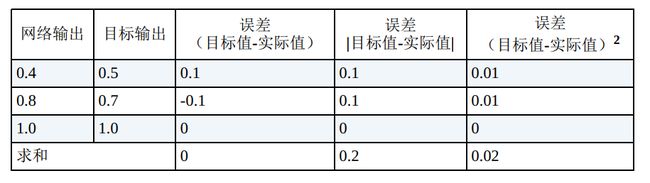
知道了误差,我们使用梯度下降——每走一步就观察地形,一步步下山——的方式更新权重,同时,要更好地到达目标,我们要动态地变化“步幅”,这就需要使用合适的误差函数:
我们更喜欢使用第三种误差函数, 而不喜欢使用第二种误差函数, 原因有以下几点:
- 使用误差的平方, 我们可以很容易使用代数计算出梯度下降的斜率。
- 误差函数平滑连续, 这使得梯度下降法很好地发挥作用——没有间断, 也没有突然的跳跃。
- 越接近最小值, 梯度越小, 这意味着, 如果我们使用这个函数调节步长, 超调的风险就会变得较小。
要使用梯度下降的方法, 现在我们需要计算出误差函数相对于权重的斜率。此处,我们感兴趣的是, 误差函数是如何依赖于神经网络中的链接权重的。 换句话说:“误差对链接权重的改变有多敏感? ”
∂ E ∂ w j , k \frac{\partial E}{\partial w_{j,k}} ∂wj,k∂E
这个表达式表示了当权重 wj,k 改变时, 误差E是如何改变的。 这是误差函数的斜率, 也就是我们希望使用梯度下降的方法到达最小值的方向。
首先展开误差函数, 这是对目标值和实际值之差的平方进行求和, 这是针对所有n个输出节点的和。
∂ E ∂ w j , k = ∂ ∑ n ( t n − o n ) 2 ∂ w j , k \frac{\partial E}{\partial w_{j,k}}={\frac{\partial \sum_n(t_n-o_n)^2}{\partial w_{j,k}}} ∂wj,k∂E=∂wj,k∂∑n(tn−on)2
节点n的输出 on 只取决于连接到这个节点的链接, 因此我们可以直接简化这个表达式。这意味着, 由于 wj,k 是链接到节点k的权重, 因此节点k的输出 ok 只取决于权重 wj,k ,除了权重 wj,k 所链接的节点(也就是 ok )外,我们可以从和中删除所有的 on , 这就完全删除了令人厌烦的求和运算。
∂ E ∂ w j , k = ∂ ( t k − o k ) 2 ∂ w j , k \frac{\partial E}{\partial w_{j,k}}={\frac{\partial(t_k-o_k)^2}{\partial w_{j,k}}} ∂wj,k∂E=∂wj,k∂(tk−ok)2
使用链式法则可得
∂ E ∂ w j , k = ∂ ( t k − o k ) 2 ∂ o k ⋅ ∂ o k ∂ w j , k = − 2 ( t k − o k ) ⋅ ∂ o k ∂ w j , k \begin{aligned} \frac{\partial E}{\partial w_{j,k}}&={\frac{\partial(t_k-o_k)^2}{\partial o_k}} \cdot {\frac{\partial o_k}{\partial w_{j,k}}}\\ &=-2(t_k - o_k)\cdot {\frac{\partial o_k}{\partial w_{j,k}}} \end{aligned} ∂wj,k∂E=∂ok∂(tk−ok)2⋅∂wj,k∂ok=−2(tk−ok)⋅∂wj,k∂ok
ok 是节点k的输出,是在连接输入信号上进行加权求和, 在所得到结果上应用S函数得到的结果。
∂ E ∂ w j , k = − 2 ( t k − o k ) ⋅ ∂ s i g m o i d ( ∑ j w j , k ⋅ o j ) ∂ w j , k \frac{\partial E}{\partial w_{j,k}}=-2(t_k - o_k) \cdot {\frac{\partial {sigmoid(\sum_jw_{j,k}\cdot o_j)}}{\partial w_{j,k}}} ∂wj,k∂E=−2(tk−ok)⋅∂wj,k∂sigmoid(∑jwj,k⋅oj)
oj 是前一个隐藏层节点的输出, 而不是最终层的输出 ok 。
S函数的微分公式:
∂ s i g m o i d ( x ) ∂ x = s i g m o i d ( x ) ⋅ ( 1 − s i g m o i d ( x ) ) \frac{\partial sigmoid(x)}{\partial x}=sigmoid(x) \cdot (1-sigmoid(x)) ∂x∂sigmoid(x)=sigmoid(x)⋅(1−sigmoid(x))
带入可得:
∂ E ∂ w j , k = − 2 ( t k − o k ) ⋅ ∂ s i g m o i d ( ∑ j w j , k ⋅ o j ) ∂ ∑ j w j , k ⋅ o j ⋅ ∂ ∑ j w j , k ⋅ o j ∂ w j , k = − 2 ( t k − o k ) ⋅ s i g m o i d ( ∑ j w j , k ⋅ o j ) ⋅ ( 1 − s i g m o i d ( ∑ j w j , k ⋅ o j ) ) ⋅ ∂ ∑ j w j , k ⋅ o j ∂ w j , k = − 2 ( t k − o k ) ⋅ s i g m o i d ( ∑ j w j , k ⋅ o j ) ⋅ ( 1 − s i g m o i d ( ∑ j w j , k ⋅ o j ) ) ⋅ o j \begin{aligned} \frac{\partial E}{\partial w_{j,k}}&=-2(t_k - o_k) \cdot {\frac{\partial {sigmoid(\sum_jw_{j,k}\cdot o_j)}}{\partial \sum_jw_{j,k}\cdot o_j}}\cdot {\frac{\partial \sum_jw_{j,k}\cdot o_j}{\partial w_{j,k}}}\\ &=-2(t_k - o_k) \cdot sigmoid(\sum_jw_{j,k}\cdot o_j)\cdot (1-sigmoid(\sum_jw_{j,k}\cdot o_j))\cdot {\frac{\partial \sum_jw_{j,k}\cdot o_j}{\partial w_{j,k}}}\\ &=-2(t_k - o_k) \cdot sigmoid(\sum_jw_{j,k}\cdot o_j)\cdot (1-sigmoid(\sum_jw_{j,k}\cdot o_j))\cdot o_j \end{aligned} ∂wj,k∂E=−2(tk−ok)⋅∂∑jwj,k⋅oj∂sigmoid(∑jwj,k⋅oj)⋅∂wj,k∂∑jwj,k⋅oj=−2(tk−ok)⋅sigmoid(j∑wj,k⋅oj)⋅(1−sigmoid(j∑wj,k⋅oj))⋅∂wj,k∂∑jwj,k⋅oj=−2(tk−ok)⋅sigmoid(j∑wj,k⋅oj)⋅(1−sigmoid(j∑wj,k⋅oj))⋅oj
去掉倍数2。我们只对误差函数的斜率方向感兴趣, 这样我们就可以使用梯度下降的方法, 因此可以去掉2。
∂ E ∂ w j , k = − ( t k − o k ) ⋅ s i g m o i d ( ∑ j w j , k ⋅ o j ) ( 1 − s i g m o i d ( ∑ j w j , k ⋅ o j ) ) ⋅ o j \frac{\partial E}{\partial w_{j,k}}=-(t_k - o_k) \cdot sigmoid(\sum_jw_{j,k}\cdot o_j)(1-sigmoid(\sum_jw_{j,k}\cdot o_j))\cdot o_j ∂wj,k∂E=−(tk−ok)⋅sigmoid(j∑wj,k⋅oj)(1−sigmoid(j∑wj,k⋅oj))⋅oj
第一部分, 非常简单, 就是(目标值-实际值),我们对此已经很清楚了。 第二部分,在sigmoid中的求和表达式也很简单, 就是进入最后一层节点的信号,我们可以称之为 ik , 这样它看起来比较简单。 这是应用激活函数之前, 进入节点的信号。 最后一部分是前一隐藏层节点j的输出。
我们所得到的这个表达式, 是为了优化隐藏层和输出层之间的权重。 现在, 我们需要完成工作, 为输入层和隐藏层之间的权重找到类似的误差斜率
∂ E ∂ w i , j = − ( e j ) ⋅ s i g m o i d ( ∑ i w i , j ⋅ o i ) ( 1 − s i g m o i d ( ∑ i w i , j ⋅ o i ) ) ⋅ o i \frac{\partial E}{\partial w_{i,j}}=-(e_j) \cdot sigmoid(\sum_iw_{i,j}\cdot o_i)(1-sigmoid(\sum_iw_{i,j}\cdot o_i))\cdot o_i ∂wi,j∂E=−(ej)⋅sigmoid(i∑wi,j⋅oi)(1−sigmoid(i∑wi,j⋅oi))⋅oi
第一部分的(目标值-实际值)误差,现在变成了隐藏层节点中重组的向后传播误差,正如在前面所看到的那样, 我们称之为 ej 。sigmoid部分可以保持不变, 但是内部的求和表达式指的是前一层, 因此求和的范围是所有由权重调节的进入隐藏层节点j的输入。 我们可以称之为 ij 。现在,最后一部分是第一层节点的输出 oi , 这碰巧是输入信号。
我们使用学习因子调节变化, 我们可以根据特定的问题, 调整这个学习因子。 当我们建立线性分类器,它作为避免被错误的训练样本拉得太远的一种方式, 同时也为了保证权重不会由于持续的超调而在最小值附近来回摆动。
new w j , k = old w j , k − α ⋅ ∂ E ∂ w j , k {\text{new}w_{j,k}}={\text{old}}w_{j,k}-\alpha \cdot {\frac{\partial E}{\partial w_{j,k}}} newwj,k=oldwj,k−α⋅∂wj,k∂E
更新后的权重 wj,k 是由刚刚得到误差斜率取反来调整旧的权重而得到的。正如我们先前所看到的,如果斜率为正,我们希望减小权重,如果斜率为负,我们希望增加权重,因此,我们要对斜率取反。
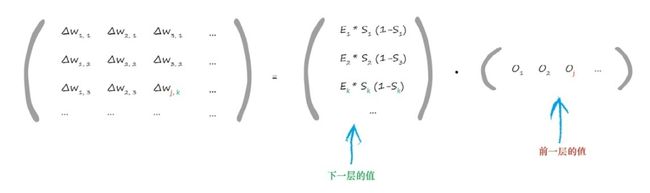
通过矩阵计算:
权重改变矩阵中包含的值, 这些值可以调整链接权重 wj,k ,这个权重链接了当前层节点j与下一层节点k。你可以发现,表达式中的第一项使用下一层(节点k)的值,最后一项使用前一层(节点j)的值
权重更新矩阵有如下的矩阵形式, 这种形式可以让我们通过计算机编程语言高效地实现矩阵运算。
S激活函数,如果输入变大,函数会变得平坦,由于我们使用梯度学习新的权重, 因此一个平坦的激活函数会出问题。
权重的改变取决于激活函数的梯度,小梯度意味着限制神经网络学习的能力,这就是所谓的饱和神经网络。 这意味着,我们应该尽量保持小的输入。同时还取决于输入信号 oj ,因此,我们也不应
该让输入信号太小。当计算机处理非常小或非常大的数字时,可能会丧失精度,因此,使用非常小的值也会出现问题。
重新调整输入值,将其范围控制在0.0到1.0。输入0会将 oj 设置为0,这样权重更新表达式就会等于0,从而造成学习能力的丧失, 因此在某些情况下, 我们会将此输入加上一个小小的偏移, 如0.01,避免输入0带来麻烦。
S激活函数的输出不可能大于1.0、小于0。如果我们将目标值设置在这些不可能达到的范围, 训练网络将会驱使更大的权重, 以获得越来越大的输出, 而这些输出实际上是不可能由激活函数生成的。 这使得网络饱和, 因此我们知道这种情况是很糟糕的。
因此, 我们应该重新调整目标值, 匹配激活函数的可能输出, 注意避开激活函数不可能达到的值。虽然, 常见的使用范围为0.0~1.0, 但是由于0.0和1.0这两个数也不可能是目标值, 并且有驱动产生过大的权重的风险, 因此一些人也使用0.01~0.99的范围。
内部链接的权重应该是随机的, 值较小, 但要避免零值。 如果节点的传入链接较多, 有一些人会使用相对复杂的规则, 如减小这些权重的大小。