2.神经网络的实现

创建神经网络类

import numpy
# scipy.special包含S函数expit(x)
import scipy.special
# 打包模块
import pickle

# 激活函数
def activation_func(x):
    return scipy.special.expit(x)

# 用于创建、 训练和查询3层神经网络
class neuralNetwork:
    # 初始化神经网络
    def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
        # 设置 输入层, 隐藏层, 输出层 结点个数
        self.inodes = inputnodes
        self.hnodes = hiddennodes
        self.onodes = outputnodes
        # 两个链接权重矩阵 wih, who
        # w11 w21
        # w12 w22 etc
        self.wih = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))
        self.who = numpy.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))
        # 学习率
        self.lr = learningrate
        # 激活函数是S函数，使用lambda定义函数
        # self.activation_function = lambda x: scipy.special.expit(x)
        # 使用lambda定义函数时无法打包保存神经网络对象

        self.activation_function = activation_func
        pass

    # 训练神经网络
    def train(self, inputs_list, targets_list):
        # 使用完全相同的方式从输入层前馈信号到最终输出层,因此代码几乎与query()相同
        inputs = numpy.array(inputs_list, ndmin=2).T
        # 使用包含期望值训练样本来训练网络
        targets = numpy.array(targets_list, ndmin=2).T
        hidden_inputs = numpy.dot(self.wih, inputs)
        hidden_outputs = self.activation_function(hidden_inputs)
        final_inputs = numpy.dot(self.who, hidden_outputs)
        # 此处的final_outputs和上面的hidden_outputs都经过了激活函数,后面更新权重时不需要再代入了
        final_outputs = self.activation_function(final_inputs)

        # 期望矩阵和输出矩阵相减获得误差矩阵
        output_errors = targets - final_outputs
        # 根据所连接的权重分割误差，为每个隐藏层结点重组这些误差
        hidden_errors = numpy.dot(self.who.T, output_errors)
        # 应用更新权重的矩阵形式表达式
        # 学习率*误差Ek*sigmoid(输出Ok)*(1-sigmoid(Ok))·前一层输出OjT
        self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs))
        self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs))
        pass

    # 查询神经网络,接受输入,返回输出
    def query(self, inputs_list):
        # 将输入列表转换成二维列表,保证计算类型正确
        inputs = numpy.array(inputs_list, ndmin=2).T
        # 输入层-隐藏层权重矩阵 点乘 输入矩阵 = 隐藏层输入
        hidden_inputs = numpy.dot(self.wih, inputs)
        # 隐藏层输入应用激活函数
        hidden_outputs = self.activation_function(hidden_inputs)
        # 隐藏层-输出层权重矩阵 点乘 输隐藏层输出矩阵 = 输出层输入
        final_inputs = numpy.dot(self.who, hidden_outputs)
        # 输出层输入应用激活函数
        final_outputs = self.activation_function(final_inputs)
        return final_outputs

---

数据集采用在人工智能领域流行的手写数字的MNIST数据库，MNIST数据库的格式不容易使用， 因此其他人已经创建了相对简单的数据文件格式——CSV文件，其纯文本中的每一个值都是由逗号分
隔的。

训练集是用来训练神经网络的60 000个标记样本集。标记是指输入与期望的输出匹配，也就是答案应该是多少。
可以使用较小的只有10 000个样本的测试集来测试我们的想法或算法工作的好坏程度。 由于这也包含了正确的标记， 因此可以观察神经网络是否得到正确的答案。

在文本中， 这些记录或这些行的内容很容易理解：
第一个值是标签， 即书写者实际希望表示的数字， 如“7”或“9”。 这是我们希望神经网络学习得到的正确答案。随后的值，由逗号分隔，是手写体数字的像素值。像素数组的尺寸是28乘以28，因此在标签后有784个值。

# 读取并显示数据集数据表示的含义
import numpy
import matplotlib.pyplot as plt
# %matplotlib inline


data_file = open(".../mnist_train_100.csv", 'r')
data_list = data_file.readlines()
data_file.close()
print(len(data_list))

# 显示第一个
all_values = data_list[0].split(',')
# 将文本字符串转换成实数, .reshape((28,28))可以确保数字列表每28个元素折返一次,形成28乘28的方形矩阵
image_array = numpy.asfarray(all_values[1:]).reshape((28, 28))
# 对图像做处理
plt.imshow(image_array, cmap='Greys', interpolation='None')
# 显示图像
plt.show()

---

在将数据抛给神经网络之前需要准备数据

我们先前看到，如果输入数据和输出值， 形状正好适合， 这样它们就可以待在网络节点激活函数的舒适区域内，那么神经网络的工作会更出色。

我们需要做的第一件事情是将输入颜色值从较大的0到255的范围，缩放至较小的0.01 到 1.0的范围。 我们刻意选择0.01作为范围最低点，是为了避免先前观察到的0值输入最终会人为地造成权重更新失败。我们没有选择0.99作为输入的上限值， 是因为不需要避免输入1.0会造成这个问题。 我们只需要避免输出值为1.0。

将在0到255范围内的原始输入值除以255，就可以得到0到1范围的输入值。

然后，需要将所得到的输入乘以0.99，把它们的范围变成0.0 到0.99。接下来，加上0.01，将这些值整体偏移到所需的范围0.01到1.00。

scaled_input = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01

现在， 我们需要思考神经网络的输出。 先前， 我们看到输出值应该匹配激活函数可以输出值的范围。 我们使用的逻辑函数不能输出如 -2.0 或 255 这样的数字，能输出的范围为0.0到1.0，事实上不能达到0.0或1.0，这是逻辑函数的极限值，逻辑函数仅接近这两个极限，但不能真正到达那里。因此，看起来在训练时必须调整目标值。

我们要求神经网络对图像进行分类， 分配正确的标签。 这些标签是0到9共10个数字中的一个。 这意味着神经网络应该有10个输出层节点， 每个节点对应一个可能的答案或标签。 如果答案是“0”， 输出层第一个节点激发， 而其余的输出节点则保持抑制状态。

依照这种方向，我们可以构建目标矩阵

onodes = 10
targets = numpy.zeros(onodes) + 0.01
targets[int(all_values[0])] = 0.99

---

# 训练网络
def train_network(network, output_nodes, train_path, epochs):

    # 加载MNIST训练数据集
    training_data_file = open(train_path, 'r')
    training_data_list = training_data_file.readlines()
    training_data_file.close()
    # 训练世代,即训练几次
    for e in range(epochs):
        # 遍历读取的训练集
        for record in training_data_list:
            all_values = record.split(',')
            # 将文本字符串转换成实数,并将输入颜色值从0~255缩小为0.01~1.0，保证输入
            inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
            # 目标数组
            targets = numpy.zeros(output_nodes) + 0.01
            # 设置目标数字对应的数组内容为0.99
            targets[int(all_values[0])] = 0.99
            network.train(inputs, targets)
            pass
        pass

# 测试单个输入
def query_network_one_input(network, img_data):
    # 设置输入
    inputs = (numpy.asfarray(img_data[:]) / 255.0 * 0.99) + 0.01
    # 查询网络
    outputs = network.query(inputs)
    # 取出输出数组中的最高值对应的下标
    label = numpy.argmax(outputs)
    return label


# 测试文件，文件中有多条数据
def query_network(network, test_path):
    # 读取测试数据
    test_data_file = open(test_path, 'r')
    test_data_list = test_data_file.readlines()
    test_data_file.close()

    # 评分表,回答正确添加一个1
    scorecard = []

    for record in test_data_list:
        all_values = record.split(',')
        # 取出目标数字
        correct_label = int(all_values[0])
        print("aim=", correct_label, end="")
        # 设置输入
        inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
        # 查询网络
        outputs = network.query(inputs)
        # 取出输出数组中的最高值对应的下标
        label = numpy.argmax(outputs)
        print("ans=", label)
        # 设置评分表
        if (label == correct_label):
            scorecard.append(1)
        else:
            scorecard.append(0)
            pass
        pass

    # 计算正确率
    scorecard_array = numpy.asarray(scorecard)
    print("performance = ", scorecard_array.sum() / scorecard_array.size)


# 保存神经网络对象
def save_network(path, network):
    with open(path, 'wb') as f:
        pickle.dump(network, f)


# 加载神经网络对象
def load_network(path):
    with open(path, 'rb') as f:
        network = pickle.load(f)
    return network

---

改进网络

调整学习率

学习率是影响梯度下降发生速度的重要参数。

多次运行

通过提供更多爬下斜坡的机会， 有助于在梯度下降过程中进行权重更新

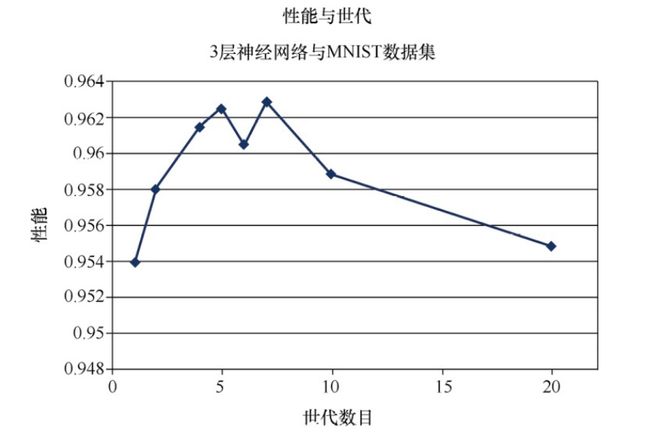
结果呈现出不可预测性。 在大约5或7个世代时， 有一个甜蜜点。 在此之后， 性能会下降， 这可能是过度拟合的效果。 性能在6个世代的情况下下降， 这可能是运行中出了问题， 导致网络在梯度下降过程中被卡在了一个局部的最小值中。 事实上， 由于没有对每个数据点进行多次实验， 无法减
小随机过程的影响，

直观上， 如果你打算使用更长的时间（多个世代） 探索梯度下降， 那么你可以承受采用较短的步长（学习率） ， 并且在总体上可以找到更好的路径， 这是有道理的。 确实， 对于MNIST学习任务， 我们的神经网络的甜蜜点看起来是5个世代。 请再次记住， 我们在使用一种相当不科学的方式来进行实验。 要正确、 科学地做到这一点， 就必须为每个学习率和世代组合进行多次实验， 尽量减少在梯度下降过程中随机性的影响。

---

改变网络形状

随着增加隐藏层节点的数量， 结果有所改善， 但是不显著。 由于增加一个隐藏层节点意味着增加了到前后层的每个节点的新网络链接， 这一切都会产生额外较多的计算， 因此训练网络所用的时间也显著增加了！ 因此， 必须在可容忍的运行时间内选择某个数目的隐藏层节点。

---

手写数字

import imageio.v2 as imageio
import neuralNetwork
import splitimg

# 分割图片保存目录
test = ".../test/"

# 分析含有多个数字的图片
def parse_img_numbers(img_path, network):
    result = 0
    number = splitimg.split_img(img_path, test)
    for i in range(0, number):
        img_array = imageio.imread(test + '%d.jpg' % i, pilmode='L')
        img_data = 255.0 - img_array.reshape(784)
        label = neuralNetwork.query_network_one_input(network, img_data)
        result += label * pow(10, number-1)
        number -= 1
    print(result)

# 分析只有一个数字的图片
def parse_img(img_path, network):
    img_array = imageio.imread(img_path, pilmode='L')
    img_data = 255.0 - img_array.reshape(784)
    label = neuralNetwork.query_network_one_input(network, img_data)
    return label

# 按数字分割图片
import cv2
import numpy as np

P_A = 10


def split_img(source_path, temp_save_path):

    # 图像resize
    dsize = 28
    img = cv2.imread(source_path)
    data = np.array(img)
    height = data.shape[0]
    width = data.shape[1]
    # 设置最小的文字像素高度
    min_val = 10

    start_i = -1
    end_i = -1
    # 存放每行的起止坐标
    rowinfo = []

    # 行分割
    for i in range(height):

        # 行中有字相关信息
        if (not data[i].all()):
            end_i = i
            if (start_i < 0):
                start_i = i
                pass
        # 行中无字相关信息
        elif (data[i].all() and start_i >= 0):
            if (end_i - start_i >= min_val):
                rowinfo.append((start_i, end_i))
                pass
            start_i, end_i = -1, -1

    # 列分割
    start_j = -1
    end_j = -1
    # 最小文字像素宽度
    min_val_word = 5
    # 分割后保存编号
    number = 0
    for start, end in rowinfo:
        for j in range(width):
            # 列中有字相关信息
            if (not data[start: end, j].all()):
                end_j = j
                if (start_j < 0):
                    start_j = j
                    pass
            # 列中无字信息
            elif (data[start: end, j].all() and start_j >= 0):
                if (end_j - start_j >= min_val_word):
                    img = data[start:end, start_j: end_j]
                    im2save = cv2.resize(cv2.copyMakeBorder(
                        img, P_A, P_A, P_A, P_A, cv2.BORDER_CONSTANT, value=(255, 255, 255)), (28, 28))  # 归一化处理
                    cv2.imwrite(temp_save_path + '%d.jpg' % number, im2save)
                    number += 1
                    pass
                start_j, end_j = -1, -1

    return number

---

让我们来看看是否可以到神经网络内部一探究竟， 是否能够理解神经网络所学习到的知识， 将神经网络通过训练搜集到的知识可视化。

我们可以观察权重， 这毕竟是神经网络学习的内容。 但是， 权重不太可能告诉我们太多信息。 特别是， 神经网络的工作方式是将学习分布到不同的链接权重中。 这种方式使得神经网络对损坏具有了弹性， 这就像是生物大脑的运行方式。 删除一个节点甚至相当多的节点， 都不太可能彻底破坏神经网络良好的工作能力。

向后查询

https://github.com/makeyourownneuralnetwork/makeyourownneuralnetwork/blob/master/part3_neural_network_mnist_backquery.ipynb

上面是反向查询神经网络的代码

---

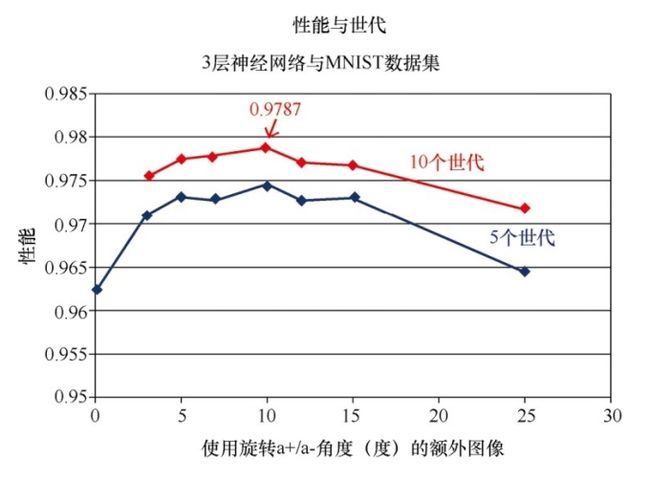
为了学习多样的变化类型，我们可以通过旋转图像创建新的训练数据

# create rotated variations
# rotated anticlockwise by 10 degrees
inputs_plus10_img = scipy.ndimage.interpolation.rotate(scaled_input.reshape(28,28), 10,cval=0.01, reshape=False)
# rotated clockwise by 10 degrees
inputs_minus10_img=scipy.ndimage.interpolation.rotate(scaled_input.reshape(28,28), -10,cval=0.01, reshape=False)