cs231n assignment2 q1
文章目录
- 嫌啰嗦看源码
- Q1 Multi-Layer Fully Connected Neural Networks 多层全连接神经网络
-
- fc_net
-
- \_\_init\_\_
-
- 题面
- 解析
- 代码
- loss
-
- 题面
- 解析
- 代码
- 输出
- 调整一个三层神经网络使其过拟合
-
- 题面
- 解析
- 结果
- 调整一个五层神经网络使其过拟合
-
- 结果
- Inline Question 1
-
- 题面
- 答案
- update_rules
- sgd_momentum
-
- 题面
- 解析
- 代码
- 输出
- RMSProp
-
- 题面
- 解析
- 代码
- 输出
- Adam
-
- 题面
- 解析
- 代码
- 输出
- train you best model
-
- 题面
- 解析
- 代码
- 输出
嫌啰嗦看源码
Q1 Multi-Layer Fully Connected Neural Networks 多层全连接神经网络

在layers.py中我们可以直接用assignment1 里面的已经写好的affine_forward ,affine_backward,relu_forward,relu_backward的几个方法,不用重新再写了
fc_net
这里的fc_net跟之前assignment1 q4的神经网络不同,之前的神经网络层数是固定的两层,这一次的神经网络是任意多层,因此我们需要使用循环来实现层数的定义,总之具体的细节看代码就能理解
__init__
题面
初始化网络的参数,将所有值存储在self.params字典中。
将第一层的权重和偏差存储在W1和b1中;对于第二层,使用W2和b2等。
权重应从以0为中心的正态分布初始化,标准偏差等于weight_scale。
偏差应初始化为零。
当使用批量归一化时,将第一层的缩放和偏移参数存储在gamma1和beta1中;
对于第二层,使用gamma2和beta2等。缩放参数应初始化为1,移位参数应初始化至0。
可以看到init函数跟之前的有了很大的不同
翻译一下其中初始化的时候传进来的参数的释义
- hidden_dims :一个整数类型列表,代表中隐藏层各层的维度
- input_dim: 一个整数代表输入数据的维度
- num_classes:一个整数代表着需要去分类的数量,也就是最后一层输出层的维度
- dropout_keep_ratio:丢弃强度,0和1之间的标量,如果drop_keep_ratio = 1 则网络不会丢弃层
- normalization:网络会使用哪种正则类型,可用的选择有"batchnorm","layernorm"或者None代表着不适用正则(默认)
- reg:给出L2正则化强度的标量
- weight_scale: 标量,给出权重随机初始化的标准偏差。
- dtype:数据类型
- seed:如果不是None,那么将这个随机种子传递给丢弃层。这将使丢弃层具有决定性,这样我们就可以对模型进行梯度检查。
解析
注意最后一层不需要正则项的参数
代码
def __init__(
self,
hidden_dims,
input_dim=3 * 32 * 32,
num_classes=10,
dropout_keep_ratio=1,
normalization=None,
reg=0.0,
weight_scale=1e-2,
dtype=np.float32,
seed=None,
):
"""Initialize a new FullyConnectedNet.
Inputs:
- hidden_dims: A list of integers giving the size of each hidden layer.
- input_dim: An integer giving the size of the input.
- num_classes: An integer giving the number of classes to classify.
- dropout_keep_ratio: Scalar between 0 and 1 giving dropout strength.
If dropout_keep_ratio=1 then the network should not use dropout at all.
- normalization: What type of normalization the network should use. Valid values
are "batchnorm", "layernorm", or None for no normalization (the default).
- reg: Scalar giving L2 regularization strength.
- weight_scale: Scalar giving the standard deviation for random
initialization of the weights.
- dtype: A numpy datatype object; all computations will be performed using
this datatype. float32 is faster but less accurate, so you should use
float64 for numeric gradient checking.
- seed: If not None, then pass this random seed to the dropout layers.
This will make the dropout layers deteriminstic so we can gradient check the model.
"""
self.normalization = normalization
self.use_dropout = dropout_keep_ratio != 1
self.reg = reg
self.num_layers = 1 + len(hidden_dims)
self.dtype = dtype
self.params = {}
############################################################################
# TODO: Initialize the parameters of the network, storing all values in #
# the self.params dictionary. Store weights and biases for the first layer #
# in W1 and b1; for the second layer use W2 and b2, etc. Weights should be #
# initialized from a normal distribution centered at 0 with standard #
# deviation equal to weight_scale. Biases should be initialized to zero. #
# #
# When using batch normalization, store scale and shift parameters for the #
# first layer in gamma1 and beta1; for the second layer use gamma2 and #
# beta2, etc. Scale parameters should be initialized to ones and shift #
# parameters should be initialized to zeros. #
############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# 获取所有层数的维度
layer_dims = [input_dim] + hidden_dims + [num_classes]
# 初始化所有层的参数 (这里的层数是上面的layer_dims的长度减1,因此不会下标越界)
for i in range(self.num_layers):
self.params['W' + str(i + 1)] = np.random.normal(0, weight_scale, size=(layer_dims[i], layer_dims[i + 1]))
self.params['b' + str(i + 1)] = np.zeros(layer_dims[i + 1])
# 接下来添加batch normalization 层,注意最后一层不需要添加
if self.normalization == 'batchnorm' and i < self.num_layers - 1:
self.params['gamma' + str(i + 1)] = np.ones(layer_dims[i + 1])
self.params['beta' + str(i + 1)] = np.zeros(layer_dims[i + 1])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
############################################################################
# END OF YOUR CODE #
############################################################################
# When using dropout we need to pass a dropout_param dictionary to each
# dropout layer so that the layer knows the dropout probability and the mode
# (train / test). You can pass the same dropout_param to each dropout layer.
self.dropout_param = {}
if self.use_dropout:
self.dropout_param = {"mode": "train", "p": dropout_keep_ratio}
if seed is not None:
self.dropout_param["seed"] = seed
# With batch normalization we need to keep track of running means and
# variances, so we need to pass a special bn_param object to each batch
# normalization layer. You should pass self.bn_params[0] to the forward pass
# of the first batch normalization layer, self.bn_params[1] to the forward
# pass of the second batch normalization layer, etc.
self.bn_params = []
if self.normalization == "batchnorm":
self.bn_params = [{"mode": "train"} for i in range(self.num_layers - 1)]
if self.normalization == "layernorm":
self.bn_params = [{} for i in range(self.num_layers - 1)]
# Cast all parameters to the correct datatype.
for k, v in self.params.items():
self.params[k] = v.astype(dtype)
loss
题面



跟之前也差不了太多,就是计算loss和梯度,一步一步来就是了
解析
因为目前我们还用不上batchnorm,所以我就先不写batchnorm了,分解工作量
看代码注释就好了
代码
def loss(self, X, y=None):
"""Compute loss and gradient for the fully connected net.
Inputs:
- X: Array of input data of shape (N, d_1, ..., d_k)
- y: Array of labels, of shape (N,). y[i] gives the label for X[i].
Returns:
If y is None, then run a test-time forward pass of the model and return:
- scores: Array of shape (N, C) giving classification scores, where
scores[i, c] is the classification score for X[i] and class c.
If y is not None, then run a training-time forward and backward pass and
return a tuple of:
- loss: Scalar value giving the loss
- grads: Dictionary with the same keys as self.params, mapping parameter
names to gradients of the loss with respect to those parameters.
"""
X = X.astype(self.dtype)
mode = "test" if y is None else "train"
# Set train/test mode for batchnorm params and dropout param since they
# behave differently during training and testing.
if self.use_dropout:
self.dropout_param["mode"] = mode
if self.normalization == "batchnorm":
for bn_param in self.bn_params:
bn_param["mode"] = mode
scores = None
############################################################################
# TODO: Implement the forward pass for the fully connected net, computing #
# the class scores for X and storing them in the scores variable. #
# #
# When using dropout, you'll need to pass self.dropout_param to each #
# dropout forward pass. #
# #
# When using batch normalization, you'll need to pass self.bn_params[0] to #
# the forward pass for the first batch normalization layer, pass #
# self.bn_params[1] to the forward pass for the second batch normalization #
# layer, etc. #
############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# 我们网络的结果是这样的 {affine - [batch/layer norm] - relu - [dropout]} x (L - 1) - affine - softmax
# 用一个变量保存上一层的输出
layer_input = X
caches = {}
# 对前面 L - 1层进行操作,因为最后一层的操作和前面的不一样
for i in range(1, self.num_layers):
W = self.params['W' + str(i)]
b = self.params['b' + str(i)]
# 计算affine层的输出
affine_out, affine_cache = affine_forward(layer_input, W, b)
# 计算relu层的输出
relu_out, relu_cache = relu_forward(affine_out)
# 保存cache
caches['affine_cache' + str(i)] = affine_cache
caches['relu_cache' + str(i)] = relu_cache
# 更新layer_input
layer_input = relu_out
# 最后一层的操作
W = self.params['W' + str(self.num_layers)]
b = self.params['b' + str(self.num_layers)]
scores, affine_cache = affine_forward(layer_input, W, b)
caches['affine_cache' + str(self.num_layers)] = affine_cache
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
############################################################################
# END OF YOUR CODE #
############################################################################
# If test mode return early.
if mode == "test":
return scores
loss, grads = 0.0, {}
############################################################################
# TODO: Implement the backward pass for the fully connected net. Store the #
# loss in the loss variable and gradients in the grads dictionary. Compute #
# data loss using softmax, and make sure that grads[k] holds the gradients #
# for self.params[k]. Don't forget to add L2 regularization! #
# #
# When using batch/layer normalization, you don't need to regularize the #
# scale and shift parameters. #
# #
# NOTE: To ensure that your implementation matches ours and you pass the #
# automated tests, make sure that your L2 regularization includes a factor #
# of 0.5 to simplify the expression for the gradient. #
############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# 计算loss
loss, dscores = softmax_loss(scores, y)
# 先计算最后一层的梯度
W = self.params['W' + str(self.num_layers)]
affine_cache = caches['affine_cache' + str(self.num_layers)]
d_relu_out, dW, db = affine_backward(dscores, affine_cache)
grads['W' + str(self.num_layers)] = dW + self.reg * W
grads['b' + str(self.num_layers)] = db
# 计算前面的梯度
for i in range(self.num_layers - 1, 0, -1):
W = self.params['W' + str(i)]
affine_cache = caches['affine_cache' + str(i)]
relu_cache = caches['relu_cache' + str(i)]
# 先计算relu层的梯度
d_affine_out = relu_backward(d_relu_out, relu_cache)
# 再计算affine层的梯度
d_relu_out, dW, db = affine_backward(d_affine_out, affine_cache)
# 保存梯度
grads['W' + str(i)] = dW + self.reg * W
grads['b' + str(i)] = db
# 加上正则化项
for i in range(1, self.num_layers + 1):
W = self.params['W' + str(i)]
loss += 0.5 * self.reg * np.sum(W * W)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
############################################################################
# END OF YOUR CODE #
############################################################################
return loss, grads
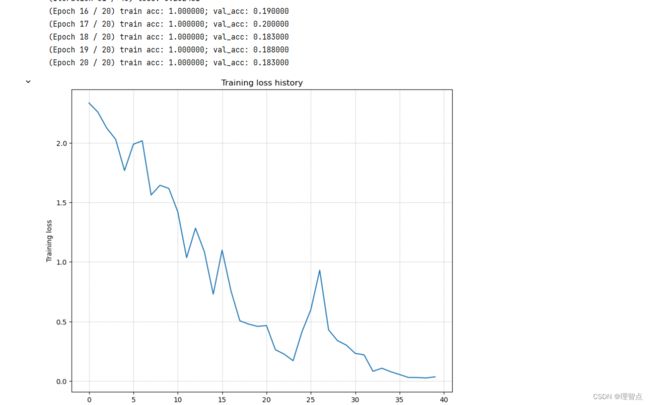
输出
调整一个三层神经网络使其过拟合
题面
解析
学习率对于拟合效果的影响我就不赘述了,说一下Weight_scale对拟合效果的影响吧
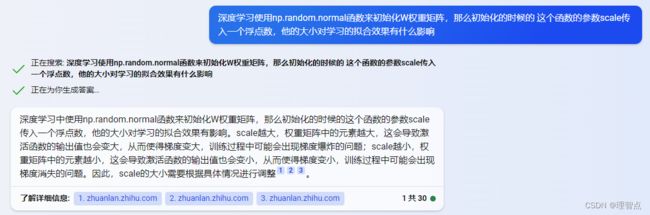
没啥好说的,调参!
结果
有好几种方法,我随便列几个
weight_scale = 1e-2 # Experiment with this!
learning_rate = 1e-2 # Experiment with this!
weight_scale = 3e-2 # Experiment with this!
learning_rate = 4e-3 # Experiment with this!
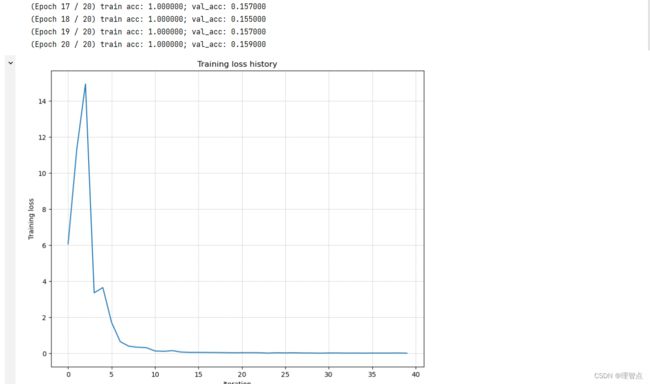
调整一个五层神经网络使其过拟合
结果
weight_scale = 4e-2 # Experiment with this!
learning_rate = 1e-2 # Experiment with this!
Inline Question 1
题面
![]()
粗浅的翻译就是三层网络和五层网络哪个训练起来更难?那个网络对weight_scale更敏感
答案
如果你自己调试过,就会发现五层网络更难
因为他的准确率更加依赖于初始化,所以他对weight_scale更敏感
update_rules
接下来一部分就是让我们来实现参数更新的规则的视线,除了最基础的梯度下降,还有几个新学的更新算法,具体的可以看这个网站https://cs231n.github.io/neural-networks-3/#sgd
sgd_momentum
题面
解析
代码
def sgd_momentum(w, dw, config=None):
"""
Performs stochastic gradient descent with momentum.
config format:
- learning_rate: Scalar learning rate.
- momentum: Scalar between 0 and 1 giving the momentum value.
Setting momentum = 0 reduces to sgd.
- velocity: A numpy array of the same shape as w and dw used to store a
moving average of the gradients.
"""
if config is None:
config = {}
config.setdefault("learning_rate", 1e-2)
config.setdefault("momentum", 0.9)
v = config.get("velocity", np.zeros_like(w))
next_w = None
###########################################################################
# TODO: Implement the momentum update formula. Store the updated value in #
# the next_w variable. You should also use and update the velocity v. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
v = config["momentum"] * v - config["learning_rate"] * dw
next_w = w + v
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
config["velocity"] = v
return next_w, config
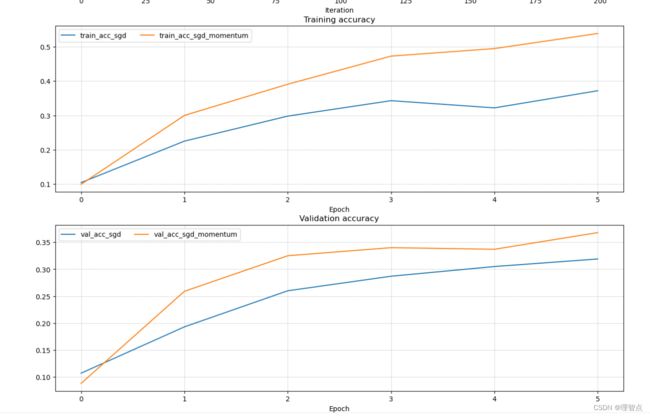
输出
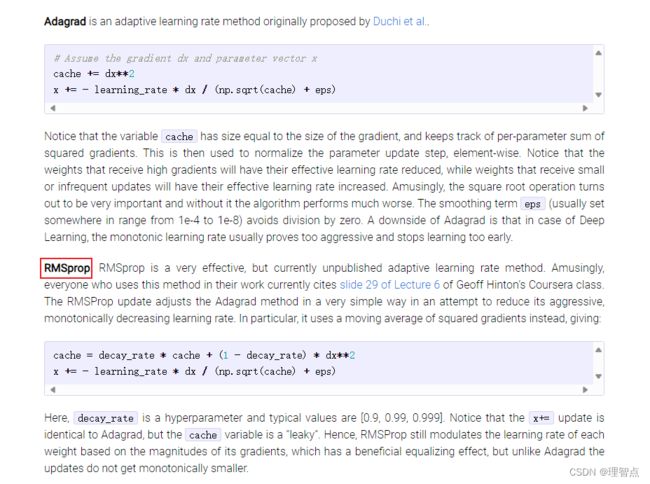
RMSProp
题面
解析
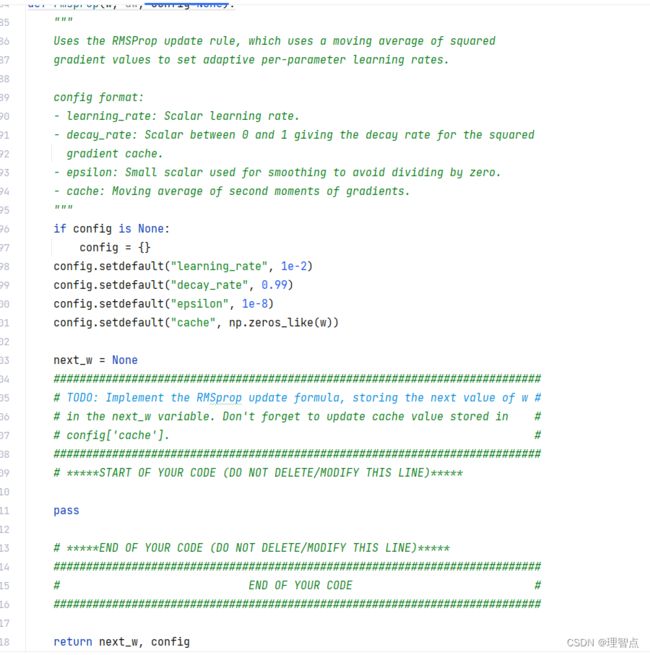
代码
def rmsprop(w, dw, config=None):
"""
Uses the RMSProp update rule, which uses a moving average of squared
gradient values to set adaptive per-parameter learning rates.
config format:
- learning_rate: Scalar learning rate.
- decay_rate: Scalar between 0 and 1 giving the decay rate for the squared
gradient cache.
- epsilon: Small scalar used for smoothing to avoid dividing by zero.
- cache: Moving average of second moments of gradients.
"""
if config is None:
config = {}
config.setdefault("learning_rate", 1e-2)
config.setdefault("decay_rate", 0.99)
config.setdefault("epsilon", 1e-8)
config.setdefault("cache", np.zeros_like(w))
next_w = None
###########################################################################
# TODO: Implement the RMSprop update formula, storing the next value of w #
# in the next_w variable. Don't forget to update cache value stored in #
# config['cache']. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
cache = config["cache"]
cache = config["decay_rate"] * cache + (1 - config["decay_rate"]) * dw ** 2
next_w = w - config["learning_rate"] * dw / (np.sqrt(cache) + config["epsilon"])
config["cache"] = cache
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return next_w, config
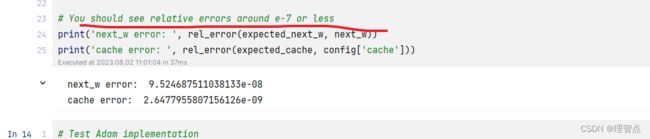
输出
Adam
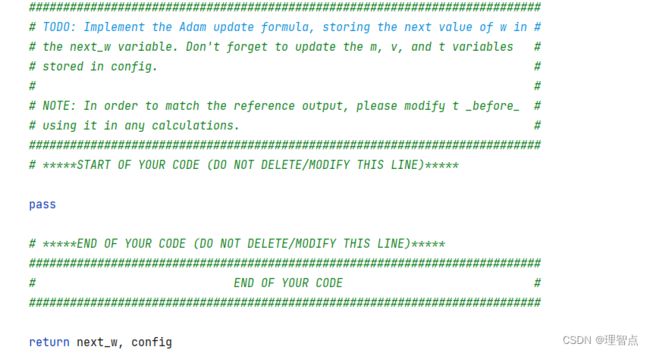
题面
解析
代码
def adam(w, dw, config=None):
"""
Uses the Adam update rule, which incorporates moving averages of both the
gradient and its square and a bias correction term.
config format:
- learning_rate: Scalar learning rate.
- beta1: Decay rate for moving average of first moment of gradient.
- beta2: Decay rate for moving average of second moment of gradient.
- epsilon: Small scalar used for smoothing to avoid dividing by zero.
- m: Moving average of gradient.
- v: Moving average of squared gradient.
- t: Iteration number.
"""
if config is None:
config = {}
config.setdefault("learning_rate", 1e-3)
config.setdefault("beta1", 0.9)
config.setdefault("beta2", 0.999)
config.setdefault("epsilon", 1e-8)
config.setdefault("m", np.zeros_like(w))
config.setdefault("v", np.zeros_like(w))
config.setdefault("t", 0)
next_w = None
###########################################################################
# TODO: Implement the Adam update formula, storing the next value of w in #
# the next_w variable. Don't forget to update the m, v, and t variables #
# stored in config. #
# #
# NOTE: In order to match the reference output, please modify t _before_ #
# using it in any calculations. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
t = config["t"] + 1
m = config["beta1"] * config["m"] + (1 - config["beta1"]) * dw
mt = m / (1 - config["beta1"] ** t)
v = config["beta2"] * config["v"] + (1 - config["beta2"]) * dw ** 2
vt = v / (1 - config["beta2"] ** t)
next_w = w - config["learning_rate"] * mt / (np.sqrt(vt) + config["epsilon"])
config["t"] = t
config["m"] = m
config["v"] = v
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return next_w, config
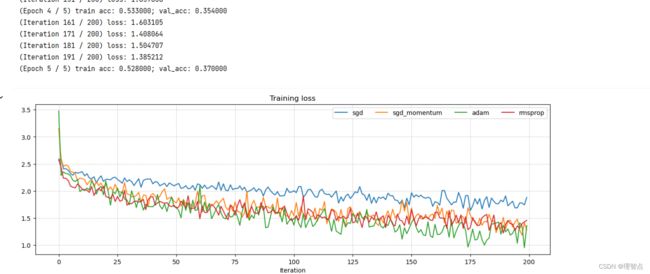
输出
train you best model
题面
解析
没啥好说的
代码
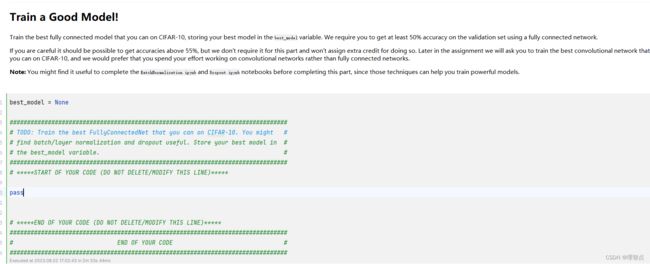
best_model = None
################################################################################
# TODO: Train the best FullyConnectedNet that you can on CIFAR-10. You might #
# find batch/layer normalization and dropout useful. Store your best model in #
# the best_model variable. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
best_val = -1
best_params = {}
# 重新定义一下训练数量
num_train = 500
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
#随机训练30次,每次随机生成学习率和正则化强度,先用小数据集训练一下
for i in range(30):
lr = 10 ** np.random.uniform(-5, -3) # 学习速度
ws = 10 ** np.random.uniform(-3, -1) # 权重缩放
reg = 10 ** np.random.uniform(-3, -1) # 正则化强度
# 创建一个四层模型
model = FullyConnectedNet([256, 128, 64],
weight_scale=ws,
reg=reg)
# 使用adam更新策略
solver = Solver(model, small_data,
num_epochs=20, batch_size=256,
update_rule='adam',
optim_config={
'learning_rate': lr,
},
verbose=False)
solver.train()
new_val = solver.best_val_acc
if new_val > best_val:
best_val = new_val
best_model = model
best_params['lr'] = lr
best_params['reg'] = reg
best_params['ws'] = ws
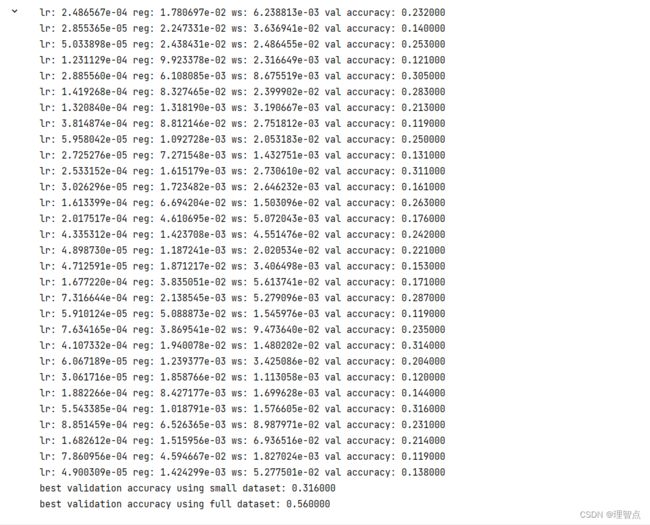
print('lr: %e reg: %e ws: %e val accuracy: %f' % (
lr, reg, ws, new_val))
print('best validation accuracy using small dataset: %f' % best_val)
# 拿效果最好的参数训练全部数据
best_model = FullyConnectedNet([256, 128, 64, 32],
weight_scale=best_params['ws'],
reg=best_params['reg'])
solver = Solver(best_model, data,
num_epochs=20, batch_size=256,
update_rule='adam',
optim_config={
'learning_rate': best_params['lr'],
},
verbose=False)
solver.train()
print('best validation accuracy using full dataset: %f' % solver.best_val_acc)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################