深入了解Lasso+Jolt

1. 引言

前序博客有：

• Lasso、Jolt 以及 Lookup Singularity——Part 1
• Lasso、Jolt 以及 Lookup Singularity——Part 2

相关论文见：

• Srinath Setty（微软研究中心）、Justin Thaler（a16z密码学研究中心以及Georgetown University）、Riad Wahby（Carnegie Mellon University）2023年论文《Unlocking the lookup singularity with Lasso》
• Arasu Arun（New York University）、Srinath Setty（微软研究中心）、Justin Thaler（a16z密码学研究中心以及Georgetown University）2023年论文《Jolt: SNARKs for Virtual Machines via Lookups》

相应的开源代码实现见：

• https://github.com/a16z/Lasso（Rust）

本文总体结构为：

• 何为lookup arguments？
• 何为Lasso/Jolt？
• Lasso细节
• Jolt细节
• 如何将Lasso看成是工具？
  • 以及，lookup argument在zkVM之外的应用场景？

2. 何为lookup arguments？

lookup arguments可分为：

• 1）Unindexed lookup argument：
  • 为subset relation proof，即，batch set-membership proof—— $a$为table $t$的某subset。
• 2）Indexed lookup argument：【Lasso和Jolt使用的是indexed lookup argument】
  • 为对只读内存的读取。可将$t$看成是内存，$a_i=t[b_i]$表示读取$b_i$内存单元中的值。

以range check为例，lookup argument是指：

• 1）令$t=(0,1,2,3,\cdots ,2^{128}-1)$为具有$N$个table元素的向量（即$t$为pre-determined table）。
• 2）令$a\in {\mathbf{F}}^m$为一组应包含在上述table的值列表。
• 3）Verifier $V$已知：$a$的承诺值$c{m}_a$。
• 4）Prover $P$声称：$a$中所有元素均在table $t$中。
  即Prover $P$声称其知道$c{m}_a$的opening $a$，使得：
  • 对于每个$i=0,\cdots ,m-1$，存在某index $b_i\in \{0,1,\cdots ,N-1\}$，使得$a_i=t[b_i]$。
• 5）通常将这种lookup argument称为unindexed lookup argument。

而indexed lookup argument是指待证明元素中还附加了索引值，indexed lookup argument定义为：【Verifier知道table $t$的succinct描述。】

• 1）令$t\in {\mathbf{F}}^n$为具有$N$个table元素的向量（即$t$为pre-determined table）。
• 2）Prover $P$对向量$((a_1,b_1),\cdots ,(a_m,b_m))$进行承诺。
• 3）Prover $P$声称，对于$i=1,\cdots ,m$，有$a_i=t[b_i]$。【即$a_i$为value，$b_i$对应为table $t$的索引号，Prover $P$声称$a$中所有元素均存在于$t$中相应的index。】

3. 何为Lasso/Jolt？

Lasso：为一组（indexed）lookup argument：

• Lasso Prover $P$的速度要比之前的方案快一个量级。
  • Prover $P$的关键瓶颈在于：承诺开销。
• Lasso Prover $P$对更少的field elements进行commit，且所有这些待承诺的field elements都是small的。
• No commitment to $t$ needed for many tables。【对于（Jolt中需要的）大量的lookup tables，无需honest party来对table进行 commit和预处理。基于Lasso的Verifier可自行处理巨大table（仅需约50/100/200个field运算），而不是接收table的承诺值。】
• 支持巨大tables（可分解，或LDE-structured）：
  • Prover $P$的承诺开销为：$O(c(m+N^{1/c}))$个field elements。
  • 将table分解主要有2方面的Prover开销，通常取$c=6$来对这2方面开销进行平衡：
    • 仅依赖于table size的开销
    • 仅依赖于lookup次数的开销

Jolt：为新的zkVM技术：

• Jolt Prover $P$的承诺开销要比之前的方案低得多。
• 通过对单个指令的整个evaluation table的一次lookup，来实现Primitive instruction。

4. Lasso细节

4.1 Lasso开销细节

对size为$N$、具有参数$c$的table，做$m$次indexed lookup：

• Lasso Prover $P$开销为：对$3cm+c{N}^{1/c}$个field elements进行commit。
  • 所有field elements都是small的，即在set $\{0,1,\cdots ,m\}$中：
    • 基于MSM的多项式承诺方案，Lasso Prover $P$对每个（small）committed field element，仅需要约做1次group 运算。
      目前基于MSM的多项式承诺方案有：
      • KZG-based多项式承诺方案
      • IPA/Bulletproofs多项式承诺方案
      • Hyrax多项式承诺方案
      • Dory多项式承诺方案
• Lasso Verifier $V$开销为：
  • $O(\log m)$次field运算 和 hash evaluations（from Fiat-Shamir）。
  • ＋ 1个evaluation proof for a committed polynomial of size $N^{1/c}$。
  • 通过composition/recursion，可将以上足够低的 Lasso Verifier $V$开销 进一步reduce。

当$c=1$时，对应的为Lasso的特例情况——Basic-Lasso：

• Basic-Lasso Prover $P$对$m+N$个field elements进行commit。
• 这$m+N$个field elements中，有很多为0值。在MSM-based多项式承诺方案中，对0值进行commit的开销也为0，即“free”。
• 这$m+N$个field elements中，最多有$2m$个为非零值：
  • 若每次读取的为不同的table cell，则有$m$个field elements为1，其它的均为0。

4.2 将Lasso用于巨型table：$c>1$

实际上，大多数大型lookup table都是可分解的：

• 可将对大型size为$N$的table的一次lookup，分解为，对size为$N^{1/c}$的table的约$c$次lookup，然后"整理（collating）"这$c$个lookup的结果 ：
  • Lasso使用sum-check protocol来"整理"这$c$个lookup的结果。因此对Lasso Prover $P$来说，没有额外的承诺开销。

可将Lasso看成是$c>1$，将对单个大型、可分解table的lookup，reduce为，对多个small tables的$c$个lookup：

• 对small tables，可使用任意lookup argument。
  • 对于small tables，Lasso中使用Basic-Lasso lookup argument方案。
• 附加说明：small-table lookup argument必须是indexed。
• 目前已知的方案来将unindexed lookup argument 转换为 indexed lookup argument。
  • 但是，这些已知方案要么无法保留table entries的“smallness”，要么无法保留big table的可分解性——原因在于，这些方案将indices和values "pack"为了单个field element。

【proof size不取决于不同table的数量，也不取决于small table的size。Verifier需在某random point上 evaluate每个small table的 multi-linear extension polynomial，small tables数量的增加会引起Verifier time的增加，但这些都是field运算，相比于其它密码学操作来说，这不会成为Verifier的瓶颈。
Jolt中有约45种不同的subtables。
】

4.3 背景知识：Grand Product Arguments

所有已知的lookup argument都采用了grand product argument：

• grand product argument是一种SNARK方案，用于证明$n$个committed values的乘积。
• 当今流行的grand product argument，其Prover $P$需额外再对$n$个值（partial products）进行commit。
• 这是没必要的。
• T13论文中：给出了GKR protocol的优化版本（所谓GKR protocol，为sum-check-based interactive proof for circuit evaluation）：【对类似于binary tree of multiplication gates的电路进行了优化。】
  • Prover $P$无承诺开销。
  • Prover $P$做线性次数的field运算。
  • Proof size/Verifier $V$ time为$O(\log (n{)}^2)$次field运算（以及hash evaluations from Fiat-Shamir）：
    • 远少于FRI的Proof size/Verifier $V$ time。
    • [Lee, Setty 2019]中将Verifier $V$开销进一步reduce为约$O(\log (n))$，只需增加Prover $P$的一点点承诺开销。

4.4 Basic-Lasso关键点

• 对于很多现有的lookup arguments，若swap out the invoked grand product argument for T13，则Prover $P$仅需对small field elements进行commit。
  • 详细可参看Ulrich Hab¨ock的 logUp-Multivariate lookups based on logarithmic derivatives：借助对数导数，将grand product argument 转换为了 grand sum argument。
  • More involved than just a simple swap of a grand product argument。
• Lasso/Jolt需要使用indexed lookup argument，来将small-table lookup results “collating” into big-table results。
• 技术卖点：当前社区仍未充分利用sum-check的潜力来避免Prover $P$的开销。
• 关于Basic-Lasso的工作原理，可参看：
  • Lasso、Jolt 以及 Lookup Singularity——Part 2

5. Jolt细节

当前VM execution的前端（front-end）：

• Prover $P$声称运行某computer program for $m$ steps：
  • 该程序以某VM的汇编语言来编写。
  • 流行的VM面向目标有：RISC-V、Ethereum Virtual Machine（EVM）。
• 当前，前端为每个computation step生成一个电路：
  • 步骤1：指出在该step应执行哪个指令。
  • 步骤2：执行该指令。
• 而Lasso将上面的 步骤2 替换为 a single lookup：
  • 对于每个指令，该table中存储了该指令的整个evaluation table。
  • 若指令$f$有2个64-bit输入，则对于每个64-bit input pair $(x,y)$，lookup table会存储所有的$f(x,y)$：
    • 该lookup table size为$2^{128}$。
    • Jolt中展示了，所有的RISC-V指令都是可分解的。

Jolt概览图为：

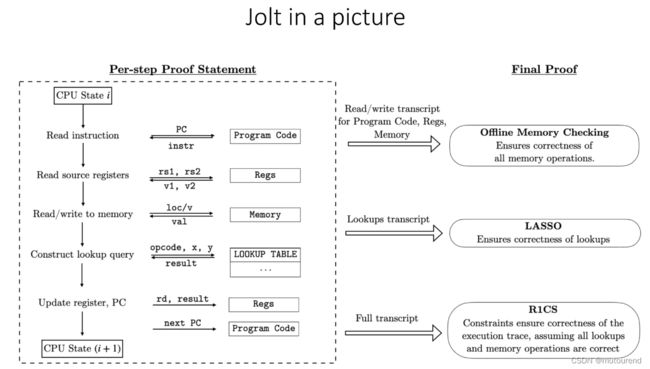
Jolt有望实现Barry Whitehat的Lookup Singularity愿景：

• 具有易审计、简单化、可扩展性等优势
• 性能优势
• 本质不同的构建zkVM的方式：
  • 与人们现有在做的事情有很多相似之处。
  • 人们愿景将类似bitwise-AND这样的计算函数转换为 对small tables的多次lookup，并将结果合并。
  • Jolt的关键不同之处在于：
    • a）新的small-table lookup argument具有快得多的Jolt Prover $P$。
    • b）新的small-table lookup argument为天然indexed。
    • c）Jolt Prover $P$具有快得多的collating技术：
      • 可对small-table lookup results进行“Free” multiply和add。
  • Jolt的这些不同之处，使得可借助lookup 来实现VM emulation中的almost everything。

5.1 Jolt分解示例1——Bitwise-AND

对于有2个64-bit输入$x,y$的bitwise-AND原酸，其分解思路为：

• 将$x,y$分解为$c=8$个chunks，每个chunk有8 bit。
• 计算每个chunk的bitwise-AND
• 将各chunk结果拼接起来，即输出为：
  ${\sum }_{i=1}^8{8}^{i-1}\cdot \text{bitwiseAND}(x_i,y_i)$

为避免需要honest-party来对sub-table进行commit：

• $\text{bitwiseAND}(x_i,y_i)={\sum }_{j=1}^8{2}^{j-1}\cdot x_j\cdot y_j$为multilinear多项式，可 以少于25个field运算来evaluate。
• Lasso Verifier $V$需要知道该sub-table，转为，只需要知道该多项式的一个evaluation。

5.2 Jolt分解示例2——RISC-V Addition

对2个64-bit number $x,y$ 求和，RISC-V规定其相加正确，并忽略任意“overflow bit”。

Jolt（通过对ancillary R1CS添加一个约束来）在有限域内计算$z=x+y$，然后使用lookup来标识相应的overflow bit，若有overflow bit，则据此调整相应的结果。

• Jolt Prover $P$，对field element $z=x+y$的“limb-decomposition” $(b_1,\cdots ,b_c)$进行commit。
• 令$M=2^{64/c}$为每个limb的最大值。
• 向R1CS添加一个约束，以确认：
  • 步骤1：$z={\sum }_{j=1}^c{M}^{j-1}\cdot b_j$
  • 步骤2：并对每个$b_j$通过lookup into 存储了$\{0,\cdots ,M-1\}$的subtable，来做range check。
• 通过以上约束的步骤1和步骤2，就可确保$b_1,\cdots ,b_j$确实为$z$的规定的limb-decomposition。
• 为识别overflow bit，仅需要做a lookup at index $b_c$, into a table whose $i$’th entry spits out the relevant high-order bit of $i$。

5.3 Jolt分解示例2——LESS THAN UNSIGNED

对2个64-bit输入$x,y$做less than运算：

• 将$x,y$分解为$c=8$个chunks，每个chunk有8 bit。
• 计算每个chunk的LESS-THAN(LT) 和 EQUALITY(EQ)
• 输出为：${\sum }_{i=1}^8{2}^{i-1}\cdot \text{LT}(x_i,y_i){\prod }_{j=i+1}^8\text{EQ}(x_j,y_j)$

为避免对2个sub-table进行commit：

• $\text{EQ}(x_j,y_j)={\prod }_{k=1}^8(x_{j,k}{y}_{j,k}+(1-x_{j,k})(1-y_{j,k}))$
• $\text{LT}(x_i,y_i)={\sum }_{k=1}^8(1-x_i)y_i{\prod }_{z=k}^8(x_{i,k}{y}_{i,k}+(1-x_{i,k})(1-y_{i,k}))$
• 这些均为multilinear多项式，可 以少于50个filed运算来evaluate。

6. 如何将Lasso看成是工具？以及，lookup argument在zkVM之外的应用场景？

6.1 Lasso as a tool的直觉

• Lasso支持对field element的bit-decompositions的简单运算，无需Lasso Prover $P$对各个bit进行commit。
• sub-tables具有quickly-evaluable multilinear extension，若每个sub-table对应a simple function on the (bits of) the table indices：
  • 从而可确保无需honest party在预处理时对这些sub-tables进行commit。
• 对2个field elements取值为$\{0,1,\cdots ,2^{64}-1\}$的bitwiseAND运算，相比于Plonk中每个加法或乘法门的开销，Lasso Prover 开销更低。
• 注意：Lookup arguments为规模经济。适于do many lookups into one table（即对同一函数的多次调用）。

6.2 将indexed lookup arguments看成是repeated function evaluation的SNARKs方案

之前有很多关于“SNARKs for repeated function evaluation”的研究：

• 基于很多不同输入$x_1,\cdots ,x_m$，计算同一函数$f$。
• 可将其看成是“polynomial” amount of data parallelism：
  • 若函数$f$的输入长度为$n$，则不同输入的数量为$m=\text{poly}(n)$。
• 仍要求Prover $P$ evaluate $f$ in a very specific way：
  • Executing a specific circuit to compute $f$。

看待lookup arguments新视角：

• 将lookup table看成是存储了某函数$f$的所有evaluations
• lookup argument则为a SNARK for highly repeated evaluation of $f$：
  • 令Prover证明，committed vector $((a_1,f(a_1)),\cdots ,(a_m,f(a_m)))$，中包含了对不同输入$a_1,\cdots ,a_m$的正确$f$ evaluations。
• Lasso Prover $P$的开销为$O(c(m+N^{1/c}))$，当lookup次数$m$ 不比 table size $N$，小太多时，Lasso Prover $P$是高效的：
  • 即运行$f$的次数 应为 exponential in the input size of $f$。

7. 小结

• Lasso适于对同一函数evaluate很多次的场景。
• zkVM只是Lasso的应用场景之一：
  • 根据定义，VM抽象表示的是对primitive指令的重复执行的计算。
  • 实现VM抽象通常具有大量的性能开销。
• 未来感兴趣的方向：
  • 隔离计算中重复结构的其它更好方式
  • 示例工作有：
    • Bit-slicing
    • evaluate 哈希函数或block cipher（如SHA/AES），可构建具有64个不同输入的Boolean circuit $C$来计算：
      • 将每个输入的第一个bit pack进a single field element，将每个输入的第二个bit pack进a single field element，以此类推。
      • 将circuit $C$中的每个AND 门，替换为bitwiseAND；将circuit $C$中的每个OR 门，替换为bitwiseOR等等。
      • circuit $C$中每个gate的output为SHA/AES所有64 evaluations的one bit。
      • 对circuit $C$运用Lasso。

参考资料

[1] Justin Thaler 2023年8月在zkStudyClub视频分享 zkStudyClub - Lasso/Jolt (Justin Thaler, Georgetown University/a16z)
相应slide见：zkStudyClub - Lasso/Jolt (Justin Thaler, GWU/a16z)

Justin Thaler系列博客

• SNARK Design
• Rollup项目的SNARK景观
• SNARK原理示例
• SNARK性能及安全——Prover篇
• SNARK性能及安全——Verifier篇
• sum-check protocol in zkproof
• sum-check protocol深入研究
• Lasso、Jolt 以及 Lookup Singularity——Part 1
• Lasso、Jolt 以及 Lookup Singularity——Part 2

lookup系列博客

• PLOOKUP
• PLOOKUP代码解析
• Efficient polynomial commitment schemes for multiple points and polynomials学习笔记
• PLONK + PLOOKUP
• PlonKup: Reconciling PlonK with plookup
• PLONK: permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge 学习笔记
• Plonk代码解析
• RapidUp: Multi-Domain Permutation Protocol for Lookup Tables学习笔记
• Lookup argument总览
• Halo2 学习笔记——设计之Proving system之Lookup argument（1）
• logUp-Multivariate lookups based on logarithmic derivatives
• cq：fast lookup argument
• Lookup Argument性能优化——Caulk
• 2023年 ZK Hack以及ZK Summit 亮点记
• Research Day 2023：Succinct ZKP最新进展
• Lasso、Jolt 以及 Lookup Singularity——Part 1
• Lasso、Jolt 以及 Lookup Singularity——Part 2