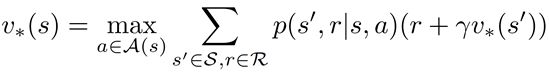深度强化学习。介绍。深度 Q 网络 （DQN） 算法

马库斯·布赫霍尔茨

一. 引言

        深度强化学习的起源是纯粹的强化学习，其中问题通常被框定为马尔可夫决策过程（MDP）。MDP 由一组状态 S 和操作 A 组成。状态之间的转换使用转移概率 P、奖励 R 和贴现因子 gamma 执行。概率转换P（系统动力学）反映了从一个状态到另一个状态的不同转换和奖励发生的次数，其中顺序状态和奖励仅取决于在前一个时间步采取的状态和操作。

        强化学习定义了代理执行某些操作（根据策略）以最大化奖励的环境。代理最优行为的基础由贝尔曼方程定义，贝尔曼方程是解决实际优化问题的广泛使用的方法。为了求解贝尔曼最优方程，我们使用动态规划。

        当代理存在于环境中并过渡到另一个状态（位置）时，我们需要估计状态 V（s）（位置）的值 — 状态值函数。一旦我们知道每个状态的值，我们就可以弄清楚什么是最好的方法来操作 Q（S， A） — 动作值函数（只需遵循具有最高值的状态）。

        这两个映射或函数非常相互关联，可以帮助我们找到

        针对我们问题的最佳策略。我们可以表示，状态值函数告诉我们，如果代理遵循策略π，处于状态 S 有多好。

符号的含义如下：

E[X] — 随机变量 X 的期望

π — 政策

Gt — 时间 t 的折扣回报

γ — 贴现率

但是，操作值函数 q （s， a） 是从状态 S 开始，执行操作 A 并遵循策略π的预期回报，并告诉我们从特定状态执行特定操作有多好，

值得一提的是，状态值函数和 Q 函数之间的区别在于，值函数指定状态的好坏，而 Q 函数指定状态中动作的好坏。

MDP由贝尔曼方程求解，该方程以美国数学家理查德·贝尔曼的名字命名。该等式有助于找到最佳策略和价值函数。代理根据强加的策略（策略 — 正式地，策略定义为每个可能状态的操作的概率分布）来选择操作。代理可以遵循的不同策略意味着状态的不同值函数。但是，如果目标是最大化收集的奖励，我们必须找到最佳策略，称为最佳策略。

        另一方面，最优状态值函数是与所有其他值函数（最大回报）相比具有更高值的函数，因此最优值函数也可以通过取 Q 的最大值来估计：

        最后，值函数的贝尔曼方程可以表示为：

        类似地，Q 函数的贝尔曼方程可以表示如下：

        基于最优状态值函数和上述状态值函数动作-值函数方程，我们可以安排最优值函数的最终方程，称为贝尔曼最优方程：

        通常，强化学习问题是使用 Q — 学习算法来解决的。在这里，如上所述，代理与环境交互并获得奖励。目标是制定最佳政策（行动选择策略）以最大化奖励。在学习过程中，代理更新 Q（S，A） 表（终止在剧集结束时完成 — 达到目标）。

        Q — 学习算法按照以下步骤执行：

        1. 使用随机值初始化表 Q（S，A）。

        2. 对 epsilon 采取行动 （A） — 贪婪的政策并移动到下一个状态 S'

        3. 按照更新公式更新先前状态的 Q 值：

        最好的开始方法是从OpenAI健身房解决冰冻湖环境。

        在冰冻湖环境中（请熟悉OpenAI描述），代理可以停留在16个状态并执行4个不同的操作（在一个状态中）。在本例中，我们的 Q（S，A） 表的大小为 16 x 4。

        冰冻湖的代码可以如下：

import gym
import numpy as np
import random
env = gym.make('FrozenLake-v0')

'''
While we choose the Action to take, we follow the epsilon-greedy policy: we either explore for new actions with a
probability epsilon or take an action which has a maximum value with a probability 1-epsilon. While updating the Q value, 
we simply select the action that has a maximum value + noise
'''

def epsilon_greedy_policy(state, epsilon, i):
    if random.uniform(0,1) < epsilon:
        return env.action_space.sample()
    else:
        return np.argmax(Q[state,:] + np.random.randn(1,env.action_space.n)*epsilon)
        
Q = np.zeros([env.observation_space.n, env.action_space.n])

# Definitiion of learning hyperparameters
ALPHA = 0.1
GAMMA = 0.999
NUMBER_EPISODES = 3000
epsilon = 0.015


total_REWARDS = []
for i in range(NUMBER_EPISODES):
    #Reset environment. Get first state.
    state = env.reset()
    sum_reward = 0
    done = False
    j = 0
    #The Q-Table learning algorithm
    while True:

        action = epsilon_greedy_policy(state, epsilon, i)
        #Get new state and reward from environment
        state_next, reward, done, _ = env.step(action)
        #Q table UPDATE
        Q[state,action] = Q[state,action] + ALPHA * (reward + GAMMA * np.max(Q[state_next,:]) - Q[state,action])
        
        sum_reward += reward
        state = state_next
        if done == True:
            break

    
    total_REWARDS.append(sum_reward)


print ("--- Q[S,A]-Table ---")
print (Q)

        请注意，上面给出的Q -算法属于时间差分学习算法（Richard S. Sutton于1988年）。Q — 算法是一种关闭的 — 策略算法（作为方法学习旧历史数据的能力）。Q — 学习算法的扩展是一种 SARSA（上 — 策略算法。唯一的区别是 Q（S，A） 表更新：

二. 深度强化学习（深度 Q — 网络 — DQN）

        强化学习可以充分适用于可以管理（迭代）所有可实现状态并将其存储在标准计算机RAM内存中的环境。然而，在状态数量超过当代计算机容量的环境中（对于雅达利游戏，有12833600状态），标准的强化学习方法不是很适用。此外，在实际环境中，代理必须面对连续状态（非离散）、连续变量和连续控制（动作）问题。

        考虑到代理必须操作的环境的复杂性（状态数，连续控制），标准明确定义的强化学习Q - 表被深度神经网络（Q - 网络）取代，深度神经网络（Q - 网络）将（非线性近似）环境状态映射到代理操作。网络架构、网络超参数的选择和学习在训练阶段进行（学习 Q — 网络权重）。
DQN允许代理探索非结构化环境并获得知识，随着时间的推移，这些知识使它们有可能模仿人类行为。

三、 学习算法 DQN

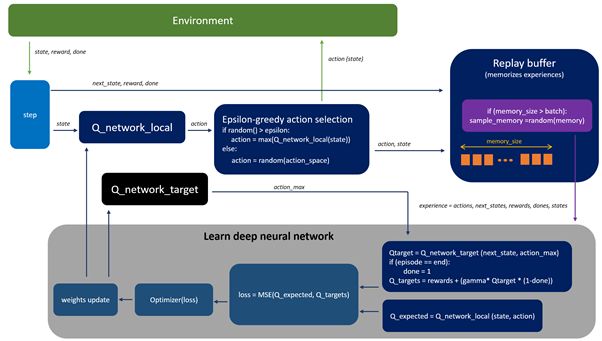
        下图（在训练过程中）描述了DQN的主要概念，其中Q — 网络作为非线性近似进行，将两种状态映射到一个动作值中。

        在训练过程中，代理与环境交互并接收数据，这些数据在学习 Q — 网络期间使用。代理探索环境以构建转换和操作结果的完整图景。一开始，代理随机决定随着时间的推移变得不足的操作。在探索环境时，代理尝试查看 Q — 网络（近似）以决定如何行动。我们将这种方法（随机行为和根据Q - 网络的组合）称为epsilon - greedy方法（Epsilon - greedy action selection块），它只是意味着使用概率超参数epsilon在随机和Q策略之间切换。

        所提出的Q学习算法的核心来源于监督学习。

        正如上面提到的，目标是用深度神经网络近似一个复杂的非线性函数 Q（S， A）。

类似地，对于监督学习，在 DQN 中，我们可以将损失函数定义为目标值和预测值之间的平方差，并且我们还将尝试通过更新权重来最小化损失（假设代理通过执行一些操作 a 来执行从一个状态 s 到下一个状态 s 的转换并获得奖励 r）。

        在学习过程中，我们使用两个独立的 Q — 网络（Q_network_local 和 Q_network_target）来计算预测值（权重 θ）和目标值（权重 θ'）。目标网络被冻结几个时间步长，然后通过从实际 Q 网络复制权重来更新目标网络权重。将目标 Q — 网络冻结一段时间，然后用实际的 Q 网络权重更新其权重以稳定训练。

图1.DQN 算法概念

        为了使训练过程更加稳定（我们希望避免在相对相关的数据上学习网络，如果我们在连续更新（上次转换）上执行学习，就会发生这种情况），我们应用重放缓冲区来记忆代理行为的体验。然后，对来自重放缓冲区的随机样本进行训练（这降低了代理经验之间的相关性，并帮助代理从广泛的经验中更好地学习）。

        DQN 算法可以描述如下：

        1. 初始化重播缓冲区，

        2. 预处理和环境并将状态 S） 馈送到 DQN，它将返回该状态中所有可能操作的 Q 值。

        3. 使用 epsilon 贪婪策略选择一个动作：使用 epsilon 概率，我们选择一个随机动作 A，概率为 1-epsilon。选择具有最大 Q 值的操作，例如 A = argmax（Q（S， A， θ））。

        4. 选择操作 A 后，代理在状态 S 中执行所选操作并移动到新状态 S' 并获得奖励 R。

        5. 将重播缓冲区中的过渡存储为 。

        6. 接下来，从重放缓冲区中随机采样一些随机批次的转换，并使用公式计算损失：

        7. 根据实际网络参数执行梯度下降，以最大程度地减少这种损失。

        8. 每 k 步后，将我们的实际网络权重复制到目标网络权重。

        9. 对 M 集数重复这些步骤。

四、项目设置。结果。

        在本节中，我将介绍Udacity（深度强化学习）的项目实施结果 - 请查看我的GitHub。

a. 项目目标

在这个项目中，目标是训练代理在方形环境中导航如何收集黄色香蕉。项目要求是在连续 13 集内收集 +100 的平均分数。

b.在导航项目中，应用了神经网络架构和超参数的以下设置：

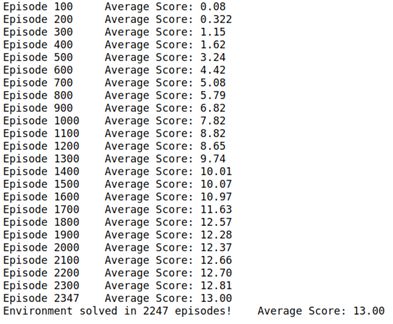
下面描绘的每集奖励图说明了代理在播放 100 集时能够获得至少 +13 的平均奖励（超过 2247 集）。

Q-网络架构：

输入层 FC1：37 个节点输入，64 个节点输出 隐藏层 FC2：64 个节点输入，64 个节点输出 隐藏层 FC3：64 个节点输入，64 个节点输出 输出层：64 个节点输入，4 个输出


— 动作大小

应用的超参数：

BUFFER_SIZE = int（1e5） # 重播缓冲区大小 BATCH_SIZE = 64 # 迷你批量大小

伽玛 = 0.99 # 折扣因子
TAU = 1e-3 # 用于目标参数
的软更新 LR = 5e-4 # 学习率
UPDATE_EVERY = 4 # 更新网络
的频率 厄普西隆开始 = 1.0 厄普西隆开始 = 0.01
厄普西隆衰减 = 0.999

图2.代理学习时的平均分

五、未来工作的想法

        考虑到深度学习的经验，未来的工作将集中在应用图像管理（从像素中学习）。下图显示了 DQN 的体系结构，其中我们馈送游戏屏幕，Q 网络近似于该游戏状态下所有操作的 Q 值。此外，该动作的估计与讨论的DQN算法相同。

图3.从像素概念中学习

        其次，未来的工作将侧重于实施DQN的决斗。在这个新架构中，我们指定了新的优势函数，它指定代理执行操作 a 与其他操作相比有多好（优势可以是正数或负数）。

        决斗 DQN 的体系结构与上述 DQN 相同，不同之处在于

        末端的连接层分为两个流（见下图）。
        在具有一定数量的操作空间处于一种状态的环境中，大多数计算的操作不会对状态产生任何影响。此外，还会有许多具有冗余效果的操作。在这种情况下，新的决斗 DQN 将比 DQN 体系结构更精确地估计 Q 值。

一个流计算值函数，另一个流计算优势函数（以确定哪个操作优先于另一个操作）。

图4.决斗 DQN 的体系结构

        最后，我们可以考虑从人类偏好中学习（OpenAI和Deep Mind）。瘦新概念的主要思想是根据人类的反馈来学习代理。接收人类反馈的代理将尝试执行人类喜欢的操作并设置

        相应的奖励。人与代理的互动直接有助于克服与设计奖励函数和复杂目标函数相关的挑战。

在我的Github中找到这个项目的完整代码。