时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比
时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比
目录
-
- 时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比
-
- 效果一览
- 基本描述
- 程序设计
- 参考资料
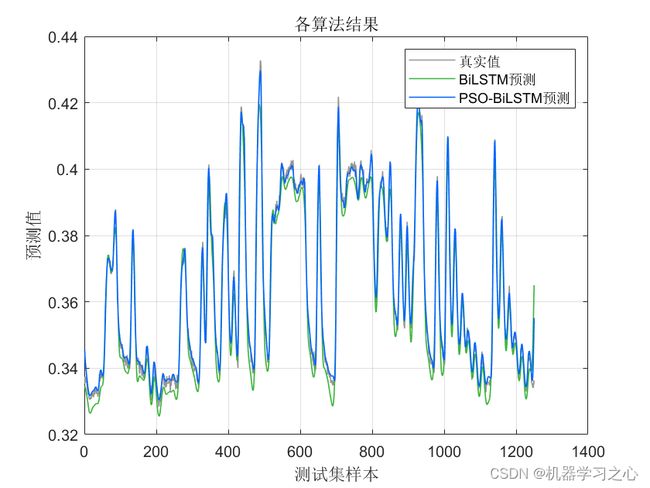
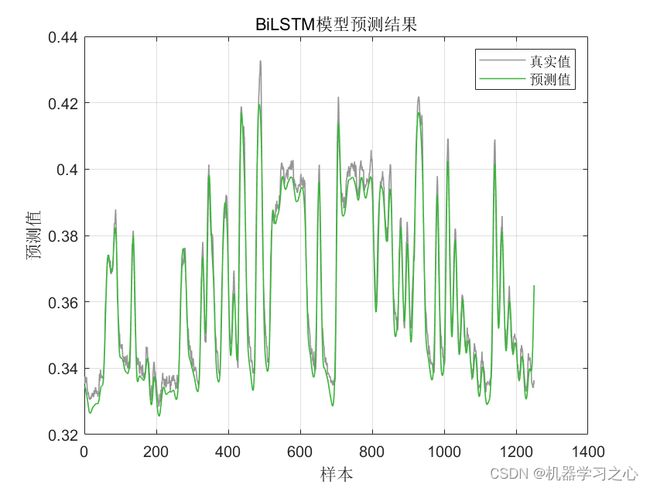
效果一览
基本描述
MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比。
1.Matlab实现PSO-BiLSTM和BiLSTM神经网络时间序列预测;
2.输入数据为单变量时间序列数据,即一维数据;
3.运行环境Matlab2020及以上,依次运行Main1BiLSTMTS、Main2PSOBiLSTMTS、Main3CDM即可,其余为函数文件无需运行,所有程序放在一个文件夹,data为数据集;
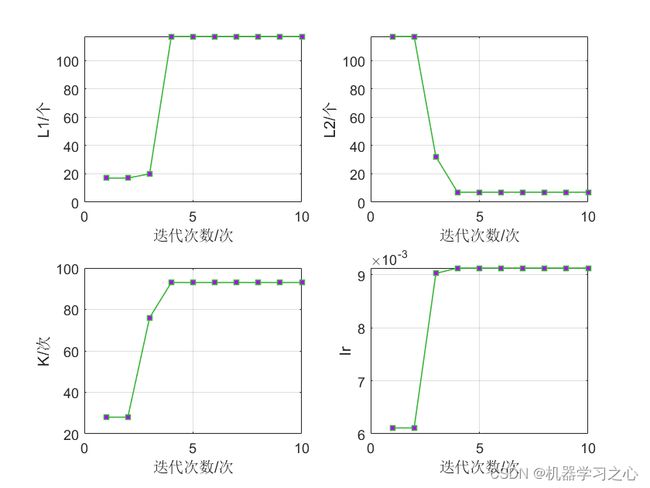
BiLSTM(双向长短时记忆模型)与粒子群算法优化后的BiLSTM(PSOBiLSTM)对比实验,可用于风电、光伏等负荷预测,时序预测,数据为单输入单输出,PSO优化超参数为隐含层1节点数、隐含层2节点数、最大迭代次数和学习率。
4.命令窗口输出MAE、MAPE、RMSE和R2;
程序设计
- 完整程序和数据下载:私信博主回复MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比。
for i=1:PopNum%随机初始化速度,随机初始化位置
for j=1:dim
if j==dim% % 隐含层节点与训练次数是整数 学习率是浮点型
pop(i,j)=(xmax(j)-xmin(j))*rand+xmin(j);
else
pop(i,j)=round((xmax(j)-xmin(j))*rand+xmin(j)); %
end
end
end
% calculate the fitness_value of Pop
pbest = pop;
gbest = zeros(1,dim);
data1 = zeros(Maxstep,PopNum,dim);
data2 = zeros(Maxstep,PopNum);
for i = 1:PopNum
fit(i) = fitness(pop(i,:),p_train,t_train,p_test,t_test);
f_pbest(i) = fit(i);
end
g = min(find(f_pbest == min(f_pbest(1:PopNum))));
gbest = pbest(g,:);
f_gbest = f_pbest(g);
%-------- in the loop -------------
for step = 1:Maxstep
mbest =sum(pbest(:))/PopNum;
% linear weigh factor
b = 1-step/Maxstep*0.5;
data1(step,:,:) = pop;
data2(step,:) = fit;
for i = 1:PopNum
a = rand(1,dim);
u = rand(1,dim);
p = a.*pbest(i,:)+(1-a).*gbest;
pop(i,:) = p + b*abs(mbest-pop(i,:)).*...
log(1./u).*(1-2*(u >= 0.5));
% boundary detection
for j=1:dim
if j ==dim
if pop(i,j)>xmax(j) | pop(i,j)<xmin(j)
pop(i,j)=(xmax(j)-xmin(j))*rand+xmin(j); %
end
else
pop(i,j)=round(pop(i,j));
if pop(i,j)>xmax(j) | pop(i,j)<xmin(j)
pop(i,j)=round((xmax(j)-xmin(j))*rand+xmin(j)); %
end
end
end
fit(i) = fitness(pop(i,:),p_train,t_train,p_test,t_test);
if fit(i) < f_pbest(i)
pbest(i,:) = pop(i,:);
f_pbest(i) = fit(i);
end
if f_pbest(i) < f_gbest
gbest = pbest(i,:);
f_gbest = f_pbest(i);
end
end
trace(step)=f_gbest;
step,f_gbest,gbest
result(step,:)=gbest;
end
or i=1:N%随机初始化速度,随机初始化位置
for j=1:D
if j==D% % 隐含层节点与训练次数是整数 学习率是浮点型
x(i,j)=(xmax(j)-xmin(j))*rand+xmin(j);
else
x(i,j)=round((xmax(j)-xmin(j))*rand+xmin(j)); %
end
end
v(i,:)=rand(1,D);
end
%------先计算各个粒子的适应度,并初始化Pi和Pg----------------------
for i=1:N
p(i)=fitness(x(i,:),p_train,t_train,p_test,t_test);
y(i,:)=x(i,:);
end
[fg,index]=min(p);
pg = x(index,:); %Pg为全局最优
%------进入主要循环,按照公式依次迭代------------
for t=1:M
for i=1:N
v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
for j=1:D
if j ~=D
x(i,j)=round(x(i,j));
end
if x(i,j)>xmax(j) | x(i,j)<xmin(j)
if j==D
x(i,j)=(xmax(j)-xmin(j))*rand+xmin(j); %
else
x(i,j)=round((xmax(j)-xmin(j))*rand+xmin(j)); %
end
end
end
temp=fitness(x(i,:),p_train,t_train,p_test,t_test);
if temp<p(i)
p(i)=temp;
y(i,:)=x(i,:);
end
if p(i)<fg
pg=y(i,:);
fg=p(i);
end
end
trace(t)=fg;
result(t,:)=pg;
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/127596777?spm=1001.2014.3001.5501
[2] https://download.csdn.net/download/kjm13182345320/86830096?spm=1001.2014.3001.5501