LeetCode第209次周赛
LeetCode第209次周赛
本次周赛题目都不算很难,但是有一种“剑走偏锋”的感觉。
No.1 特殊数组的特征值
给你一个非负整数数组 nums 。如果存在一个数 x ,使得 nums 中恰好有 x 个元素 大于或者等于 x ,那么就称 nums 是一个 特殊数组 ,而 x 是该数组的 特征值 。
注意: x 不必 是 nums 的中的元素。
如果数组 nums 是一个 特殊数组 ,请返回它的特征值 x 。否则,返回 -1 。可以证明的是,如果 nums 是特殊数组,那么其特征值 x 是 唯一的 。
示例 1:
输入:nums = [3,5]
输出:2
解释:有 2 个元素(3 和 5)大于或等于 2 。
示例 2:
输入:nums = [0,0]
输出:-1
解释:没有满足题目要求的特殊数组,故而也不存在特征值 x 。
如果 x = 0,应该有 0 个元素 >= x,但实际有 2 个。
如果 x = 1,应该有 1 个元素 >= x,但实际有 0 个。
如果 x = 2,应该有 2 个元素 >= x,但实际有 0 个。
x 不能取更大的值,因为 nums 中只有两个元素。
示例 3:
输入:nums = [0,4,3,0,4]
输出:3
解释:有 3 个元素大于或等于 3 。
示例 4:
输入:nums = [3,6,7,7,0]
输出:-1
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 1000
解析
本题是例行签到题。给定一个数组,要求我们找到一个整数x满足数组中大于等于x的数恰好有x个。由于本题数据范围很小,可以采用暴力枚举的方式求解。首先对数组排序,并获取数组最大值maxN与长度len,显然,如果存在这样的x,其范围一定在 0 − m i n ( m a x N , l e n ) 0 - min(maxN,len) 0−min(maxN,len)之间,因为数组里不存在超过最大值的数,数量也不可能多于元素总数量。因此,我们枚举所有可能的x,去计算数组大于等于x的元素的个数,看是否恰好等于x,如果是则找到所求直接返回即可(题目已经表示若存在就是唯一解),若范围呢所有数均不满足,则返回-1.
C++代码如下:
int specialArray(vector<int>& nums) {
sort(nums.begin(), nums.end());
int len = nums.size(),maxN = nums.back();
int up = min(len, maxN);
for (int i = 0; i <= up; ++i) {
int cur = nums.end() - (lower_bound(nums.begin(), nums.end(), i));
if (cur == i) return cur;
}
return -1;
}
排序复杂度 O ( N ∗ l o g N ) O(N*logN) O(N∗logN),枚举每个数再二分寻找大于等于它的数个数,复杂度也是 O ( N ∗ l o g N ) O(N*logN) O(N∗logN)。
No.2 奇偶树
如果一棵二叉树满足下述几个条件,则可以称为 奇偶树 :
二叉树根节点所在层下标为 0 ,根的子节点所在层下标为 1 ,根的孙节点所在层下标为 2 ,依此类推。
偶数下标 层上的所有节点的值都是 奇 整数,从左到右按顺序 严格递增
奇数下标 层上的所有节点的值都是 偶 整数,从左到右按顺序 严格递减
给你二叉树的根节点,如果二叉树为 奇偶树 ,则返回 true ,否则返回 false 。
示例 1:
输入:root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
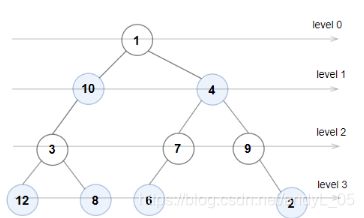
输出:true
解释:每一层的节点值分别是:
0 层:[1]
1 层:[10,4]
2 层:[3,7,9]
3 层:[12,8,6,2]
由于 0 层和 2 层上的节点值都是奇数且严格递增,而 1 层和 3 层上的节点值都是偶数且严格递减,因此这是一棵奇偶树。
输出:false
解释:每一层的节点值分别是:
0 层:[5]
1 层:[4,2]
2 层:[3,3,7]
2 层上的节点值不满足严格递增的条件,所以这不是一棵奇偶树。
示例 3:
输入:root = [5,9,1,3,5,7]
输出:false
解释:1 层上的节点值应为偶数。
解析
本题给定了合法奇偶树的标准:下标为偶数的那一层元素全是奇数且严格递增,下标为奇数的层全是偶数且严格递减。本题实际上就是加了一些判断的层序遍历,只要把每一层元素按照从左至右的顺序取出,同时知道这是第几层,根据标准去判断,符合就看下一层,不符合就直接返回false即可。
bool isEvenOddTree(TreeNode* root) {
int curL = 0;
queue<TreeNode*>qeven,qodd;
qeven.push(root);
while (!qodd.empty() || !qeven.empty()) {
if (!qeven.empty()) {
vector<int>check;
while (!qeven.empty()) {
TreeNode* cur = qeven.front();
qeven.pop();
check.push_back(cur->val);
if (cur->left) qodd.push(cur->left);
if (cur->right) qodd.push(cur->right);
}
int len = check.size();
for (auto c : check) {
if (c % 2 == 0) return false;
}
for (int i = 0; i < len - 1; ++i) {
if (check[i] >= check[i + 1]) return false;
}
}
else {
vector<int>check;
while (!qodd.empty()) {
TreeNode* cur = qodd.front();
qodd.pop();
check.push_back(cur->val);
if (cur->left) qeven.push(cur->left);
if (cur->right) qeven.push(cur->right);
}
int len = check.size();
for (auto c : check) {
if (c % 2 == 1) return false;
}
for (int i = 0; i < len - 1; ++i) {
if (check[i] <= check[i + 1]) return false;
}
}
}
return true;
}
维护两个队列,分别记录偶数层与奇数层的树节点,一层节点为偶数层那他们的子节点必然是在奇数层,反之亦然。首先偶数层放入根节点,在层序遍历结束前两个队列必然不都为空,每一层遍历结束会清空一个队列而填充另一个。每一层从左到右依次取出将数值记录在数组用于判断是否符合本层的规则,同时将其子节点加入另一个队列。直到两队列全空,遍历完成,此时若每一层都符合规则,那说明这棵树是题目规定的奇偶树,返回true;遍历过程中任何一层不满足,直接返回false。
注意题目要求是严格递增或递减,相邻元素相等也是不符合要求的。代码实际上可以继续优化。
No.3 可见点的最大数目
给你一个点数组 points 和一个表示角度的整数 angle ,你的位置是 location ,其中 location = [posx, posy] 且 points[i] = [xi, yi] 都表示 X-Y 平面上的整数坐标。
最开始,你面向东方进行观测。你 不能 进行移动改变位置,但可以通过 自转 调整观测角度。换句话说,posx 和 posy 不能改变。你的视野范围的角度用 angle 表示, 这决定了你观测任意方向时可以多宽。设 d 为逆时针旋转的度数,那么你的视野就是角度范围 [d - angle/2, d + angle/2] 所指示的那片区域。
对于每个点,如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ,那么你就可以看到它。
同一个坐标上可以有多个点。你所在的位置也可能存在一些点,但不管你的怎么旋转,总是可以看到这些点。同时,点不会阻碍你看到其他点。
返回你能看到的点的最大数目。
示例 1:
输入:points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
输出:3
解释:阴影区域代表你的视野。在你的视野中,所有的点都清晰可见,尽管 [2,2] 和 [3,3]在同一条直线上,你仍然可以看到 [3,3] 。

示例 2:
输入:points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
输出:4
解释:在你的视野中,所有的点都清晰可见,包括你所在位置的那个点。
解析
本题给定了一个位置和一群点,相当于我们在给定的location处以视角angle进行观察,可以确定一个视线范围,我们可以通过旋转来改变这个范围,求范围内能看到的最多的点的数量。
本题实际上是一个几何问题,我们是视线范围是从location出发的两条射线确定的区域,换言之,这两条射线分别确定了一个起始角度和一个终止角度,当一个点与location连线的角度在起始与终止角度之间,该点可以被观察到。
因此,本题可以转化为,已知一个角度范围,和每个点对应的角度值,求解当起始角度变化时,角度范围内包含的最多角度值的数量。我们将角度,定义为与x轴正方向的夹角,已知平面两个点,其连线与x轴正方向夹角的正切值,就是 ( y 1 − y 2 ) / ( x 1 − x 2 ) (y1-y2)/(x1-x2) (y1−y2)/(x1−x2),而求解角度,则需要反正切函数。在C++中,atan2(y, x)用于求解 a r c t a n y / x arctan y/x arctany/x的值,其返回值为弧度制,范围是(-PI,PI],其中逆时针方向从x轴正方向到负方向(x轴上方)的180度范围,取值是[0.PI],x轴下方的半圈是[0,-PI],其中x轴正方向为0,负方向为 ± P I \pm PI ±PI,显然,这里在X轴负方向存在突变点、不连续点,不利于我们后续寻找范围内的点数。
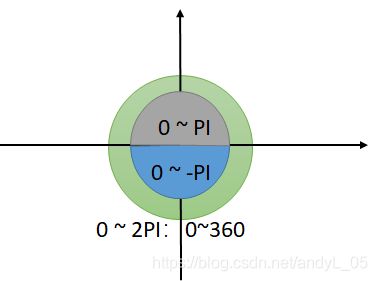
如上图所示,灰色与蓝色半圆分别是正负方向,取值不连续,我们通过转化将整个圆统一起来,也就是对于 α < 0 , α = 2 ∗ π + α \alpha<0,\alpha=2*\pi+\alpha α<0,α=2∗π+α将 [ − P I , 0 ] [-PI,0] [−PI,0]变为 [ P I , 2 ∗ P I ] [PI,2*PI] [PI,2∗PI],这样一圈的角度就如绿色圆所示,范围是 [ 0 , 2 ∗ P I ] [0,2*PI] [0,2∗PI]且连续了。
接下来,我们对每个点与location连线角度进行排序,从小到大的顺序,这样起始角度与终止角度之间的点数,就可以通过upper_bound这样的二分法求解。首先枚举一个角度,下标为i,作为start,加上angle角度就是终止角度end,那么通过upper_bound找到大于end的第一个点的下标j,在此之前到start的 j − i j-i j−i个点就是此时能观察到的点数。

由于角度是一个循环,360度就是0度,但是在数值上却无法直接找到。例如上图绿色的两条线,显然end(靠上方)的角度就是比start(靠下方)的要大,上述流程找到的 j − i j-i j−i即为所求。但如果是上图红色部分,观察区域跨过了x轴正方向,换言之, s t a r t < 360 , e n d > 360 start<360, end>360 start<360,end>360的情况,此时直接寻找无法找到全部观察点。举例,加入范围是330度到380度(20度),显然我们不存在超过360度的点,直接寻找比380大的,实际上只能返回这个数组最后一个(最大元素)后的位置,换句话说,只找到了330-360的点,毕竟20度在数值上就是不比360更大。这时候,我们就将观察区域分为两个部分,start到360 ,以及0到(end-360),也就是分别寻找x轴正半轴以下和以上的区域各有多少点,在加起来即可。
另外C++的反正切函数无法处理两个相同坐标点的正切值,因为y和x都是0,其结果是未定义的,所以计算角度时,如果目标点与观察点是同一个点,只要把它记下来,最后加上去即可,因为这个点无论怎样都看得到。
C++代码如下:
const double PI = 3.1415926535;
int visiblePoints(vector<vector<int>>& points, int angle, vector<int>& location) {
vector<double>ang;
int len = points.size(),same = 0;
for (int i = 0; i < len; ++i) {
if (points[i][1] - location[1] == 0 && points[i][0] - location[0] == 0) {
++same;
continue;
}
double a = atan2((double)(points[i][1] - location[1]), (double)(points[i][0] - location[0]));
cout << a << endl;
if (a < 0) a = 2 * PI + a;
a = a / PI * 180;
cout << a << endl;
ang.push_back(a);
}
int l = ang.size();
for (int i = 0; i < l; ++i) {
if (ang[i] >= 360) ang[i] -= 360;
}
sort(ang.begin(), ang.end());
int maxN = 0;
for (int i = 0; i < l; ++i) {
double start = ang[i];
double end = start + (double)angle;
int num = 0;
if (end < 360) {
num = (upper_bound(ang.begin(), ang.end(), end)) - (ang.begin() + i);
}
else {
num = l - i;
end = end - 360;
num+= (upper_bound(ang.begin(), ang.end(), end)) - (ang.begin());
}
maxN = max(maxN, num);
}
return maxN+same;
}
代码如上所示,ang数组记录所有的角度值,same则统计与观察点重合的点的数量。经过反正切求解的a,如果是负数,就变换到[PI,2*PI]之间。然后弧度转角度到[0, 360]之间的角度值,并排序。枚举每个角度作为start角度,叠加angle计算得到end,如果end<360表示没有跨过x轴正方向,直接计算点的数量;反之,就分为两段计算。每次枚举计算后更新点数的最大值。返回时记得把重合点same加上。
No.4 使整数变为 0 的最少操作次数
给你一个整数 n,你需要重复执行多次下述操作将其转换为 0 :
翻转 n 的二进制表示中最右侧位(第 0 位)。
如果第 (i-1) 位为 1 且从第 (i-2) 位到第 0 位都为 0,则翻转 n 的二进制表示中的第 i 位。
返回将 n 转换为 0 的最小操作次数。
示例 1:
输入:n = 0
输出:0
示例 2:
输入:n = 3
输出:2
解释:3 的二进制表示为 “11”
“11” -> “01” ,执行的是第 2 种操作,因为第 0 位为 1 。
“01” -> “00” ,执行的是第 1 种操作。
示例 3:
输入:n = 6
输出:4
解释:6 的二进制表示为 “110”.
“110” -> “010” ,执行的是第 2 种操作,因为第 1 位为 1 ,第 0 到 0 位为 0 。
“010” -> “011” ,执行的是第 1 种操作。
“011” -> “001” ,执行的是第 2 种操作,因为第 0 位为 1 。
“001” -> “000” ,执行的是第 1 种操作。
示例 4:
输入:n = 9
输出:14
示例 5:
输入:n = 333
输出:393
提示:
0 < = n < = 1 0 9 0 <= n <= 10^9 0<=n<=109
解析
本题看起来很复杂,是一系列的位操作,并且数据范围达到了 1 0 9 10^9 109,O(N)都会超时。直接求解的话,广度优先搜索,每次探索两种操作的一个,直到得到0.可以在求解中保存计算过的数及其操作数,以便查表避免重复计算,但依然觉得较为复杂。
我一开始认为此题有数学解(确实有),然后开始找规律,最初认为,要想变为0,需要
先把二进制每一位变换为1,再从全1变为0,而后者基于1的个数存在一定的规律,但是没写出来。
比赛结束后,观察了一下这个操作,以及每个数需要的操作数,可以发现:
| 数字 | 操作数 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 3 |
| 3 | 2 |
| 4 | 7 |
| 5 | 6 |
| 6 | 4 |
| 7 | 5 |
| 8 | 15 |
| 9 | 14 |
根据题设的操作,无论是哪一种操作,要么是最后一位变化,要么是满足题设的第i为变化,每次只变化一位,听起来有点像格雷码的操作。
在查询一下格雷码编码的二进制数,在十进制下的表示顺序:
0,1,3,2,6,7,5,4,12,13,15,14,10,11,9,8…
可发现,实际上题目要求的就是格雷码索引值。题目的最优操作,就是逆向递推格雷码的过程,
比如3-1-0,实际上就是反向、不断求前一个格雷码直到0,那操作数,自然就是这个数格雷码的索引值(第几个格雷码,自然需要递推几次),因此本题就是格雷码转化2进制即可。(所谓的格雷码与二进制转化,就是把第n个自然顺序数,与第n个格雷码数对应起来相互转化的方法,而从0开始(下标也从0开始)的自然顺序数,数值与索引就是一个值)
C++代码如下:
int minimumOneBitOperations(int n) {
int y = n;
while (n >>= 1)
y ^= n;
return y;
}
