卷积计算代码实现

问题

写代码实现卷积操作

问题解答

有两种方式实现，一种是通过滑动窗口的方式，一种是通过转化为矩阵乘法的方式， 后者比前者执行速度快许多

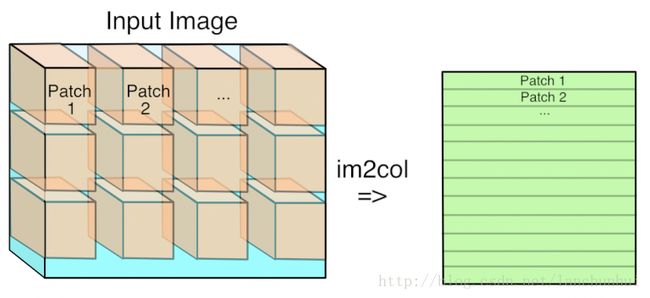
将卷积运算转化为矩阵乘法，从乘法和加法的运算次数上看，两者没什么差别，但是转化成矩阵后，运算时需要的数据被存在连续的内存上，这样访问速度大大提升（cache），同时，矩阵乘法有很多库提供了高效的实现方法，像BLAS、MKL等，转化成矩阵运算后可以通过这些库进行加速。

缺点呢？这是一种空间换时间的方法，消耗了更多的内存——转化的过程中数据被冗余存储。

还有两张形象化的图片帮助理解：

代码实现

# 简化计算，假设batchsize为1， 卷积核个数为1
import numpy as np
# 滑窗实现
class Conv2d(object):
    def __init__(self, img, c_out, kernel, stride, padding):
        self.img = img
        self.c_out = c_out
        self.kernel = kernel
        self.stride = stride
        self.padding = padding

    def conv(self):
        input_c, input_h, input_w = self.img.shape
        # out_ = []
        # for c_o in range(self.c_out):
        output = []
        #分通道划窗计算
        for c in range(input_c):
            out = self.compute_conv(input[c], self.kernel[c])
            output.append(out)
            # out_.append(sum(output))
        return sum(output)

    def compute_conv(self, input_c, kernel_c):
        k, _ = kernel_c.shape
        h, w = input_c.shape

        if self.padding == "valid":
            out_h = (h - k)//self.stride + 1
            out_w = (w - k)//self.stride + 1
            pad_h, pad_w = 0, 0

        if self.padding == "same":
            out_h, out_w = h, w
            pad_w = (w*(self.stride-1)+k-self.stride)//2
            pad_h = (h*(self.stride-1)+k-self.stride)//2

        if self.padding == "full":
            pad_w = k-1
            pad_h = k-1
            out_h = (w + 2*pad_h - k) // self.stride + 1
            out_w = (h + 2*pad_w - k) // self.stride + 1
        input_padding = np.zeros((h+pad_h*2, w+pad_w*2))
        input_padding[pad_h:pad_h+h, pad_w:pad_w+w] = input_c
        out = np.zeros((out_h, out_w))
        for i in range(0, out_h):
            for j in range(0, out_w):
                out[i, j] = np.sum(input_padding[i*self.stride:i*self.stride+k, j*self.stride:j*self.stride+k] * kernel_c)
        return out

# 矩阵实现
class Conv2dMatrix():
    def __init__(self, img, c_out, kernel, stride, padding):
        self.img = img
        self.c_out = c_out
        self.kernel = kernel
        self.stride = stride
        self.padding = padding

    def conv(self):
        c, h, w = self.img.shape
        c_k, k, _ = self.kernel.shape
        if self.padding == "same":
            out_h, out_w = h, w
            pad_w = (self.stride*(w-1) - w + k) // 2
            pad_h = (self.stride*(h-1) - h + k) // 2
        if self.padding == "valid":
            out_h = (h-k) // self.stride + 1
            out_w = (w-k) // self.stride + 1
            pad_h = 0
            pad_w = 0
        if self.padding == "full":
            pad_w = k - 1
            pad_h = k - 1
            out_h = (h + 2*pad_h - k) // self.stride + 1
            out_w = (w + 2*pad_w - k) // self.stride + 1
        img_padding = np.zeros((c, h+2*pad_h, w+2*pad_w))
        img_padding[:, pad_h:pad_h+h, pad_w:pad_w+w] = self.img
        feature_matrix = np.zeros((out_w*out_h, c_k*k*k))
        patch = 0
        for i in range(out_h):
            for j in range(out_w):
                feature_patch = img_padding[:, i*self.stride:i*self.stride+k, j*self.stride:j*self.stride+k]
                feature_matrix[patch] = feature_patch.flatten()
                patch += 1
        kernel_matrix = self.kernel.reshape(c_k*k*k, 1)
        return np.dot(feature_matrix, kernel_matrix).reshape(out_h, out_w)


input = np.array([[[1, 2, 3, 4, 5, 6, 7]]*7]*3)
input = input.reshape(-1, input.shape[1], input.shape[2])
kernel = np.array([[[0, 1, 1], [1, 0, 1], [1, 0, 0]]]*3)
kernel = kernel.reshape(-1, kernel.shape[1], kernel.shape[2])
conv2d = Conv2d(input, 1, kernel, 1, padding="full")
out = conv2d.conv()
print(out)

conv2d_m = Conv2dMatrix(input, 1, kernel, 1, padding='full')
out = conv2d_m.conv()
print(out)

参考资料

１、im2col：将卷积运算转为矩阵相乘
２、面试基础–深度学习　卷积及其代码实现
3、 卷积前向计算代码实现