动态规划问题(最大子段和问题),分治法问题(二路归并算法),贪心算法问题(实现钱币问题),回溯法问题(n皇后问题)
就这!!就这!!就这!!哈哈哈哈。
(一)就自己对与这几个算法的一些总结。
1.动态规划法: 基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解,以自底向上的方式解各子问题。
2.分治法问题: 将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
注: 你会发现,其实这两个没啥区别,都是大问题分解成小问题,然后找最优解的问题。不同的是分治法分解后的子问题是相互独立的,不相同。而动态规划法分解后的子问题有相同的,保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。
3.贪心算法问题: 采用自顶向下,以迭代的方法做出相继的贪心选择,每做一次贪心选择,就将所求问题简化为一个规模更小的子问题,通过每一步贪心选择,可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解,但由此产生的全局解有时不一定是最优的。
4.回溯法问题: 一般都是问题的解空间转化成了图或者树的结构表示,然后使用深度优先搜索策略进行遍历,遍历的过程中记录和寻找所有可行解或者最优解。
(二)各个方法的详解
1.动态规划法:
(1)在解决动态规划问题时一般分为四步:
1、定义一个状态,这是一个最优解的结构特征
2、进行状态递推,得到递推公式
3、进行初始化
4、返回结果
(2)适用性
1、最优子结构性质
2、无后效性
3、子问题的重叠性
2.分治法:
(1)在每一层的递归上的步骤
1、分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题。
2、解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题。
3、合并:将各个子问题的解合并为原问题的解。
它的一般的算法设计模式如下:
Divide-and-Conquer(P)
1. if |P|≤n0
2. then return(ADHOC(P))
3. 将P分解为较小的子问题 P1 ,P2 ,...,Pk
4. for i←1 to k
5. do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi
6. T ← MERGE(y1,y2,...,yk) △ 合并子问题
7. return(T)
其中|P|表示问题P的规模;n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。
ADHOC(P)是该分治法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过n0时直接用算法
ADHOC(P)求解。算法MERGE(y1,y2,...,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,...,Pk的相应的解
y1,y2,...,yk合并为P的解。
(2)适用性
1、该问题的规模缩小到一定的程度就可以容易地解决。
2、该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
3、利用该问题分解出的子问题的解可以合并为该问题的解。
4、该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
3.贪心算法:
(1)算法的步骤
1、建立数学模型来描述问题。
2、把求解的问题分成若干个子问题。
3、对每个子问题求解,得到子问题的局部最优解。
4、把子问题的解局部最优解合成原来解问题的一个解。
(2)适用性(基本要素)
1、贪心选择性质
2、最优子结构性质
该算法存在问题:
1. 不能保证求得的最后解是最佳的;
2. 不能用来求最大或最小解问题;
3. 只能求满足某些约束条件的可行解的范围。
4.回溯法问题:
(1)关键要素
1、针对给定的问题,定义问题的解空间。
2、确定易于搜索的解空间结构。
3、以深度优先方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。
(1)有两种实现回溯法(递归法和迭代法)
1、递归:
函数模板如下:
void BackTrace(int t) {
if(t>n)
Output(x);
else
for(int i = f (n, t); i <= g (n, t); i++ ) {
x[t] = h(i);
if(Constraint(t) && Bound (t))
BackTrace(t+1);
}
}
2、迭代:
函数模板如下:
void IterativeBackTrace(void) {
int t = 1;
while(t>0) {
if(f(n, t) <= g( n, t))
for(int i = f(n, t); i <= g(n, t); i++ ) {
x[t] = h(i);
if(Constraint(t) && Bound(t)) {
if ( Solution(t))
Output(x);
else
t++;
}
}
else
t− −;
}
}
(三)各个算法的具体例子
1.动态规划
使用动态规划法解决最大子段和问题:
题目: 给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和,全为负数时,返回0。
思路方法: 用一个MaxSum来保存前面得到的子串的数值,当遍历到array[i]且MaxSum<0的时候,前面的子串对当前的加和是没有贡献的,所以舍弃掉这样的子串,让MaxSum =array[i],重新开始子串的累积,而如果MaxSum>0,那么前面的子串对加和是有贡献的,所以继续追加子串,MaxSum= array[i] + MaxSum;这样每次循环还检验更新最大值就可以了。
空间复杂度O(1).
下面为实现的代码:
#include
using namespace std;
int min,max; //最大子段和区间
//动态规划法
int MaxSubSum3(int array[],int n){
int MaxSum=0;
int t=0;
for(int i=0;iarray[i]) {
t=t+array[i];
}else{
t=array[i]; //重新记录起点
}
//记录字段和的下标
if(t==array[i]){ //新的起点
min=i;
}else{
max=i; //终点
}
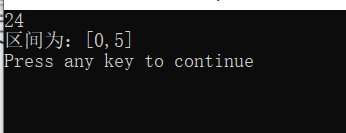
if(MaxSum 2.分治法问题
使用分治法来实现二路归并算法:
题目: 二路归并算法
思路方法:
将目标数组a[ ]分成左右两个数组,然后用两个指针分别记录左右两个数组,一一比较放入temp[ ]数组中。如果发现左边数组没排完,就加入到temp[ ]中,右边同理。再将数组赋值到目标数组a[ ]。
使用递归来实现二路归并排序。
下面为实现代码:
//归并排序
#include
using namespace std;
//将数组a[left,mid]与数组a[mid,right]合并
void MergeArr(int a[],int left,int mid,int right,int temp[]){
int k=0,rmid=mid+1;
int i=left,j=right; //i和j来指向左右两个数组操作
while(i<=mid && rmid<=j){
if(a[i] <= a[rmid]){
temp[k++]=a[i++];
}else{
temp[k++]=a[rmid++];
}
}
while(i <= mid){
temp[k++] = a[i++];
}
while(rmid <= j){
temp[k++] = a[rmid++];
}
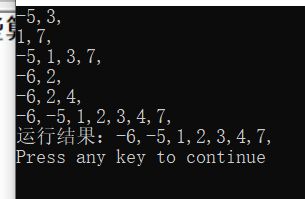
for(i=0;i 运行结果:
注: 最后一行为运行结果,前面几行都是他的二路归并过程。
3.贪心算法
使用贪心算法实现钱币问题
题目: 指定币值和相应的数量,用最少的数量凑齐某金额。
思路方法: 我们就直接优先选择面值大的钱币,以此类推,直到凑齐总金额。(贪心不一定最优)
下面为实现代码:
//题目: 指定币值和相应的数量,用最少的数量凑齐某金额。
#include
using namespace std;
int main(){
int money[] = { 1, 2, 5, 10, 20, 50, 100 };//拥有的面额
int counts[] = { 3, 3, 2, 1, 1, 3, 3 }; //所对应面额的张数
int sum=246; //所需要换的钱数;
int result[7];
int add=0; //当前凑的金额
for(int i=6;i>=0;i--)
{
int num = ((sum-add)/money[i]);
if(num>counts[i])
{
num=counts[i];
}
add=add+num*money[i];
result[i]=num;
}
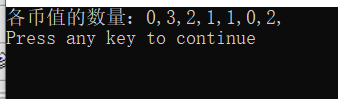
cout<<"各币值的数量:";
for(int j=0;j<7;j++){
cout< 4.回溯法问题
使用回溯法解决n皇后问题
题目: 在n×n格的国际象棋上摆放n个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
思路方法: 使用回溯法,放一个皇后,判断他的八个方向是否有皇后,用数组来存储。
下面是实现代码:
#include
using namespace std;
int count = 0; //摆法个数
const int nqueen=8;//设置皇后的个数
//判断当前位置是否能放皇后
bool IsSet(int i, int j, int (*Q)[nqueen])
{
int s,t;
//判断某一行上是否能放皇后
for(s=i,t=0;t=0&&t>=0;s--,t--){
if(Q[s][t]==1)
return false;
}
//判断右下是否能放皇后
for(s=i+1,t=j+1;s=0&&t=0;s++,t--){
if(Q[s][t]==1)
return false;
}
//其它情况
return true;
}
//放置皇后
void Queen(int j, int (*Q)[nqueen])
{
int i,k;
if(j==nqueen) //如果8个皇后全部放置完毕
{
for(i=0;i