Leetcode刷题笔记——剑指 Offer 60. n个骰子的点数(中等)
文章目录
- 题目描述
- 解法
-
- 复杂度分析
- C++代码实现
- 参考链接
题目描述
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
示例 1:
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
解法
设输入 n n n 个骰子的解(即概率列表)为 f ( n ) f(n) f(n) ,其中「点数和」 x x x 的概率为 f ( n , x ) f(n,x) f(n,x) 。
假设已知 n − 1 n−1 n−1 个骰子的解 f ( n − 1 ) f(n - 1) f(n−1) ,此时添加一枚骰子,求 n n n 个骰子的点数和为 x x x 的概率 f ( n , x ) f(n,x) f(n,x) 。
当添加骰子的点数为 1 1 1 时,前 n − 1 n - 1 n−1 个骰子的点数和应为 x − 1 x - 1 x−1 ,方可组成点数和 x x x ;同理,当此骰子为 2 2 2 时,前 n − 1 n - 1 n−1 个骰子应为 x − 2 x - 2 x−2 ;以此类推,直至此骰子点数为 6 6 6 。将这 6 6 6 种情况的概率相加,即可得到概率 f ( n , x ) f(n, x) f(n,x) 。递推公式如下所示:
f ( n , x ) = ∑ i = 1 6 f ( n − 1 , x − i ) × 1 6 f(n,x)=\sum^{6}_{i=1}f(n−1,x−i)×\frac{1}{6} f(n,x)=i=1∑6f(n−1,x−i)×61根据以上分析,得知通过子问题的解 f ( n − 1 ) f(n - 1) f(n−1) 可递推计算出 f ( n ) f(n) f(n) ,而输入一个骰子的解 f ( 1 ) f(1) f(1) 已知,因此可通过解 f ( 1 ) f(1) f(1) 依次递推出任意解 f ( n ) f(n) f(n) 。
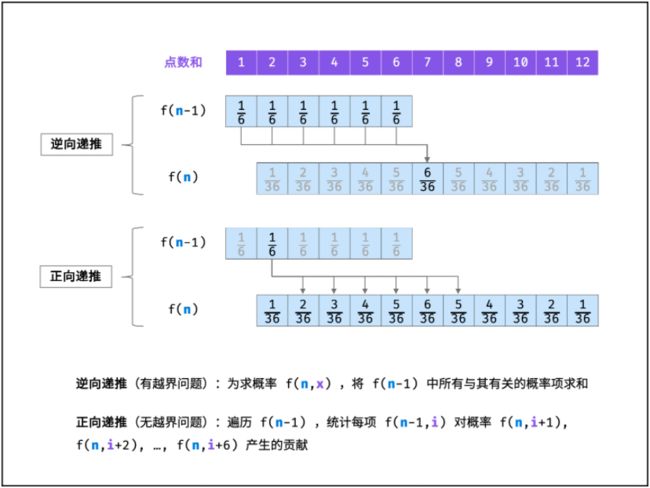
如下图所示,为 n = 2 n = 2 n=2 , x = 7 x = 7 x=7 的递推计算示例。

观察发现,以上递推公式虽然可行,但 f ( n − 1 , x − i ) f(n-1, x-i) f(n−1,x−i) 中的 x − i x - i x−i 会有越界问题。例如,若希望递推计算 f ( 2 , 2 ) f(2, 2) f(2,2),由于一个骰子的点数和范围为 [ 1 , 6 ] [1, 6] [1,6] ,因此只应求和 f ( 1 , 1 ) f(1, 1) f(1,1) ,即 f ( 1 , 0 ) , f ( 1 , − 1 ) , . . . , f ( 1 , − 4 ) f(1, 0) , f(1, -1) , ... , f(1, -4) f(1,0),f(1,−1),...,f(1,−4) 皆无意义。此越界问题导致代码编写的难度提升。
如下图所示,以上递推公式是 “逆向” 的,即为了计算 f ( n , x ) f(n, x) f(n,x) ,将所有与之有关的情况求和;而倘若改换为 “正向” 的递推公式,便可解决越界问题。
具体来看,由于新增骰子的点数只可能为 1 1 1 至 6 6 6 ,因此概率 f ( n − 1 , x ) f(n - 1, x) f(n−1,x) 仅与 f ( n , x + 1 ) , f ( n , x + 2 ) , . . . , f ( n , x + 6 ) f(n, x + 1) , f(n, x + 2), ... , f(n, x + 6) f(n,x+1),f(n,x+2),...,f(n,x+6) 相关。因而,遍历 f ( n − 1 ) f(n - 1) f(n−1) 中各点数和的概率,并将其相加至 f ( n ) f(n) f(n) 中所有相关项,即可完成 f ( n − 1 ) f(n - 1) f(n−1) 至 f ( n ) f(n) f(n) 的递推。
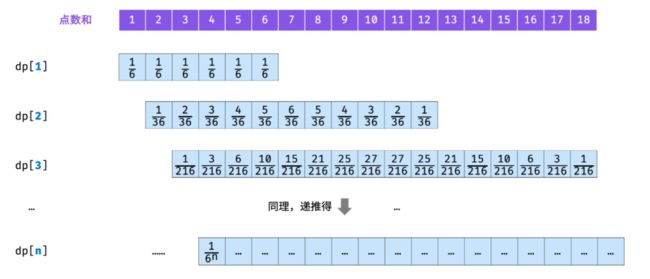
将 f ( i ) f(i) f(i) 记为动态规划列表形式 d p [ i ] dp[i] dp[i] ,则 i = 1 , 2 , . . . , n i = 1, 2, ..., n i=1,2,...,n 的状态转移过程如下图所示。
复杂度分析
- 时间复杂度 O ( n 2 ) O(n ^ 2) O(n2) : 状态转移循环 n − 1 n - 1 n−1 轮;每轮中,当 i = 2 , 3 , . . . , n i = 2, 3, ..., n i=2,3,...,n 时,对应循环数量分别为 6 × 6 , 11 × 6 , . . . , [ 5 ( n − 1 ) + 1 ] × 6 6 \times 6, 11 \times 6, ..., [5(n - 1) + 1] \times 6 6×6,11×6,...,[5(n−1)+1]×6 ;因此总体复杂度为 O ( ( n − 1 ) × 6 + [ 5 ( n − 1 ) + 1 ] 2 × 6 ) O((n - 1) \times \frac{6 + [5(n - 1) + 1]}{2} \times 6) O((n−1)×26+[5(n−1)+1]×6) ,即等价于 O ( n 2 ) O(n^2) O(n2) 。
- 空间复杂度 O ( n ) O(n) O(n) : 状态转移过程中,辅助数组 tmp 最大长度为 6 ( n − 1 ) − [ ( n − 1 ) − 1 ] = 5 n − 4 6(n-1) - [(n-1) - 1] = 5n - 4 6(n−1)−[(n−1)−1]=5n−4 ,因此使用 O ( 5 n − 4 ) = O ( n ) O(5n - 4) = O(n) O(5n−4)=O(n) 大小的额外空间。
C++代码实现
class Solution {
public:
vector<double> dicesProbability(int n) {
vector<double> dp(6, 1.0 / 6.0);
for (int i = 2; i <= n; i++) {
vector<double> tmp(5 * i + 1, 0);
for (int j = 0; j < dp.size(); j++) {
for (int k = 0; k < 6; k++) {
tmp[j + k] += dp[j] / 6.0;
}
}
dp = tmp;
}
return dp;
}
};
参考链接
[1] https://leetcode-cn.com/problems/nge-tou-zi-de-dian-shu-lcof/solution/jian-zhi-offer-60-n-ge-tou-zi-de-dian-sh-z36d/