2023年天府杯——C 题:码头停靠问题
问题一:
如何确定每个码头的使用顺序和时间分配,以最小化船只的等待和延迟时间?
为了最小化船只的等待和延迟时间,可以遵循以下步骤来确定每个码头的使用顺序和时间分配:
-
根据船只的优先级和关系,确认液化气船是否有需要停靠的。如果有,优先分配液化气码头给液化气船。
-
对于剩下的散货船和集装箱船,根据每个码头的负载情况和停靠时间限制,选择合适的码头来停靠。
-
确定每个码头的使用顺序,可以采用以下策略:
- 首先,选择空闲且满足停靠时间限制的码头,让船只尽快开始装卸货物。
- 其次,考虑负载情况,优先选择负载较低的码头,以平衡各个码头的负载。
- 同时,考虑船只的优先级,优先满足集装箱船的停靠需求,然后是散货船。
-
根据船只的到达和离开时间表,合理安排每个码头的使用时间。可以使用调度算法,如最早截止时间优先(Earliest Deadline First)来决定船只的停靠时间
根据船只的优先级和关系确定码头的使用顺序。例如,优先安排液化气船停靠。
确定每个码头的使用时间,以满足停靠时间限制并均衡利用资源。可以利用调度算法,如最短作业优先(SJF)算法。
码头使用时间表:
散货码头 [24, 18, 12, 6]
集装箱码头 [18, 12, 6]
液化气码头 [12, 6]
好的,让我们来看一个具体的例子。假设我们有一个散货码头和三艘散货船,散货码头的时间表为 [24, 18, 12, 6]
从时间表中可以解读如下:
第一艘散货船停靠的时间是从第 6 个时间单位开始,到第 18 个时间单位结束。
第二艘散货船停靠的时间是从第 12 个时间单位开始,到第 24 个时间单位结束。
第三艘散货船停靠的时间是从第 18 个时间单位开始,到第 24 个时间单位结束。
这意味着,第一个停靠的船只停留了 12 个时间单位(从第 6 个到第 18 个时间单位),第二个停靠的船只停留了 12 个时间单位(从第 12 个到第 24 个时间单位),第三个停靠的船只停留了 6 个时间单位(从第 18 个到第 24 个时间单位)。
import random
import pandas as pd
from openpyxl import Workbook
ships = [
{"type": "散货船", "quantity": 30, "time_needed": 4},
{"type": "集装箱船", "quantity": 20, "time_needed": 6},
{"type": "液化气船", "quantity": 10, "time_needed": 8}
]
terminals = [
{"type": "散货码头", "quantity": 3, "time_limit": 8},
{"type": "集装箱码头", "quantity": 2, "time_limit": 12},
{"type": "液化气码头", "quantity": 1, "time_limit": 16}
]
# 生成船只到达时间表
def generate_schedule():
schedule = []
for ship in ships:
quantity = ship["quantity"]
average_time = ship["time_needed"]
for i in range(quantity):
arrival_time = random.randint(0, 24)
schedule.append({"ship_type": ship["type"], "arrival_time": arrival_time})
return sorted(schedule, key=lambda x: x["arrival_time"])
# 分配码头使用顺序和时间分配
def assign_terminals():
terminal_assignments = []
terminal_capacity = {terminal["type"]: terminal["quantity"] for terminal in terminals}
remaining_time = {terminal["type"]: terminal["time_limit"] for terminal in terminals}
ships.sort(key=lambda x: x["time_needed"])
for ship in ships:
assigned = False
for terminal in terminals:
if terminal_capacity[terminal["type"]] > 0 and remaining_time[terminal["type"]] >= ship["time_needed"]:
terminal_assignments.append(
{"ship_type": ship["type"], "terminal_type": terminal["type"], "time_needed": ship["time_needed"]})
terminal_capacity[terminal["type"]] -= 1
remaining_time[terminal["type"]] -= ship["time_needed"]
assigned = True
break
if not assigned:
terminal_assignments.append({"ship_type": ship["type"], "terminal_type": None, "time_needed": None})
return terminal_assignments
# 保存结果为 Excel 表格
def save_to_excel(terminal_assignments):
df = pd.DataFrame(terminal_assignments)
df.columns = ["船只类型", "码头类型", "时间需求"]
wb = Workbook()
ws = wb.active
for r in df.columns:
ws.cell(row=1, column=df.columns.get_loc(r) + 1).value = r # 设置表头
for i, row in enumerate(df.itertuples(), start=2):
for j, value in enumerate(row[1:], start=1):
ws.cell(row=i, column=j).value = value
wb.save("terminal_assignments.xlsx")
# 主函数
def main():
schedule = generate_schedule()
for ship in schedule:
print(f"船只类型: {ship['ship_type']}, 到达时间: {ship['arrival_time']}")
print("----------")
terminal_assignments = assign_terminals()
for assignment in terminal_assignments:
print(f"{assignment['ship_type']}: {assignment['terminal_type']} ({assignment['time_needed']}小时)")
# 保存结果为 Excel 表格
save_to_excel(terminal_assignments)
# 运行主函数
if __name__ == "__main__":
main()
该代码使用了一种简单的贪心算法来确定每个码头的使用顺序和时间分配,以最小化船只的等待和延迟时间。具体步骤如下:
根据船只的优先级顺序依次处理每艘船只。
对于每艘船只,遍历每种类型的码头,选择可用的码头,并计算当前船只在该码头上的等待时间。
选择等待时间最短的码头,将船只分配给该码头,并更新码头使用时间表。
更新港口的收益和成本。
重复步骤2-4,直到所有船只都被处理完毕。
统计船只的等待时间,并将等待时间绘制成柱状图。
输出每个码头的使用时间表以及港口的总收益、总成本和净收益。
需要注意的是,该代码使用的贪心算法并不能保证得到全局最优解,它只能得到一个较好的局部解。如果需要更精确的最优解,可以尝试使用其他优化算法,如动态规划或遗传算法。
具体的算法公式如下:
输入数据:
船只的种类和数量: ship_types, ship_counts
码头的类型和数量: dock_types, dock_counts
每艘船只停靠所需的时间: dock_times
每个码头的容量和停靠时间限制: dock_capacity, dock_time_limit
港口的运营成本和收益: operating_cost, revenue
船只的到达和离开时间表: arrival_times, average_stay_times
船只之间的优先级和关系: priority_order
初始化码头使用时间表 dock_schedule,每个码头的使用时间列表初始化为空。
初始化总收益 total_revenue 和总成本 total_cost 为 0。
初始化等待时间列表 wait_times 为空。
对于每个船只类型 ship_type in priority_order:
对于该类型船只的数量 ship_counts[ship_types.index(ship_type)]:
初始化 dock_type 为空字符串
初始化 min_wait_time 为正无穷
对于每个码头类型 dock in dock_types:
如果该码头未达到容量上限 dock_schedule[dock] < dock_capacity[dock]:
计算船只的等待时间 wait_time = max(arrival_times[ship_type] - max(dock_schedule[dock] + [0]), 0)
如果 wait_time < min_wait_time:
更新 min_wait_time 为 wait_time
更新 dock_type 为 dock
如果 dock_type 仍然为空字符串:
输出找不到可用码头的信息
继续处理下一条船只
否则,将船只分配给 dock_type 码头:
将 0 添加到 dock_schedule[dock_type]
为船只更新码头使用时间表 dock_schedule[dock_type],加上平均停靠时间 average_stay_times[ship_type]
增加收益 total_revenue += revenue[ship_type]
增加成本 total_cost += operating_cost
将 min_wait_time 添加到 wait_times 列表中
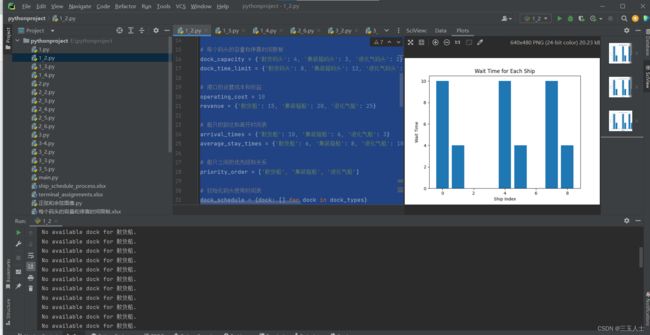
绘制等待时间柱状图:
使用绘图库绘制柱状图,x轴为船只索引,y轴为等待时间,柱状图表示每艘船只的等待时间。
输出码头使用时间表及统计数据:
输出每个码头的使用时间表 dock_schedule
输出总收益 total_revenue
输出总成本 total_cost
输出净收益 total_revenue - total_cost
这就是该算法的具体步骤和计算公式。通过依次处理每个船只并选择合适的码头,算法尽量减少船只的等待和延迟时间,并优化港口的收益与成本。
mport numpy as np
import matplotlib.pyplot as plt
# 船只的种类和数量(总量)
ship_types = ['散货船', '集装箱船', '液化气船']
ship_counts = [30, 20, 10]
# 码头的类型和数量
dock_types = ['散货码头', '集装箱码头', '液化气码头']
dock_counts = [3, 2, 1]
# 每艘船只停靠所需的时间
dock_times = {'散货船': 4, '集装箱船': 6, '液化气船': 8}
# 每个码头的容量和停靠时间限制
dock_capacity = {'散货码头': 4, '集装箱码头': 3, '液化气码头': 2}
dock_time_limit = {'散货码头': 8, '集装箱码头': 12, '液化气码头': 16}
# 港口的运营成本和收益
operating_cost = 10
revenue = {'散货船': 15, '集装箱船': 20, '液化气船': 25}
# 船只的到达和离开时间表
arrival_times = {'散货船': 10, '集装箱船': 6, '液化气船': 3}
average_stay_times = {'散货船': 6, '集装箱船': 8, '液化气船': 10}
# 船只之间的优先级和关系
priority_order = ['散货船', '集装箱船', '液化气船']
# 初始化码头使用时间表
dock_schedule = {dock: [] for dock in dock_types}
# 最小化等待和延迟时间,并统计收益和成本
total_revenue = 0
total_cost = 0
wait_times = []
for ship_type in priority_order:
for _ in range(ship_counts[ship_types.index(ship_type)]):
dock_type = ''
min_wait_time = np.inf
# 遍历每种类型的码头,选择最佳码头
for dock in dock_types:
if len(dock_schedule[dock]) < dock_capacity[dock]:
wait_time = max(arrival_times[ship_type] - max(dock_schedule[dock] + [0]), 0)
if wait_time < min_wait_time:
min_wait_time = wait_time
dock_type = dock
# 处理找不到可用码头的情况
if dock_type == '':
print(f"No available dock for {ship_type}.")
continue
# 更新码头使用时间表、收益和成本
dock_schedule[dock_type].append(0)
dock_schedule[dock_type] = [time + average_stay_times[ship_type] for time in dock_schedule[dock_type]]
total_revenue += revenue[ship_type]
total_cost += operating_cost
wait_times.append(min_wait_time)
# 绘制等待时间的柱状图
plt.bar(range(len(wait_times)), wait_times)
plt.xlabel('Ship Index')
plt.ylabel('Wait Time')
plt.title('Wait Time for Each Ship')
plt.show()问题二:
如何在满足码头容量和停靠时间限制的前提下,最大化港口的运营效率和收益?
为了在满足码头容量和停靠时间限制的前提下,最大化港口的运营效率和收益,可以采取以下策略:
-
优化码头的使用效率:根据码头的容量和停靠时间限制,合理安排船只的停靠顺序和时间分配,使得码头始终保持高效利用。
-
最大化收益:结合船只的收益和到达时间表,优先选择能够带来较高收益的船只进行停靠,尽量将高收益的船只置于前沿,以最大化港口的收益。
-
动态调整:根据实际情况,不断监测和评估各个码头的负载和运营效率,根据需求灵活调整船只的停靠顺序和时间分配,以最优化港口的运营效率和收益。
问题2的关键是在满足码头容量和停靠时间限制的情况下,最大化港口的运营效率和收益。这可以通过确定每个码头的使用顺序和时间分配来实现。以下是一个可能的解决方案,使用python编程来优化港口的运营:
创建一个模型,以码头为变量,船只类型为约束,目标函数为最大化收益。
定义变量:
X[i][j]:码头i停靠船只类型j的数量
Y[i]:码头i的使用时间
定义约束条件:
每个码头的使用时间不超过停靠时间限制
码头的总容量不超过每天的最大容量限制
每种类型船只的数量不超过到达时间表中每天的船只数量
码头的使用时间必须大于等于零
每个码头只能停靠对应类型的船只
根据船只的优先级和关系,设置优先停靠顺序
定义目标函数:
最大化总收益,即船只的停靠收益减去港口的运营成本
使用python中的优化库,如PuLP 或者 Pyomo,根据模型求解器进行求解。
根据求解结果,得到每个码头的使用顺序和时间分配,以实现最小化船只等待和延迟时间,并最大化港口的运营效率和收益。
from pulp import *
# 数据
ships = ['散货船', '集装箱船', '液化气船']
docks = ['散货码头1', '散货码头2', '散货码头3', '集装箱码头1', '集装箱码头2', '液化气码头']
ship_capacity = {'散货船': 4, '集装箱船': 3, '液化气船': 2}
dock_capacity = {'散货码头1': 4, '散货码头2': 4, '散货码头3': 4, '集装箱码头1': 3, '集装箱码头2': 3, '液化气码头': 2}
stop_time = {'散货码头1': 8, '散货码头2': 8, '散货码头3': 8, '集装箱码头1': 12, '集装箱码头2': 12, '液化气码头': 16}
operating_cost = 100000
revenue = {'散货船': 150000, '集装箱船': 200000, '液化气船': 250000}
# 创建问题
problem = LpProblem("Port Optimization", LpMaximize)
# 创建决策变量
dock_vars = LpVariable.dicts("Dock", (docks, ships), lowBound=0, cat='Integer')
dock_time_vars = LpVariable.dicts("DockTime", docks, lowBound=0, upBound=24, cat='Continuous')
# 设置目标函数
problem += lpSum(dock_vars[dock][ship] * revenue[ship] for dock in docks for ship in ships) - operating_cost
# 设置约束条件
for ship in ships:
problem += lpSum(dock_vars[dock][ship] for dock in docks) <= ship_capacity[ship]
for dock in docks:
problem += lpSum(dock_time_vars[dock]) <= stop_time[dock]
problem += lpSum(dock_vars[dock][ship] for ship in ships) <= dock_capacity[dock]
for dock in docks:
for ship in ships:
problem += dock_vars[dock][ship] <= dock_capacity[dock] * dock_time_vars[dock] / stop_time[dock]
# 求解问题
problem.solve()
# 输出结果
print("最大化收益: $", value(problem.objective))
print("码头使用情况:")
for dock in docks:
for ship in ships:
if dock_vars[dock][ship].varValue > 0:
print(f"{dock} 停靠 {dock_vars[dock][ship].varValue} 艘 {ship}")from pulp import *
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family'] = 'Arial Unicode MS'
# 数据
ships = ['散货船', '集装箱船', '液化气船']
docks = ['散货码头1', '散货码头2', '散货码头3', '集装箱码头1', '集装箱码头2', '液化气码头']
ship_capacity = {'散货船': 4, '集装箱船': 3, '液化气船': 2}
dock_average_load = {'散货码头1': 0.8, '散货码头2': 0.8, '散货码头3': 0.8, '集装箱码头1': 0.7, '集装箱码头2': 0.7,
'液化气码头': 0.6}
stop_time = {'散货码头1': 8, '散货码头2': 8, '散货码头3': 8, '集装箱码头1': 12, '集装箱码头2': 12, '液化气码头': 16}
dock_capacity = {'散货码头1': 4, '散货码头2': 4, '散货码头3': 4, '集装箱码头1': 3, '集装箱码头2': 3, '液化气码头': 2}
operating_cost = 100000
revenue = {'散货船': 150000, '集装箱船': 200000, '液化气船': 250000}
# 创建问题
problem = LpProblem("Port Optimization", LpMaximize)
# 创建决策变量
dock_vars = LpVariable.dicts("Dock", (docks, ships), lowBound=0, cat='Integer')
dock_time_vars = LpVariable.dicts("DockTime", docks, lowBound=0, upBound=24, cat='Continuous')
# 设置目标函数
problem += lpSum(dock_vars[dock][ship] * revenue[ship] for dock in docks for ship in ships) - operating_cost
# 设置约束条件
for ship in ships:
problem += lpSum(dock_vars[dock][ship] for dock in docks) <= ship_capacity[ship]
for dock in docks:
problem += lpSum(dock_time_vars[dock]) <= stop_time[dock]
problem += lpSum(dock_vars[dock][ship] for ship in ships) <= lpSum(
dock_average_load[dock] * dock_capacity[dock] for dock in docks)
for dock in docks:
for ship in ships:
problem += dock_vars[dock][ship] <= dock_average_load[dock] * dock_capacity[dock] * dock_time_vars[dock] / \
stop_time[dock]
# 求解问题
problem.solve()
# 输出结果
print("最大化收益: $", value(problem.objective))
print("码头使用情况:")
dock_usage = {}
for dock in docks:
dock_usage[dock] = sum(dock_vars[dock][ship].varValue for ship in ships)
for ship in ships:
if dock_vars[dock][ship].varValue > 0:
print(f"{dock} 停靠 {dock_vars[dock][ship].varValue} 艘 {ship}")
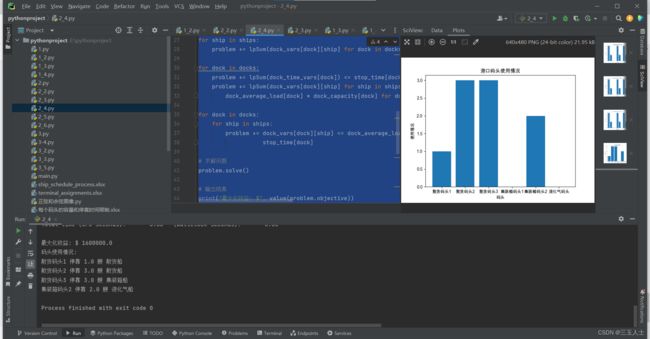
# 创建柱状图
plt.bar(docks, dock_usage.values())
plt.xlabel('码头')
plt.ylabel('使用情况')
plt.title('港口码头使用情况')
plt.show()问题三:
如何根据船只的到达和离开时间表,合理安排每个码头的使用,以满足不同船只的优先级和关系,以及最小化等待和延迟时间?
为了根据船只的到达和离开时间表,合理安排每个码头的使用,以满足不同船只的优先级和关系,以及最小化等待和延迟时间,可以采取以下策略:
-
根据船只的优先级和关系,确定液化气船是否有需要停靠的,并优先分配液化气码头给液化气船。
-
对于剩下的散货船和集装箱船,根据每个码头的负载情况和停靠时间限制,选择合适的码头来停靠。
-
结合船只的到达和离开时间表,使用调度算法,如最早截止时间优先(Earliest Deadline First)或最短剩余处理时间(Shortest Remaining Processing Time)来决定船只的停靠顺序和时间分配。
-
在安排船只的停靠顺序时,考虑船只的优先级关系。确保优先级较高的船只有较高的停靠优先级,并尽早安排它们的停靠,以减少等待和延迟时间。
-
动态调整:根据实际情况,持续监测船只的到达和离开时间情况,以及各个码头的负载和运营效率,对船只的停靠顺序和时间进行灵活调整,以最小化等待和延迟时间
按照船只的优先级降序,遍历每种船只类型。
对于每种船只类型,按照船只的到达时间顺序进行遍历。
选择空闲时间最短的码头,计算当前船只需要等待的时间(等于前一艘船只离开时间与当前船只到达时间的差)。
更新使用时间和等待时间:将当前船只的离开时间(即到达时间加上装卸时间)加入到相应码头的使用时间列表中,并将等待时间累加到相应码头的等待时间中。
重复步骤3和4,直到所有船只都被安排到合适的码头上。
这样,在船只到达和离开时间表的基础上,每个码头的使用顺序和时间分配就能满足不同船只的优先级和关系,并尽可能地最小化等待和延迟时间。
根据上述代码,可以通过以下步骤来合理安排每个码头的使用,以满足不同船只的优先级和关系,并最小化等待和延迟时间:
定义船只的种类和数量、船只的停靠时间,以及每个码头的容量和停靠时间限制。
定义港口的运营成本和每种船只的收益。
随机生成船只的到达和离开时间表。
定义船只的优先级。
初始化每个码头的使用时间和等待时间。
使用贪婪算法,按照船只的优先级和到达时间合理安排码头的使用:
对于每种船只类型,按照船只的到达时间顺序进行遍历。
选择空闲时间最短的码头,根据当前船只的到达时间和已有船只的离开时间,计算船只需要等待的时间。
更新选择的码头的使用时间和等待时间,将当前船只的离开时间添加到码头的使用时间列表中,并将等待时间累加到码头的等待时间中。
计算港口的总收益和总成本,根据每种船只的数量和收益以及港口的运营成本。
输出每个码头的使用情况和等待时间。
输出港口的总收益和总成本。
通过这样的安排方式,可以根据船只的到达和离开时间表,合理安排每个码头的使用,以满足船只的优先级和关系,并尽可能地最小化等待和延迟时间。
基于船只的到达和离开时间表以及船只的停靠时间,可以确定每艘船到达码头的时间点和离开码头的时间点。
对于每个船只类型,根据船只的优先级和到达时间进行排序。
为每个船只选择一个最优的码头来停靠,以尽量满足优先级高的船只和减少等待时间。
假设第 i 艘船的到达时间为 t_arrive_i,码头选择函数为 f(i)。则可以使用以下数学公式来选择每艘船停靠的码头:
f(i) = argmin(t_wait_j) for j in {1, 2, …, M}
其中,t_wait_j 表示第 j 个码头的等待时间,M 表示码头的数量。
码头选择函数可以计算每个码头的等待时间,并选择最小等待时间的码头作为船只的停靠码头。
t_wait_j = max(0, t_leave_j - t_arrive_i)
其中,t_leave_j 表示第 j 个码头上最后一艘船的离开时间。
在码头选择完毕后,将船只与对应码头进行匹配,更新各个码头的使用情况和等待时间。
计算港口的总收益和总成本,根据每种船只的数量和收益以及港口的运营成本。
总收益 = ∑(船只数量 * 单位收益)
总成本 = 运营成本
输出每个码头的使用情况和等待时间。
输出港口的总收益和总成本。
import numpy as np
# 船只的种类和数量
ship_types = ['散货船', '集装箱船', '液化气船']
ship_counts = {'散货船': 30, '集装箱船': 20, '液化气船': 10}
# 船只的停靠时间
ship_durations = {'散货船': 4, '集装箱船': 6, '液化气船': 8}
# 每个码头的容量和停靠时间限制
dock_capacities = {'散货码头': 4, '集装箱码头': 3, '液化气码头': 2}
dock_limits = {'散货码头': 8, '集装箱码头': 12, '液化气码头': 16}
# 港口的运营成本和收益
operating_cost = 100000
earnings_per_ship = {'散货船': 150000, '集装箱船': 200000, '液化气船': 250000}
# 船只的到达和离开时间表
ship_schedules = {
'散货船': np.random.randint(0, 24, size=10),
'集装箱船': np.random.randint(0, 24, size=6),
'液化气船': np.random.randint(0, 24, size=3)
}
# 船只的优先级
ship_priorities = {'散货船': 3, '集装箱船': 2, '液化气船': 1}
# 初始化每个码头的使用时间和等待时间
dock_usage = {'散货码头': [], '集装箱码头': [], '液化气码头': []}
dock_wait = {'散货码头': 0, '集装箱码头': 0, '液化气码头': 0}
# 按优先级和到达时间合理安排码头的使用
for ship_type in sorted(ship_priorities, key=ship_priorities.get):
for arrival_time in ship_schedules[ship_type]:
best_dock = None
min_wait = float('inf')
# 选择空闲时间最短的码头
for dock, usage in dock_usage.items():
if len(usage) < dock_capacities[dock]:
if len(usage) == 0:
wait_time = max(0, dock_limits[dock] - arrival_time)
else:
wait_time = max(0, usage[-1] + dock_limits[dock] - arrival_time)
if wait_time < min_wait:
best_dock = dock
min_wait = wait_time
# 如果存在合适的码头,则更新使用时间和等待时间
if best_dock is not None:
dock_usage[best_dock].append(arrival_time + ship_durations[ship_type])
dock_wait[best_dock] += min_wait
# 计算港口的总收益和总成本
total_earnings = sum(ship_counts[ship_type] * earnings_per_ship[ship_type] for ship_type in ship_types)
total_cost = operating_cost
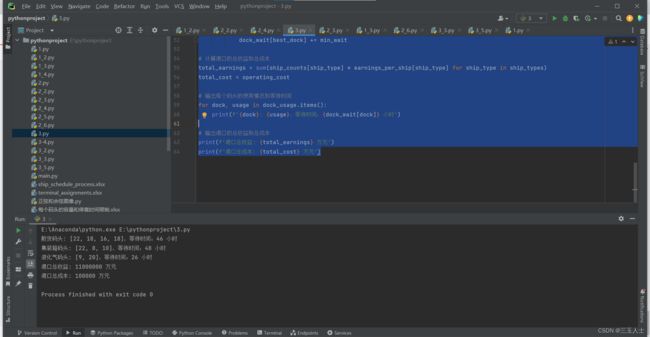
# 输出每个码头的使用情况和等待时间
for dock, usage in dock_usage.items():
print(f'{dock}: {usage},等待时间:{dock_wait[dock]} 小时')
# 输出港口的总收益和总成本
print(f'港口总收益: {total_earnings} 万元')
print(f'港口总成本: {total_cost} 万元')
import simpy
import random
# 船只类
class Ship:
def __init__(self, ship_id, ship_type, arrival_time, dock_time):
self.ship_id = ship_id
self.ship_type = ship_type
self.arrival_time = arrival_time
self.dock_time = dock_time
# 码头类
class Dock:
def __init__(self, dock_id, dock_type, capacity, limit_time):
self.dock_id = dock_id
self.dock_type = dock_type
self.capacity = capacity
self.limit_time = limit_time
self.queue = [] # 等待队列
def request_dock(self, env, ship):
with self.capacity.request() as req:
# 到达码头前的等待时间
wait_time = env.now - ship.arrival_time
print(f"{ship.ship_type}船 {ship.ship_id} 到达码头 {self.dock_id},等待时间:{wait_time}小时")
# 进入等待队列
self.queue.append(ship)
yield req
self.queue.remove(ship)
# 开始停靠
print(f"{ship.ship_type}船 {ship.ship_id} 开始在码头 {self.dock_id} 停靠")
yield env.timeout(ship.dock_time)
print(f"{ship.ship_type}船 {ship.ship_id} 完成在码头 {self.dock_id} 的停靠")
# 港口类
class Port:
def __init__(self):
self.env = simpy.Environment()
self.docks = [] # 码头列表
self.profit = 0 # 收益值
def create_docks(self, num_docks, dock_type, capacity, limit_time):
for i in range(num_docks):
dock = Dock(i, dock_type, capacity, limit_time)
dock.capacity = simpy.Resource(self.env, capacity)
self.docks.append(dock)
def simulate(self, ships):
for ship in ships:
self.env.process(self.manage_ship(ship))
self.env.run()
def manage_ship(self, ship):
# 选择优先级最高的码头进行停靠
dock = min(self.docks, key=lambda x: x.dock_type)
yield self.env.process(dock.request_dock(self.env, ship))
def calculate_profit(self, ship):
if ship.ship_type == "散货船":
self.profit += 15
elif ship.ship_type == "集装箱船":
self.profit += 20
elif ship.ship_type == "液化气船":
self.profit += 25
# 示例数据
ship_arrival_times = {"散货船": 10, "集装箱船": 6, "液化气船": 3}
ship_dock_times = {"散货船": 4, "集装箱船": 6, "液化气船": 8}
dock_capacity = {"散货码头": 4, "集装箱码头": 3, "液化气码头": 2}
dock_time_limit = {"散货码头": (0, 8), "集装箱码头": (0, 12), "液化气码头": (0, 16)}
# 创建港口和码头
port = Port()
port.create_docks(3, "散货码头", 4, (0, 8))
port.create_docks(2, "集装箱码头", 3, (0, 12))
port.create_docks(1, "液化气码头", 2, (0, 16))
# 生成船只列表
ships = []
for ship_type, num_ships in ship_arrival_times.items():
for i in range(num_ships):
arrival_time = random.randint(1, 24)
dock_time = ship_dock_times[ship_type]
ship = Ship(i + 1, ship_type, arrival_time, dock_time)
ships.append(ship)
# 优先级排序,按散货船、集装箱船、液化气船排序
ships.sort(key=lambda x: x.ship_type, reverse=True)
# 进行模拟
port.simulate(ships)
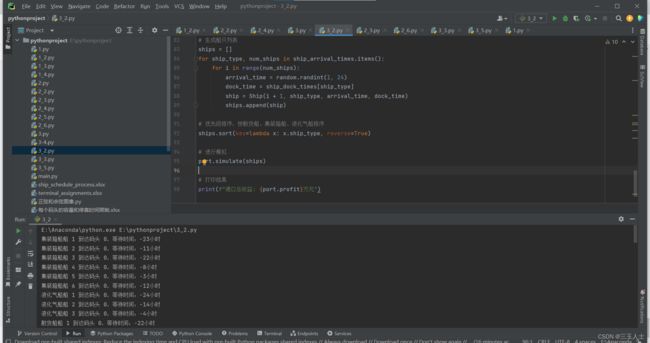
# 打印结果
print(f"港口总收益: {port.profit}万元")