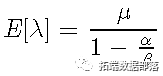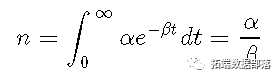R语言和Python用泊松过程扩展:霍克斯过程Hawkes Processes分析比特币交易数据订单到达自激过程时间序列...
全文下载链接:http://tecdat.cn/?p=25880
本文描述了一个模型,该模型解释了交易的聚集到达,并展示了如何将其应用于比特币交易数据。这是很有趣的,原因很多。例如,对于交易来说,能够预测在短期内是否有更多的买入或卖出是非常有用的。另一方面,这样的模型可能有助于理解基本新闻驱动价格与机器人交易员对价格变化的反应之间的区别(点击文末“阅读原文”获取完整代码数据)。
介绍
订单到达的自激性和集群性
交易不会以均匀的间隔到达,但通常会在时间上聚集在一起。类似地,相同的交易标志往往会聚集在一起并产生一系列买入或卖出订单。 例如,将订单分成小块的算法交易者或对某些交易所事件做出反应的交易系统。
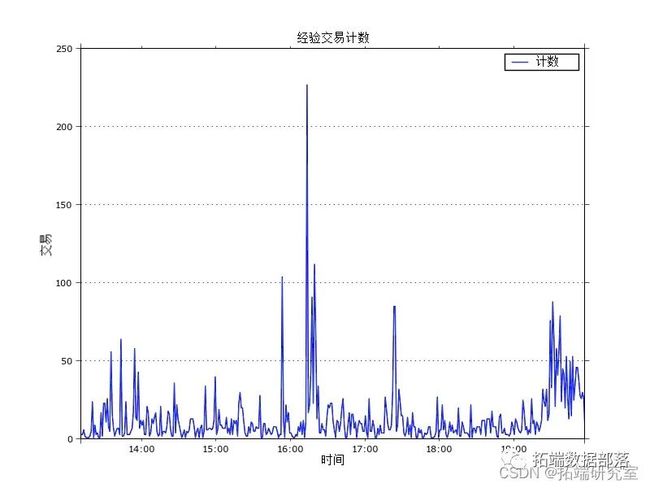
出于演示目的,我使用的数据是 2013 年 4 月 20 日 13:10 到 19:57 之间的 5000 笔交易。这是 1 分钟窗口内聚合的交易计数图。
plot(x, b, type = "l")每分钟的平均交易数是 13,但是我们可以找出几个超过 50 的实例。通常较高的交易强度会持续几分钟,然后再次下降到平均值。特别是在 16:00 之后的 15 分钟左右,我们可以看到非常高的交易强度,其中一个实例每分钟超过 200 个订单,然后在接下来的约 10 分钟内强度缓慢下降。
描述事件计数到达的最基本方法,例如上面的时间序列,是泊松过程 ,有一个参数λ。在泊松过程中,每单位时间的预期事件数由一个参数定义。这种方法被广泛使用,因为它非常适合大量数据,例如呼叫中心的电话到达。然而,就我们的目的而言,这太简单了,因为我们需要一种方法来解释聚类和均值回归。
霍克斯过程(Hawkes Processes),是基本泊松过程的扩展,旨在解释这种聚类。像这样的自激模型广泛用于各种科学;一些例子是地震学(地震和火山喷发的建模)、生态学(野火评估 )、神经科学,当然还有金融和贸易。
让我们继续理解和拟合霍克斯过程(Hawkes Processes)到上面的数据。
霍克斯过程(Hawkes Processes)
霍克斯过程对随时间变化的强度或过程的事件发生率进行建模,这部分取决于过程的历史。另一方面,简单的泊松过程没有考虑事件的历史。
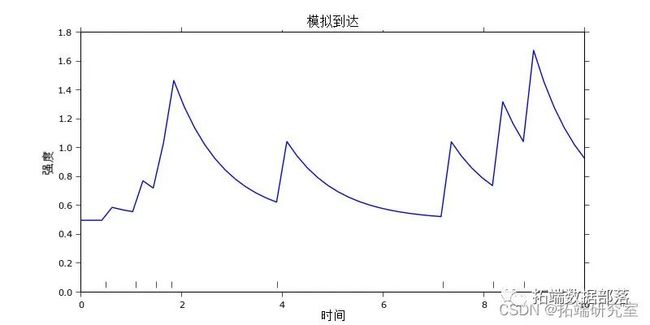
下图中绘制了霍克斯过程的示例实现。
它由 8 个事件组成,通常采用时间戳的形式,以及由三个参数定义的样本强度路径
这里,μ是过程恢复到的基本速率,α是事件发生后的强度跳跃,β是指数强度衰减。基准率也可以解释为外生事件的强度,例如新闻。其他参数 α 和 β 定义了过程的聚类属性。通常情况下 α<β 确保强度降低的速度快于新事件增加的速度。
点击标题查阅往期内容
R语言连续时间马尔科夫链模拟案例 Markov Chains
![]()
左右滑动查看更多
![]()
01
02
03
04
自我激发性在时间标记 2 之前的前四个事件中是可见的。它们在彼此相距很短的时间内发生,这导致第四个事件的强度峰值很大。每一次事件的发生都会增加另一次发生的机会,从而导致事件的聚集。第五个数据点仅在时间标记 4 处到达,与此同时,导致整体强度呈指数下降。
条件强度最简单的形式是
指数函数定义了过程的记忆,即过去的事件如何影响当前的事件。求和将此函数应用于从事件 titi 到当前事件 t 的历史。λ(t)表示时间 t 的瞬时强度。
给定条件强度,两个派生量也很有趣:期望强度(在某些条件下)可以显示为 [4] 具有以下形式
并描述给定时间段的交易强度。另一个量是所谓的分支比
它描述了内生产生的交易比例(即作为另一笔交易的结果)。这可以用来评估交易活动中有多少是由反馈引起的。
可以使用传统的最大似然估计和凸求解器来拟合模型的参数。
将比特币交易的到来与霍克斯过程相匹配
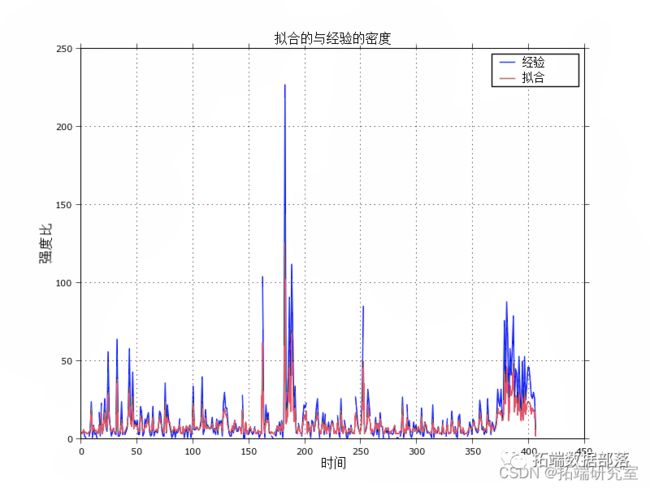
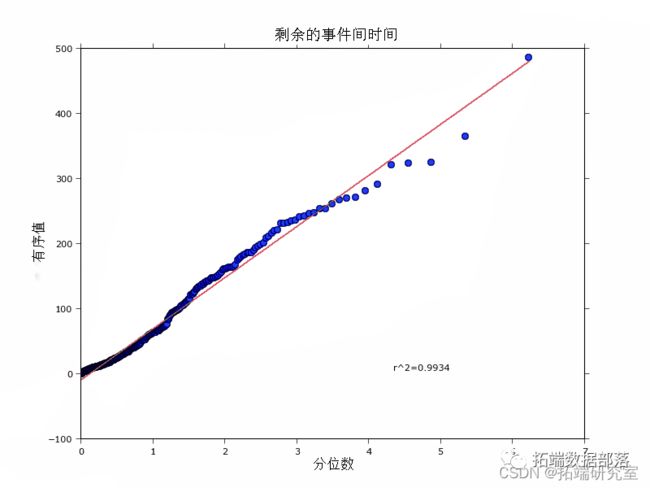
在给定一组有序交易时间 t1 我通过将存储在数据帧中的 5000 个交易时间戳传递给它来运行上面的拟合过程。与原始数据集的唯一区别是我为与另一笔交易共享时间戳的所有交易添加了一个随机毫秒时间戳。这是必需的,因为模型需要区分每笔交易(即每笔交易必须有唯一的时间戳)。文献描述了解决这个问题的不同方法 [4, 10],但将时间戳扩展到毫秒是一种常见的方法。 我们最终得到的参数估计为 μ=0.07,α=1.18,β=1.79。α 的参数估计表明,在单笔交易发生后,条件强度每秒增加 1.18 笔交易。此外,整个期间的平均强度为每秒 E[λ]=0.20次交易,一分钟内总共有 12 次交易,这与我们的经验计数相符。n=65%的分支率表明超过一半的交易是在模型内作为其他交易的结果产生的。鉴于所研究的时间相对平稳,价格呈上涨趋势,这一数字很高。将其应用于更动荡的区制或状态(例如一些崩溃)会很有趣,我认为该比率会高得多。 现在的目的是计算拟合模型的实际条件强度,并将其与经验计数进行比较。R 执行此评估,我们只需提供一系列时间戳即可对其进行评估。该范围介于原始数据集的最小和最大时间戳之间,对于该范围内的每个点,都会计算瞬时强度。 下图比较经验计数(来自本文的第一个图)和拟合的综合强度。 从图上看,这似乎是一个相当好的拟合。请注意,历史强度往往高于拟合的强度。可以通过引入有影响和无影响的交易来解决这个问题,这有效地减少了作为拟合程序一部分的交易数量。经验数据和拟合数据之间跳跃大小略微不匹配的另一个原因可能是同一秒内时间戳的随机化;在5000个原始交易中,超过2700个交易与另一个交易共享一个时间戳。这导致大量的交易(在同一秒内)失去订单,这可能会影响跳跃的大小。 拟合优度 评估拟合优度的方法有很多种。一种是通过比较AIC同质泊松模型的值,如上面的 R 总结中所示,我们的霍克斯模型更适合数据。 检验模型与数据拟合程度的另一种方法是评估残差。理论上说[4],如果模型拟合得好,那么残差过程应该是同质的,应该有事件间时间(两个残差事件时间戳之间的差值),这些时间是指数分布。事件间时间的对数图,或者在我们的案例中,对指数分布的QQ图,证实了这点。下面的图显示了一个很好的R2拟合。 现在我们知道该模型很好地解释了到达的聚类,那么如何将其应用于交易呢?下一步将是至少单独考虑买入和卖出的到达,并找到一种方法来预测给定的霍克斯模型。然后,这些强度预测可以构成做方向性策略的一部分。让我们看一下文献以获得一些想法。 Hewlett[2]使用买入和卖出到达之间的双变量自激和交叉激振过程,预测了未来买入和卖出交易的不平衡性。作者设计了一个最佳的清算策略,由一个基于这种不平衡的价格影响公式得出。 在文献[3]中,作者使用双变量霍克斯过程的买入和卖出强度比作为进行方向性交易的进入信号。 Hawkes 过程的对数似然函数具有 O(N2) 的计算复杂度,因为它在交易历史中执行嵌套循环。仍然是低效的,特别是对于高频交易目的。 在本文中,我展示了霍克斯过程是解释 交易的聚集到达的一个很好的模型。我展示了如何在给定交易时间戳的情况下估计和评估模型,并强调了一些与估计有关的问题。 比特币交易数据及其价格发现尚未得到很好的研究。自激模型可能会回答诸如比特币价格变动有多少是由基本事件引起的等问题。该模型本身自然也可以成为交易策略的一部分。 [1] J. Fonseca 和 R. Zaatour:霍克斯过程:快速校准、贸易聚类和扩散限制的应用 ssrn. [2] P. Hewlett:订单到达聚类、价格影响和交易路径优化 pdf. [3] J. Carlsson、M. Foo、H. Lee、H. Shek:使用双变量霍克斯过程进行高频交易预测。 本文摘选《R语言和Python用泊松过程扩展:霍克斯过程Hawkes Processes分析比特币交易数据订单到达自激过程时间序列》,点击“阅读原文”获取全文完整资料。 点击标题查阅往期内容 指数加权模型EWMA预测股市多变量波动率时间序列 R语言极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR:多元化投资组合预测风险测度分析 R语言GARCH-DCC模型和DCC(MVT)建模估计 Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列 R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格 R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列 Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测 R语言时间序列GARCH模型分析股市波动率 R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测 matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计 Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测 使用R语言对S&P500股票指数进行ARIMA + GARCH交易策略 R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模 R语言股票市场指数:ARMA-GARCH模型和对数收益率数据探索性分析 R语言多元Copula GARCH 模型时间序列预测 R语言使用多元AR-GARCH模型衡量市场风险 R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格 R语言用Garch模型和回归模型对股票价格分析 GARCH(1,1),MA以及历史模拟法的VaR比较 matlab估计arma garch 条件均值和方差模型 R语言POT超阈值模型和极值理论EVT分析 R语言极值推断:广义帕累托分布GPD使用极大似然估计、轮廓似然估计、Delta法 R语言极值理论EVT:基于GPD模型的火灾损失分布分析 R语言有极值(EVT)依赖结构的马尔可夫链(MC)对洪水极值分析 R语言POT超阈值模型和极值理论EVT分析 R语言混合正态分布极大似然估计和EM算法 R语言多项式线性模型:最大似然估计二次曲线 R语言Wald检验 vs 似然比检验 R语言GARCH-DCC模型和DCC(MVT)建模估计 R语言非参数方法:使用核回归平滑估计和K-NN(K近邻算法)分类预测心脏病数据 matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计 R语言基于Bootstrap的线性回归预测置信区间估计方法 R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型 Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型 Matlab马尔可夫区制转换动态回归模型估计GDP增长率 R语言极值推断:广义帕累托分布GPD使用极大似然估计、轮廓似然估计、Delta法 R语言中实现马尔可夫链蒙特卡罗MCMC模型 matlab贝叶斯隐马尔可夫hmm模型实现 R语言如何做马尔科夫转换模型markov switching model matlab中的隐马尔可夫模型(HMM)实现 R语言马尔可夫体制转换模型Markov regime switching R语言马尔可夫转换模型研究交通伤亡人数事故预测 R语言中的马尔科夫机制转换(Markov regime switching)模型 用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)股票指数预测实战 用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用 R语言中实现马尔可夫链蒙特卡罗MCMC模型 用R语言模拟M / M / 1随机服务排队系统 用R语言模拟混合制排队随机服务排队系统 用R语言模拟M/M/1随机服务排队系统fhawks <- function(data) {
# 初始猜测,a是α,C是β
pstt <- c
# 使用条件强度函数创建一个对象
proc
# 假设强度必须是正的
conditi <- penaltany(parms < 0)
# 使用标准优化法进行拟合
fit(m, optrol = list(trace = 2))summary(f)申请交易
改进
结论
参考
![]()
![]()