最短路 - Dijkstra算法 && 堆优化版

最短路 - Dijkstra算法

思路：

该算法常用于求只含有正边权的单源最短路。
采用 贪心策略，以1节点为起点，每次选取连通块外延的最短边和对应的点放入连通块，再更新新的连通块外延的边。连通部分逐渐扩大，最后一直走到n节点。
时间复杂度：O( n ^ 2 )，应用于稠密图。

伪代码 / 模板：

int Dijkstra(){
	memset(dist,INF,sizeof dist);
	dist[1]=0; //起点到起点的距离为 0

	for(int i=0;i<n;i++){
		int hp=-1;
		for(int j=1;j<=n;j++){
			if(!st[j]&&(hp==-1||dist[hp]>dist[j])) //没走到过 且是可走到的节点中最短的
				hp=j;
		}
		st[hp]=1; //走到了 打个标记
		for(int j=1;j<=n;j++) //更新外延边
			dist[j]=min(dist[j],dist[hp]+mp[hp][j]);
	}
	
	if(dist[n]==INF) //没走到 n节点，路径不存在
 		return -1;
	else
		return dist[n];
}

---

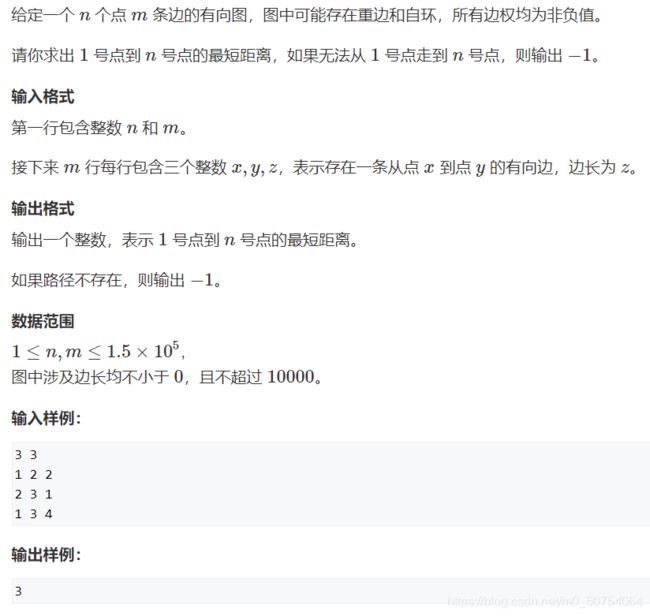
模板题：AcWing849. Dijkstra求最短路 I

题面：【传送门】

思路：

模板题还需要思路？ 见前文模板代码注释。

AC代码：

#include
#include
using namespace std;
const int N=505;
const int INF=0x3f3f3f3f;

int n,m;
int mp[N][N];
int dist[N];
bool st[N];

int Dijkstra(){
	memset(dist,INF,sizeof dist);
	dist[1]=0;

	for(int i=0;i<n;i++){
		int hp=-1;
		for(int j=1;j<=n;j++){
			if(!st[j]&&(hp==-1||dist[hp]>dist[j]))
				hp=j;
		}
		st[hp]=1;
		for(int j=1;j<=n;j++)
			dist[j]=min(dist[j],dist[hp]+mp[hp][j]);
	}
	
	if(dist[n]==INF)	
		return -1;
	else
		return dist[n];
}


int main(){
	
	//freopen("D:\\in.txt","r",stdin);
	
	cin>>n>>m;
	
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			mp[i][j]=INF;
	
	int u,v,w;
	for(int i=0;i<m;i++){
		scanf("%d%d%d",&u,&v,&w);
		mp[u][v]=min(mp[u][v],w);
	}
	
	cout<<Dijkstra();
	
	return 0;
}

---

最短路 - Dijkstra算法 ( 堆优化版 )

思路：

该算法常用于求只含有正边权的单源最短路。
通过小根堆来维护当前未到达 (未标记 ) 且离连通块最近的点，放入并更新
时间复杂度：O( m * logn )，应用于稀疏图。

伪代码 / 模板：

int dijkstra(){
	memset(dist,INF,sizeof dist);
	dist[1]=0; //起点
	priority_queue<PII ,vector<PII> ,greater<PII> > heap; //小根堆（优先队列）
	
	heap.push({0,1});
	while(heap.size()){
		PII k=heap.top();
		heap.pop();
		int dis=k.first;
		int hp=k.second;
		
		if(st[hp]) //走过了
			continue;
		st[hp]=1;
		
		for(int i=h[hp];i!=-1;i=ne[i]){ //更新外延路
			int t=e[i];  //i是下标，e中存的是i这个下标对应的点。
			if(dist[t]>dis+w[i]){
				dist[t]=dis+w[i];
				heap.push({dist[t],t}); 
			}
		}
	}
	
	if(dist[n]==INF) //没走到
		return -1;
	else
		return dist[n];
}

---

模板题：AcWing850. Dijkstra求最短路 II

题面：【传送门】

思路：

模板题还需要思路？ 见前文模板代码注释。
稀疏图用邻接表来存

AC代码：

#include
#include
#include 
using namespace std;
const int N=150005;
const int INF=0x3f3f3f3f;
typedef pair<int,int> PII;

int n,m;
int e[N],ne[N],w[N],h[N],idx; 
int dist[N];
bool st[N];

void add(int x,int y,int c){
	w[idx]=c;
	e[idx]=y;
	ne[idx]=h[x];
	h[x]=idx++;
}

int dijkstra(){
	memset(dist,INF,sizeof dist);
	dist[1]=0;
	priority_queue<PII ,vector<PII> ,greater<PII> > heap;
	
	heap.push({0,1});
	
	while(heap.size()){
		PII k=heap.top();
		heap.pop();
		int dis=k.first;
		int hp=k.second;
		
		if(st[hp])
			continue;
		st[hp]=1;
		
		for(int i=h[hp];i!=-1;i=ne[i]){
			int t=e[i];
			if(dist[t]>dis+w[i]){
				dist[t]=dis+w[i];
				heap.push({dist[t],t}); 
			}
		}
	}
	
	if(dist[n]==INF)
		return -1;
	else
		return dist[n];
}

int main(){
	//freopen("D:\\in.txt","r",stdin);
	
	memset(h,-1,sizeof h);
	cin>>n>>m;
	
	int u,v,c;
	for(int i=0;i<m;i++){
		scanf("%d%d%d",&u,&v,&c);
		add(u,v,c);
	}
	
	cout<<dijkstra();
	return 0;
}

补充：

若要求点i到点j的最短距离，只需修改dijkstra方法中的起源位置dist[i] = 0，以及返回为dist[j]