机器学习的第一节基本概念的相关学习

目录

1.1 决策树的概念

1.2 KNN的概念

1.2.1KNN的基本原理

1.2.2 流程：

1.2.3 优缺点

1.3 深度学习

1.4 梯度下降

损失函数

1.5 特征与特征选择

特征选择的目的

1.6 python中dot函数总结

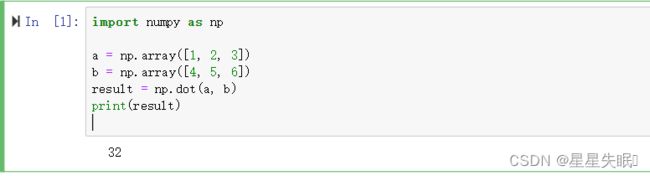
一维数组的点积：

二维数组（矩阵）的乘法：

多维数组的乘法：

---

1.1 决策树的概念

        决策树（decision tree）是一种基本的分类与回归方法。决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。

        决策树是一种描述对实例进行分类的树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果，本质是一颗由多个判断节点组成的树。分类决策树模型是一种树形结构。 决策树由结点和有向边组成。结点有两种类型：内部结点和叶节点。内部结点表示一个特征或属性，叶节点表示一个类。

1.2

1.2 KNN的概念

 K-NearestNeighbor简称KNN,中文名K最近邻，其作用通俗来说就是将数据集合中每一个样本进行分类的方法，机器学习常用算法之一，属于有监督分类算法。

1.2.1KNN的基本原理

如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。   

简单理解就是：   简单来说就是设定k值，取样本点范围最近的k个点，其中哪类数量最多则预测的点就为那一类

1.2.2 流程：

1） 计算已知类别数据集中的点与当前点之间的距离
2） 按距离递增次序排序
3） 选取与当前点距离最小的k个点
4） 统计前k个点所在的类别出现的频率
5） 返回前k个点出现频率最高的类别作为当前点的预测分类

  1、K值的选定

        通过交叉验证（将样本数据按照一定比例，拆分出训练用的数据和验证用的数据，比如6：4拆分出部分训练数据和验证数据），从选取一个较小的 K 值开始，不断增加 K 的值，然后计算验证集合的方差，最终找到一个比较合适的 K 值。

1.2.3 优缺点

优点：
1、简单易用，对异常值不敏感
2、重新训练代价低
3、算法复杂度低
4、适合类域交叉样本
5、适用大样本自动分类

特点：非参数的，惰性的算法模型即：不会对数据做出任何假设，而线性回归总会假设一条直线，惰性的意思是没有明确的训练数据过程，或者过程很短不像逻辑回归需要先对数据进行大量的训练

缺点：
1、对内存要求较高
2、类别分类不标准化
3、输出可解释性不强
4、不均衡性
5、计算量较大 
6、惰性学习，预测阶段可能会慢，对不相关的功能和数据规模敏感
 

1.3 深度学习

深度学习是在机器学习之后=要学习的课程，要知道深度学习和神经网络有关系，比如说那个下棋的机器人就用到了神经网络。

1. 深度学习是机器学习的一个分支(最重要的分支)
2. 机器学习是人工智能的一个分支

深度学习的概念源于人工神经网络的研究，但是并不完全等于传统神经网络。

不过在叫法上，很多深度学习算法中都会包含"神经网络"这个词，比如：卷积神经网络、循环神经网络。

所以，深度学习可以说是在传统神经网络基础上的升级，约等于神经网络。

1.4 梯度下降

在生活中，我们可以通过一个简单的例子来说明梯度下降的概念。
假设你是一位学生，每天早上需要赶去上学。你发现离学校的距离与你起床的时间之间存在着某种关系。你想找到一个起床时间，使得你花费的时间最短，也就是找到最优的起床时间。
你开始进行实验，每天记录自己起床的时间和到达学校所需的时间。你建立了一个简单的模型，假设到达学校的时间与起床时间之间存在线性关系，即到达学校的时间等于起床时间乘以一个参数k，再加上一个常数b，即到达学校的时间等于k * 起床时间 + b。
现在的问题是，如何通过梯度下降算法来找到最优的起床时间，使得到达学校的时间最短。
首先，你需要收集一些数据，包括起床时间和到达学校的时间。假设你收集了一周的数据。
然后，你需要定义一个损失函数，用于衡量到达学校时间与实际记录之间的差距。可以选择均方误差作为损失函数，即将每天的差距平方后求和再除以天数。
接下来，你随机初始化起床时间参数k和常数b的值。
然后，通过梯度下降算法进行迭代更新。根据梯度下降算法的原理，你需要计算损失函数对于起床时间参数k和常数b的偏导数，并根据学习率进行参数的更新。
在每次迭代中，你将根据实际数据计算损失函数，并通过梯度下降算法不断调整起床时间的参数k和常数b，使得损失函数逐渐减小，直到收敛到一个最优解。
最后，当损失函数收敛到一个较小的值时，你就找到了最优的起床时间，使得到达学校的时间最短。
通过这个例子，你可以理解梯度下降算法在寻找最优解的过程中的应用。在生活中，我们可以通过这种迭代、优化的方式来改进自己的决策和行为，以获得更好的结果。

损失函数

在机器学习和优化问题中，损失函数（Loss Function）是用来衡量模型预测值与真实值之间的差距或误差的函数。它是模型训练中的关键组成部分，用于评估模型的性能并指导参数的优化。

1.5 特征与特征选择

在机器学习中，将属性称为“特征（Feature）”，对当前学习任务有用的属性称为“相关特征（Relevant Feature）”，没有什么用的属性称为“无关特征（Irrelevant Feature）”。从给定的特征集合中选择出相关特征子集的过程，称为“特征选择（Feature Selection）”

特征选择是一个重要的数据预处理过程。在现在的机器学习中，获得数据之后通常先进行特征选择，此后再训练学习器。

特征选择过程必须确保不丢失重要特征，否则后续学习过程会因为重要信息的缺失而无法获得好的性能。给定数据集，若学习任务不同，则相关特征很可能不同。

另外，有一类特征称为“冗余特征（Redundant Feature）”，它们所包含的信息能从其它特征中推演出来。那么，去除冗余特征会减轻学习过程的负担。

特征选择的目的

在机器学习的实际应用中，特征数量往往较多，其中可能存在不相关的特征，特征之间也可能存在相互依赖，容易导致如下的后果：

特征个数越多，分析特征、训练模型所需的时间就越长。
特征个数越多，容易引起“维度灾难”，模型也会越复杂，其推广能力会下降。
特征选择能剔除不相关(irrelevant)或冗余(redundant )的特征，从而达到减少特征个数，提高模型精确度，减少运行时间的目的。另一方面，选取出真正相关的特征简化了模型，使研究人员易于理解数据产生的过程。

特征选择主要有两个目的：

减少特征数量、降维，避免维度灾难，这样能使模型泛化能力更强，减少过拟合，缩短模型训练时间。
增强对特征和特征值之间的理解

两个特征的时候还有图像，三个特征的时候就没有图像了，是一个面，四个特征得靠推导

降维就是降特征

1.6 python中dot函数总结

在NumPy中，dot函数用于计算两个数组的点积（内积）或矩阵乘法。dot函数的用法有一些细微的差别，取决于输入的数组是一维数组、二维数组（矩阵）还是多维数组。

一维数组的点积：

在这个例子中，dot函数计算了两个一维数组a和b的点积，即14 + 25 + 3*6 = 32。

二维数组（矩阵）的乘法：

在这个例子中，dot函数计算了两个二维数组（矩阵）A和B的矩阵乘法

多维数组的乘法：

1. 在这个例子中，dot函数计算了两个三维数组的乘法。

需要注意的是，dot函数在进行矩阵乘法时，要求第一个数组的列数与第二个数组的行数相等