排序算法学习
总体概况
参考自:https://github.com/hustcc/JS-Sorting-Algorithm
排序算法是《数据结构与算法》中最基本的算法之一。
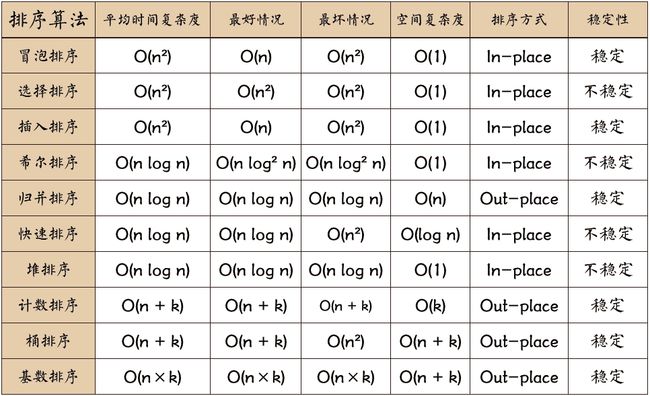
排序算法可以分为内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括:
关于时间复杂度:
- 平方阶 (O(n2)) 排序 各类简单排序:直接插入、直接选择和冒泡排序。
- 线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序;
- O(n1+§)) 排序,§ 是介于 0 和 1 之间的常数。 希尔排序
- 线性阶 (O(n)) 排序 基数排序,此外还有桶、箱排序。
关于稳定性:
稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序。
冒泡排序
1.概念
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
作为最简单的排序算法之一,冒泡排序给我的感觉就像 Abandon 在单词书里出现的感觉一样,每次都在第一页第一位,所以最熟悉。冒泡排序还有一种优化算法,就是立一个 flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用。
2.算法步骤
-
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
-
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
3.动图演示
https://github.com/hustcc/JS-Sorting-Algorithm/blob/master/res/bubbleSort.gif
4.时间
当输入是正序时最快,反序时最慢
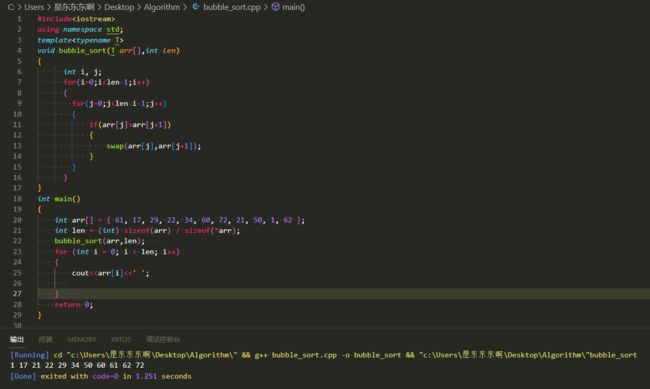
5.代码
#include
using namespace std;
template
void bubble_sort(T arr[],int len)
{
int i, j;
for(i=0;iarr[j+1]) //相邻元素对比
{
swap(arr[j],arr[j+1]); //交换位置
}
}
}
}
int main()
{
int arr[] = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 };
int len = (int) sizeof(arr) / sizeof(*arr);
bubble_sort(arr,len);
for (int i = 0; i < len; i++)
{
cout< 选择排序
1.概念
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
2.算法步骤
-
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
-
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
-
重复第二步,直到所有元素均排序完毕。
3.代码:
#include
#include
using namespace std;
template
void selection_sort(std::vector &arr)
{
for(int i=0;i arr = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 };
selection_sort(arr);
for (int i = 0; i < arr.size(); i++)
{
cout< 插入排序
1.概念
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
2. 算法步骤
-
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
-
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
3.代码:
#include
#include
using namespace std;
template
//vector arr = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 };
void insertion_sort(std::vector &arr)
{
for(int i=1;i=0)&&(squence arr = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 };
insertion_sort(arr);
for(int i=0;i 希尔排序
1.概念
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。它是插入排序的高级版。
2.算法步骤
希尔排序:将无序数组分割为若干个子序列,子序列不是逐段分割的,而是相隔特定的增量的子序列,对各个子序列进行插入排序;然后再选择一个更小的增量,再将数组分割为多个子序列进行排序......最后选择增量为1,即使用直接插入排序,使最终数组成为有序。
增量的选择:在每趟的排序过程都有一个增量,至少满足一个规则 增量关系 d[1] > d[2] > d[3] >..> d[t] = 1 (t趟排序);根据增量序列的选取其时间复杂度也会有变化,这个不少论文进行了研究,在此处就不再深究; 本文采用首选增量为n/2,以此递推,每次增量为原先的1/2,直到增量为1;
下图详细讲解了一次希尔排序的过程。
自我理解:将元素分成若干组,对每一组进行插入排序。提高了插入排序的效率。
3.代码:
#include
#include
using namespace std;
template
void shell_sort(std::vector &array, int length) {
for(int h=length/2;h>0;h=h/2) //按照(二分或者三分)增量将数组分成n组
{
//插入排序每个小分组
for(int i=0;i=0&&(array[j-h]>array[j]))
{
std::swap(array[j-h],array[j]);
j=j-h;
}
}
}
}
for(int i=0;i arr = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 };
int length = arr.size();
shell_sort(arr,length);
return 0;
}