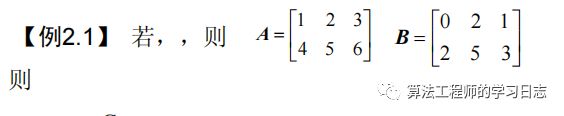Simulink建模与仿真(3)-Simulink使用基础(Matlab内容)
分享一个系列,关于Simulink建模与仿真,尽量整理成体系
1、MATLAB的计算单元:向量与矩阵
MATLAB作为一个高性能的科学计算平台,主要面向高级科学计算。MATLAB的基本计算单元是矩阵与向量,向量为矩阵的特例。一般而言,二维矩阵为由行、列元素构成的矩阵表示;对于m行、n列的矩阵, 其大小为m×n。在MATLAB中表示矩阵与向量的方法很直观,下面举例说明
PS:公众号还不知道怎么编辑公式,只要部分截图,见谅
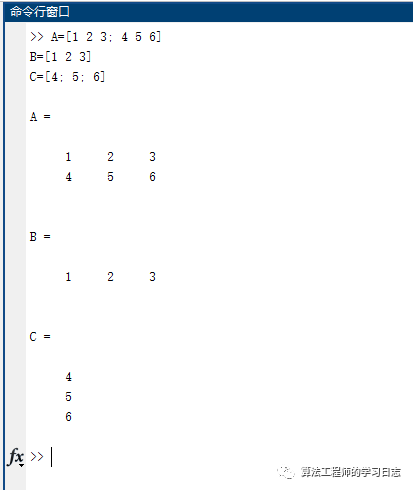
A=[1 2 3; 4 5 6]B=[1 2 3]C=[4; 5; 6]
注意:
(1) MATLAB中所有的矩阵与向量均包含在中括号[]之中。如果矩阵的大小为1×1,则它表示一个标量,如
>>a=3 %a表示一个数(2) 矩阵与向量中的元素可以为复数,在MATLAB中内置虚数单元为i、j;虚数的表达很直观,如3+4*i或者3+4*j 。
技巧:
(1) MATLAB中对矩阵或向量元素的引用方式与通常矩阵的引用方式一致,如A(2 ,3)表示矩阵A的第2行第3列的元素。如若对A的第2行第3列的元素重新赋值,只需键入如下命令:
>>A(2,3)=8;则矩阵A变为
A = 1 2 3 4 5 8(2) MATLAB中分号(;)的作用有两点:一是作为矩阵或向量的分行符,二是作为矩阵或向量的输出开关控制符。即如果输入矩阵或向量后键入分号,则矩阵与向量不在MATLAB命令窗口中显示,否则将在命令窗口中显示。如输入矩阵 、
>>A=[1 2 3; 4 5 6] % 按下Enter键则在 MATLAB命令窗口中显示
>>A = 1 2 3 4 5 6(3) 冒号操作符(:)的应用。冒号操作符在建立矩阵的索引与引用时非常方便且直接。如上述对多维矩阵F的建立中,冒号操作符表示对矩阵F第一维与第二维所有元素按照其顺序进行引用,从而对F进行快速赋值,无需一一赋值。如
>>B=2:5 %对向量进行赋值>>B= 2 3 4 5>>B(1:3)=2 %向量B从第1个到第3 个元素全部赋值为2>>B= 2 2 2 5>> C=6: -2:0 %将向量C进行递减赋值,初始值为6,终止值为0,步长为-2>>C= 6 4 2 0
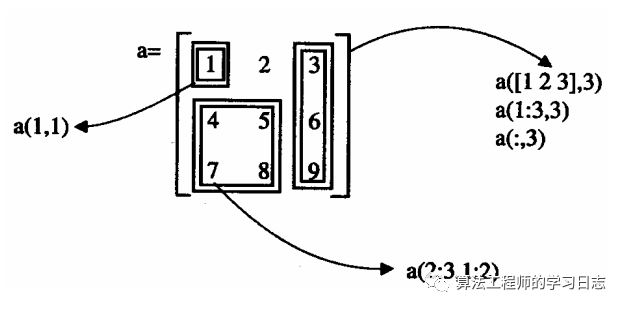
冒号操作符的使用很灵活,如图所示。
从图中可以看出,使用冒号操作符对矩阵元素进行引用非常灵活和方便,它可以有效地对矩阵的指定元素或指定区域进行各种操作与控制 。这使 得 MATLAB对矩阵的操作方式非常符合习惯的用法,易 于理解与应用。
2、MATLAB计算单元的基本操作
1. 矩阵加法与减法
如果矩阵A与矩阵B具有相同的维数,则可以定义矩阵的加法与减法,其结果为矩阵相应元素作运算所构成的矩阵。矩阵加法与减法在MATLAB中的表达方式为
>> C=A+B; %C为矩阵A与B之和>> D=A-B; %D为矩阵A与B之差
>>C=1 4 46 10 9>>D=1 0 22 0 3
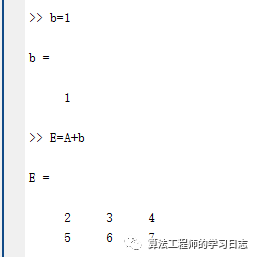
矩阵与标量的加法与减法是指标量本身与矩阵所有元素进行相应运算,如若b=1,E=A+b,则
>>E=2 3 45 6 7
2. 矩阵的乘法与除法
如果矩阵A的列数等于矩阵B的行数,则矩阵A、B可以相乘。其结果C=A*B在MATLAB中可表示为
>>C=A*B; %A、B相乘,若A、B不满足矩阵乘法法则,MATLAB会给出出错信息则
>>C=7 1116 29
如果矩阵A为方阵,A的p次方可以用A^p表示。如果p是一个正整数,那么这个幂可以由矩阵的连续相乘定义。当p=0时,其结果为与A相同的矩阵;当p<0时,只有在A的逆存在时才可定义 A^p ,其意义为inv(A)^(-p)。
在MATLAB中,矩阵除法有两种形式,即左除(\)和右除(/)。如果A是一个非奇异方阵,那么
>>A\B % 表示A的逆与B的左乘,即inv(A)*B>>B/A % 表示A的逆与B的右乘,即B* inv(A)
矩阵的左除和右除运算还可以用来求解矩阵方程
AX=B的解:
>>X=A\B如果A是一个方阵,X就是方程的解;如果A是一个行数大于列数的矩阵,X就是方程的最小二乘解。
3. 矩阵的转置
转置是一种重要的矩阵运算,在MATLAB中由撇号表示:
>> B=A' % B为A的转置如果A中含有复数元素,则A的转置矩阵中的元素为原来元素的共轭。
4. 对矩阵元素的操作与运算
在上述各种常用运算中,所有的操作都是针对矩阵所有元素或一部分元素的操作。其实还可以对矩阵元素进行单独的操作运算。对于加法和减法,对矩阵元素的操作与对矩阵的操作是一致的。其它运算对于所有矩阵元素的操作需要在操作符前加点
则
>>A.*B= % 矩阵对应元素相乘7 4-1 0>>B./A= % 矩阵对应元素相除7 1-1 0>>B.^2= % 矩阵元素乘方运算49 41 0>>A.^B= % 矩阵对应元素幂运算1 4-1 1>>C.'= % 矩阵转置1.0000+2.0000i,3.0000+1.0000i5.0000-2.0000i,1.0000+3.0000i