数据结构-排序

目录

前言

一、插入排序

1.直接插入排序

（1）算法实现

（2）图示理解

（3）算法分析

2.希尔排序

（1）算法实现

（2）图示理解

（3）算法分析

二、选择排序

1.选择排序

（1）算法实现

（2）图示理解

（3）算法分析

2.堆排序

（1）算法实现

（2）图示理解

（3）算法分析

三、交换排序

1.冒泡排序

（1）算法实现

（2）图示理解

（3）算法分析

2.快速排序

（1）算法实现

（2）图示理解

（3）算法分析

四、归并排序

1.归并排序

（1）算法实现

（2）图示理解

（3）算法分析

五、其它排序

1.计数排序

（1）算法实现

（2）图示理解

（3）算法分析

总结

---

---

前言

        生活中，很多时候我们都需要用到排序。例如，上体育课的时候，老师要求我们从矮到高排队；期末考试结束了，学校统计学生总分会按照分数高低排好名次；外卖软件会按照一定标准对商家进行排序，一般情况下我们会优先看到更好的商家/商品。数据结构中排序的概念基本如下：排序 ，就是重新排列表中的元素，使表中的元素满足按关键字有序的过程。

---

一、插入排序

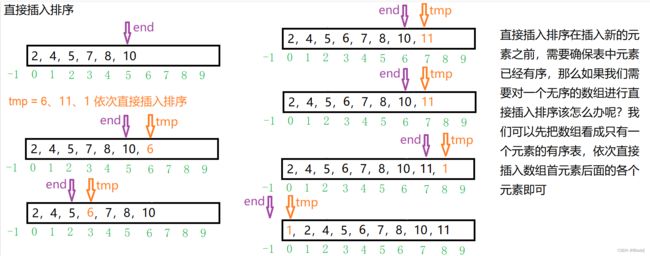
1.直接插入排序

（1）算法实现

void InsertSort(int* a, int n)
{
	for (int i = 1; i < n; i++)
	{
		int end = i - 1;
		int tmp = a[i];

		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}

		a[end + 1] = tmp;
	}
}

（2）图示理解

（3）算法分析

a.时间复杂度

时间复杂度（最坏）：O(N^2) -- 逆序
时间复杂度（最好）：O(N) -- 顺序有序

b.空间复杂度——O(1)

2.希尔排序

（1）算法实现

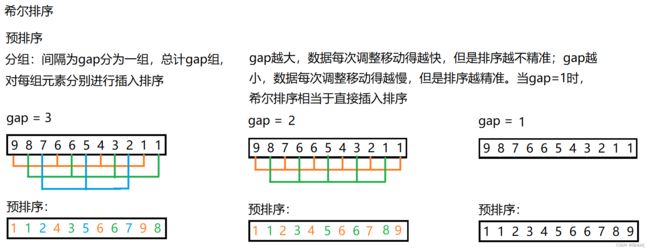
1.1 预排序 -- 接近有序（gap > 1）

        把表中的数据分为gap组，并对每组数据独立进行插入排序。注意：预排序是使表中的数据更接近有序，可能需要进行多次预排序，预排序可以使最后进行的插入排序调整的数据量更小。gap越大，数据每次调整移动得越快，但是排序越不精准；gap越小，数据每次调整移动得越慢，但是排序越精准。

1.2 插入排序（gap = 1）

        gap=1时，希尔排序与直接插入排序相同；

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;	//保证最后一次排序 gap = 1
		for (int i = 0; i < n - gap; i++)
		{
			int end = i, tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

（2）图示理解

（3）算法分析

a.时间复杂度（以gap = 3为例：）

希尔排序的时间复杂度的计算涉及到数学上的一些难题，在大量实验的基础上退出，它的时间复杂度约为O(N^1.3)

b.空间复杂度——O(1)

---

二、选择排序

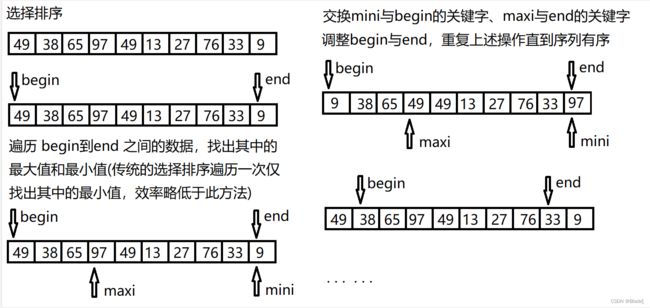
1.选择排序

（1）算法实现

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		// 记录待排序数据中的最大值和最小值
        int maxi = begin, mini = begin;
		for (int i = begin; i <= end; i++)
		{
			if (a[i] > a[maxi])
			{
				maxi = i;
			}

			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
        
		Swap(&a[begin], &a[mini]);
		// 如果maxi和begin重叠，修正一下即可
		if (begin == maxi)
		{
			maxi = mini;
		}

		Swap(&a[end], &a[maxi]);

		++begin;
		--end;
	}
}

（2）图示理解

（3）算法分析

a.时间复杂度——O(N^2)

b.空间复杂度——O(1)

c.稳定性——稳定

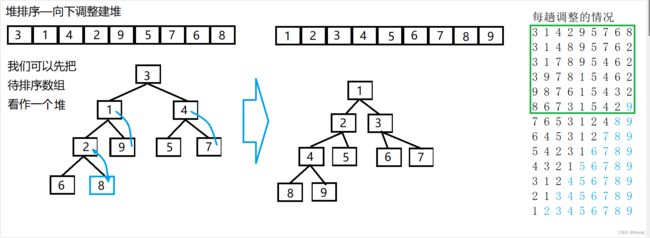
2.堆排序

（1）算法实现

void AdjustDwon(int* a, int n, int root)
{
	int child = root * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}

		if (a[child] > a[root])
		{
			Swap(&a[child], &a[root]);

			root = child;
			child = root * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDwon(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDwon(a, end, 0);

		end--;
	}
}

（2）图示理解

（3）算法分析

a.时间复杂度——O(N*logN(底数：2))

b.空间复杂度——O(1)

c.稳定性——不稳定

---

三、交换排序

1.冒泡排序

（1）算法实现

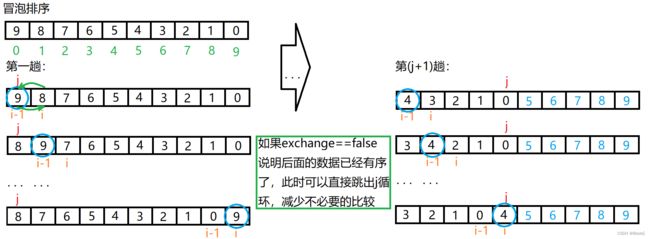
void BubbleSort(int* a, int n)
{
	for (int j = 0; j < n; ++j)
	{
		bool exchange = false;
		for (int i = 1; i < n - j; i++)
		{
			if (a[i - 1] > a[i])
			{
				int tmp = a[i];
				a[i] = a[i - 1];
				a[i - 1] = tmp;

				exchange = true;
			}
		}

		if (exchange == false)
		{
			break;
		}
	}
}

（2）图示理解

（3）算法分析

a.时间复杂度——O(N^2)

b.空间复杂度——O(1)

c.稳定性——稳定

2.快速排序

（1）算法实现

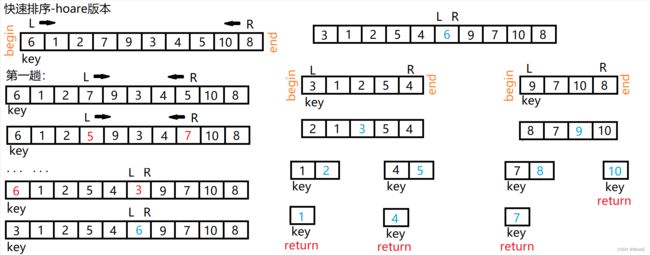
hoare版本

1.1 把最左端的数值的位置定为key，R先向左移动，找比key小的位置

1.2 L再向右移动，找比key大的位置

1.3 找到之后，交换R和L位置的数值

1.4 重复1.1~1.3的操作，直到R与L相遇

1.5 将R与L相遇的位置的数值与key位置的数值交换

1.6 此时原先key位置下的数值已经达到最终有序的位置了

1.7 这组数据被R与L相遇的位置分为两份，对每份数据再次进行上述操作

注意：如果把最左端的数值的位置定为key，就让右边的R先移动；如果把最右端的数值的位置定为key，就让左边的L先移动。以此来保证最后与key位置交换的数据是合理的

//[begin, end]
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	int left = begin, right = end;
	int keyi = left;
	while (left < right)
	{
		//left为key，右边先走
		//找小于key的数据
		while (left < right && a[right] >= a[keyi])
		{
			--right;
		}
		//找大于key的数据
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}

	Swap(&a[keyi], &a[left]);
	keyi = left;

	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}



//非递归（栈）
void QuickSortNonR(int* a, int begin, int end)
{
	ST st;
	STInit(&st);
	STPush(&st, end);
	STPush(&st, begin);

	while (!STEmpty(&st))
	{
		int left = STTop(&st);
		STPop(&st);

		int right = STTop(&st);
		STPop(&st);

		int keyi = PartSort3(a, left, right);
		//[begin, keyi-1]  keyi  [keyi+1, end]

		if (left < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, left);
		}

		if (keyi + 1 < right)
		{
			STPush(&st, right);
			STPush(&st, keyi + 1);
		}
	}

	STDestroy(&st);
}

（2）图示理解

（3）算法分析

a.平均时间复杂度——O(N*logN(底数：2))

   最坏的情况下（逆序）为O(N^2)

b.空间复杂度——O(N)

c.稳定性——不稳定

---

四、归并排序

1.归并排序

（1）算法实现

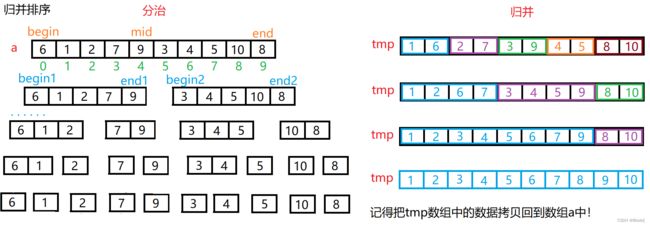
void MergeSortPart(int* a, int begin, int end, int* tmp)
{
	if (begin >= end) 
		return;

	int mid = (end + begin) / 2;

	//[begin, mid]  [mid+1, end]	分治递归，让子区间有序
	MergeSortPart(a, begin, mid, tmp);
	MergeSortPart(a, mid + 1, end, tmp);

	//归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin1;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	//我们不清楚[begin, mid]  [mid+1, end]哪一部分先结束
	//处理剩余的数据（理论上下面两个while循环只会执行一个）
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	//把归并的数据拷贝回原数组
	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail!\n");
		return;
	}

	MergeSortPart(a, 0, n - 1, tmp);

	free(tmp);
}



//非递归
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail!\n");
		return;
	}
	//
	int gap = 1;
	while (gap < n)
	{
		//printf("gap = %d -> ", gap);
		for (int i = 0; i < n; i += 2 * gap)
		{
			//[i, i+gap-1] [i+gap, i+2*gap-1]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//printf("[%d, %d] [%d, %d]--", begin1, end1, begin2, end2);

			//end1 或者 begin2越界，则可以不用归并了
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)	//只有end2越界了
			{
				end2 = n - 1;
			}

			int cnt = end2 - begin1 + 1;
			int j = begin1;
			//
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * cnt);
		}

		gap *= 2;
	}
	free(tmp);
}

（2）图示理解

（3）算法分析

a.时间复杂度——O(N*logN(底数：2))

b.空间复杂度——O(N)

c.稳定性——稳定

---

五、其它排序

1.计数排序

（1）算法实现

void CountSort(int* a, int n)
{
	int min = a[0], max = a[0];

	for (int i = 1; i < n; i++)
	{
		if (a[i] > max)
			max = a[i];
		if (a[i] < min)
			min = a[i];
	}

	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int) * range);
	if (count == NULL)
	{
		printf("malloc fail!\n");
		return;
	}

	memset(count, 0, sizeof(int) * range);
	//统计次数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}
	//回写排序
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		//出现几次，就回写 i + min
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}

（2）图示理解

（3）算法分析

a.平均时间复杂度——O(max(range, N))

b.空间复杂度——O(range)

c.稳定性——不稳定

---

总结