Seq2Seq和Attention机制详解

一、Seq2Seq简介

seq2seq模型最早可追溯到2014年的两篇paper [1, 2]，主要用于机器翻译任务（MT）。
seq2seq 是一个Encoder–Decoder 结构的网络，它的输入是一个序列，输出也是一个序列， Encoder 中将一个可变长度的信号序列变为固定长度的向量表达，Decoder 将这个固定长度的向量变成可变长度的目标的信号序列。
由于encoder与decoder两端处理的都是序列数据，所以被称为sequence-to-sequence，简称seq2seq。另外，目前应用最多的编/解码器是RNN（LSTM，GRU），但编/解码器并不限于RNN，如也有人拿MLP作为编码器。
paper[1, 2]的主要结构如下图：

Seq2Seq模型对于短文本的翻译来说效果很好，但是其也存在一定的缺点，如果文本稍长一些，就很容易丢失文本的一些信息，为了解决这个问题，Attention应运而生。

二、Seq2Seq with Attention

attention模型最早出现于cv领域，而首次用于解决nlp问题是在2014年[3]，seq2seq+attention 应用于机器翻译任务。以英译汉为例，当解码器对英文进行解码时，是一个词一个词生成的，而所生成的每个词对应的英文部分应该是不同，换句话说就是，解码器解码时不同step所分配的注意力是不同的。 再举一个例子，如看图说话（用一句话描述一幅图），所生成的词语应该对应图中的不同部分，即解码器在解码时，应该给图中“合适”的部位，分配更多的注意力（权重）。

paper[3]的主要结构如下图：

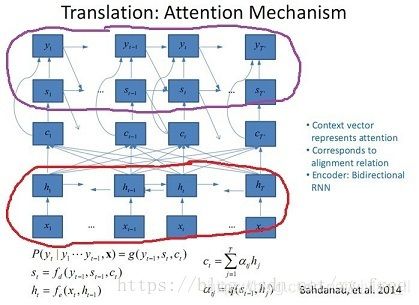
红圈标识的是编码器，其中h代表源文本的语义表示；紫圈标识的解码器，其中s代表目标文本的序列状态。c表示注意力向量，用来在解码时，控制源文本不同位置的attention分配。


（7）$p(y_t|y_{<t},x)=softmax(W_s{\hat{s}}_t)$，计算最后的输出概率。
（以上的步骤是luong在paper[4]里改良的decoder计算方式，paper[3]中在计算中加入了$c_t$}）

Attention扩展

luong在paper[4] 提出了一种attention改良方案，将attention划分为了两种形式：global， local.
global方式认为attention应该在所有源文本上进行，而local方式认为attention仅应该在部分源文本上进行。global理念与paper[3]相同，具体计算方式如下图所示：

其中“concat” 与 paper[3] 中的计算方式相同。
第一种：dot

输入是encoder的所有hidden states H: 大小为 (hid dim, sequence length) 。decoder在一个时间点上的hidden state， s： 大小为 （hid dim, 1） 。

第一步：旋转H为（sequence length, hid dim) 与s做点乘得到一个 大小为(sequence length, 1)的分数。

第二步：对分数做softmax得到一个合为1的权重。

第三步：将H与第二步得到的权重做点乘得到一个大小为(hid dim, 1)的context vector。

第二种：general

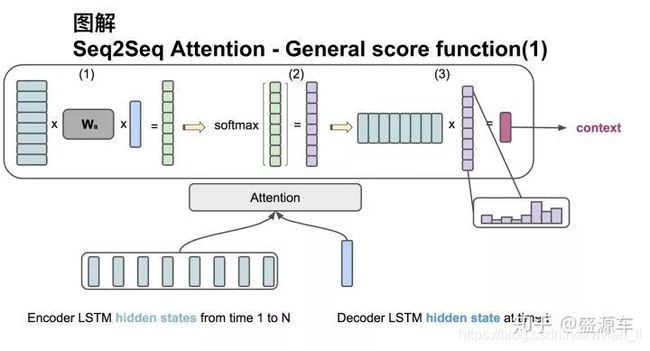
输入是encoder的所有hidden states H: 大小为 (hid dim1, sequence length) 。decoder在一个时间点上的hidden state， s： 大小为 （hid dim2, 1）。此处两个hidden state的纬度并不一样。

第一步：旋转H为（sequence length, hid dim1) 与 Wa 大小为[ hid dim1, hid dim 2)] 做点乘， 再和s做点乘得到一个 大小为(sequence length, 1)的分数。

第二步：对分数做softmax得到一个合为1的权重。

第三步：将H与第二步得到的权重做点乘得到一个大小为(hid dim, 1)的context vector。

需要注意的地方

• decoder 端的stst初始化：$s_0=tanh(W{h}_b^1)$, 取encoder的反向RNN的初态的非线性，作为decoder的初态
• teacher forcing模式与测试时（生成模式）不同，所以训练过程不能完全都用teacher forcing，teacher forcing 与 生成模式应按比例分配
• beamsearch 只是在测试的时候用到
• 如果encoder 与 decoder 的序列都很长，显存装不下。可考虑对decoder端进行截断，分步优化（pytorch中 使用 state = state.detach()）
• coding时，尽量别用for循环，会极大降低计算效率

总结

Attention与传统的Seq2Seq模型主要有以下两点不同：

• encoder提供了更多的数据给到decoder，encoder会把所有的节点的hidden state提供给decoder，而不仅仅只是encoder最后一个节点的hidden state 。
• decoder并不是直接把所有encoder提供的hidden state作为输入，而是采取一种选择机制，把最符合当前位置的hidden state选出来，具体的步骤如下：
  • 确定哪一个hidden state与当前节点关系最为密切；
  • 计算每一个hidden state的分数值；
  • 对每个分数值做一个softmax的计算，这能让相关性高的hidden state的分数值更大，相关性低的hidden state的分数值更低。

计算细节汇总如下：
$p(y_t|y<t,x)=softmax(W_s{\hat{s}}_t)$
${\hat{s}}_t=tanh(W_c[c_t;s_t])$
$s_t=f_d(y_{t-1},s_{t-1})$
$c_t=\sum {\alpha }_{tj}{h}_j$
${\alpha }_{ij}=softmax(e_{ij})$
$e_{tj}=a(s_{t-1},h_j)=v_a^{T}tanh(W{s}_{t-1}+U{h}_j)$
$h_t=f_e(x_t,ht-1)$ 注：$f_e$ 可使用LSTM， GRu， Bi-LSTM 等

参考文献：

[1] Sutskever I, Vinyals O, Le Q V. Sequence to sequence learning with neural networks[C]//Advances in neural information processing systems. 2014.
[2] Cho K, Van Merriënboer B, Gulcehre C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[J]. arXiv, 2014.
[3] Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate[J]. arXiv, 2014. & ICLR, 2015.
[4] Luong M T, Pham H, Manning C D. Effective approaches to attention-based neural machine translation[J]. arXiv, 2015.

参考网址：

真正的完全图解Seq2Seq Attention模型（非常好）
seq2seq + attention 详解（非常好）
Attention机制详解（有动图）
【机器学习】【seq2seq模型与attention机制，Beam Search】
【论文笔记】Effective Approaches to Attention-based Neural Machine Translation