02调制+滤波器+冲激函数的傅立叶变换

目录

一、调制方式

1.1 什么是调制？

1.2 为什么要调制？

1.3 如何调制？

1.4 调制包含的信号类型？

1. 消息信号

2. 载波信号

3. 调制信号

1.5 调制类型？

1. 调幅

2. 调频

3. 调相

4. 模拟脉冲调制

5. 脉冲编码调制

1.6 扩频？

1.直接序列扩频（DSSS)

2.跳频扩频技术（FHSS)

3.时跳变扩频技术（THSS)

二、滤波器分类

三、滤波器功能

四、有源滤波器的分析过程和方法

五、冲激函数

---

一、调制方式

1.1 什么是调制？

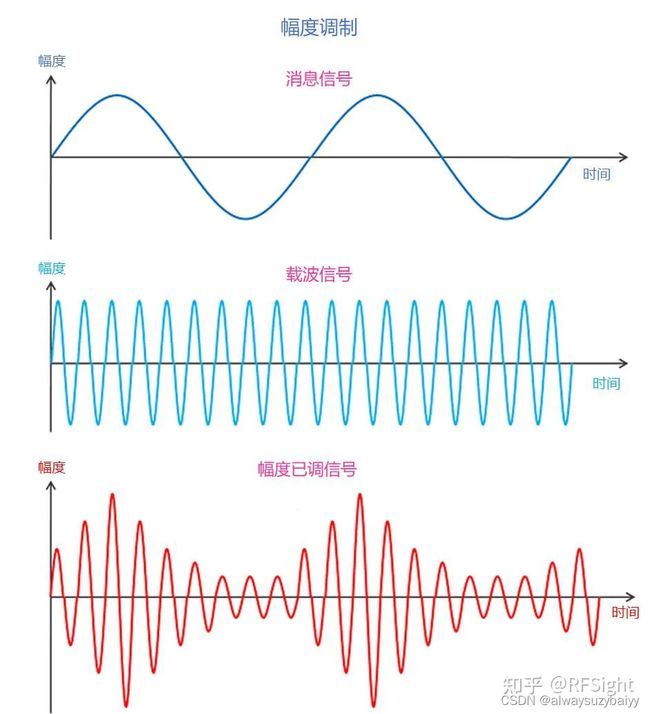
调制是将能量低的消息信号与能量高的载波信号进行混合，产生一个新的高能量信号的过程，该信号可以将信息传输到很远的距离。或者说，调制是根据消息信号的幅度去改变载波信号的特性（幅度、频率或者相位）的过程。下面我们通过一个简单的例子更深入的认识一下调制过程，如下图所示为幅度调制。

1.2 为什么要调制？

为了把消息信号传输到很远很远的地方，我们该怎么办呢？此时就通过高频率和高能量的载波信号来帮助我们实现，它传播距离更远，不容易受外部干扰的影响，这种高能量或高频信号称为载波信号。 

1.3 如何调制？

一个信号包括了幅度、频率和相位，那么我们可以根据消息信号的幅度来改变载波信号的幅度、频率和相位，即我们所熟知的调幅、调频和调相。

在调制过程中，载波信号的特性会根据调制方式发生变化，但是我们要传输的消息信号的特性是不会发生改变。

1.4 调制包含的信号类型？

1. 消息信号

消息信号就是我们要传播到目的地的消息，如我们的语音信号等，它也称调制信号或者基带信号。

2. 载波信号

具有振幅、频率和相位等特性，但是不包含任何有用信息的高能量或高频信号，我们称之为载波信号或载波

3. 调制信号

当消息信号与载波信号进行混合，会产生一个新的信号，我们称这个新信号为调制信号。

1.5 调制类型？

调制一般可分为：

模拟调制：指模拟消息信号直接调制在载波上，让载波的特性跟随其幅度进行变化。

数字调制：指调制信号或者消息信号已经不在是模拟形式，而是进行了模数转换，将数字基带信号调制到载波上进行传输，它的优点有高抗噪性、高可用带宽和容许功率。

1. 调幅

载波信号的幅度根据消息信号的幅度而变化（改变），而载波信号的频率和相位保持恒定。

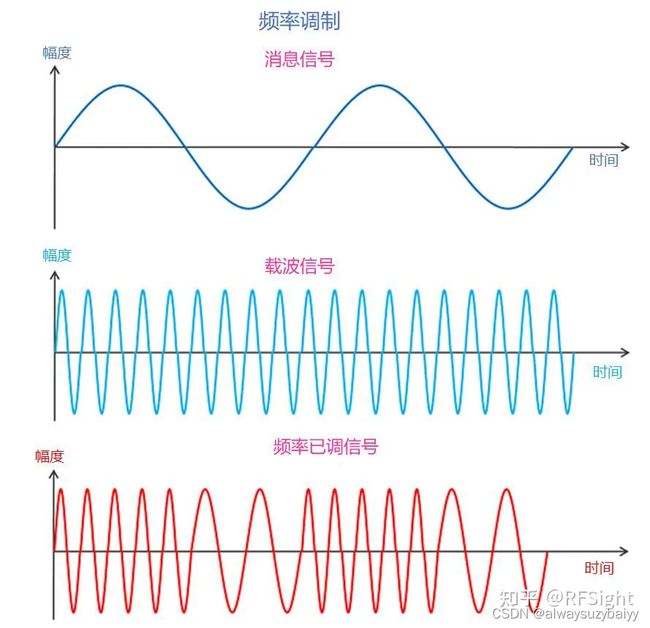
2. 调频

载波信号的频率根据消息信号的幅度而变化（改变），而载波信号的幅度和相位保持恒定。

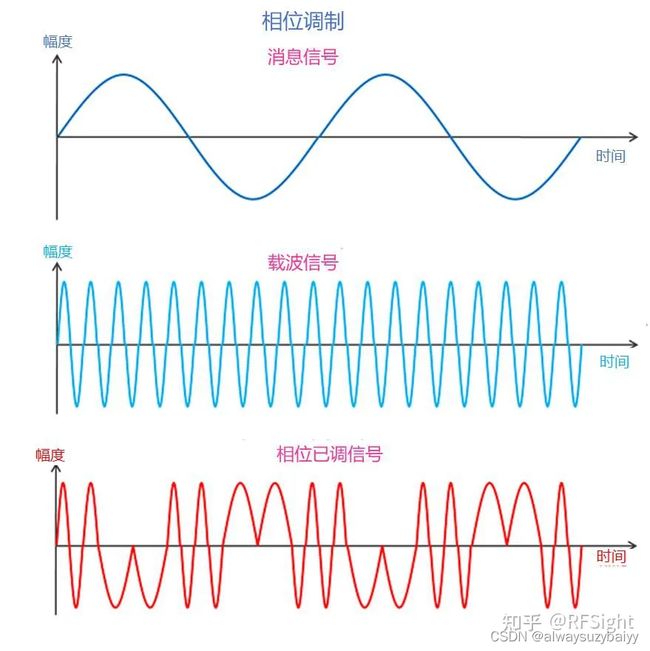
3. 调相

载波信号的相位根据消息信号的幅度而变化（改变），而载波信号的幅度保持恒定。

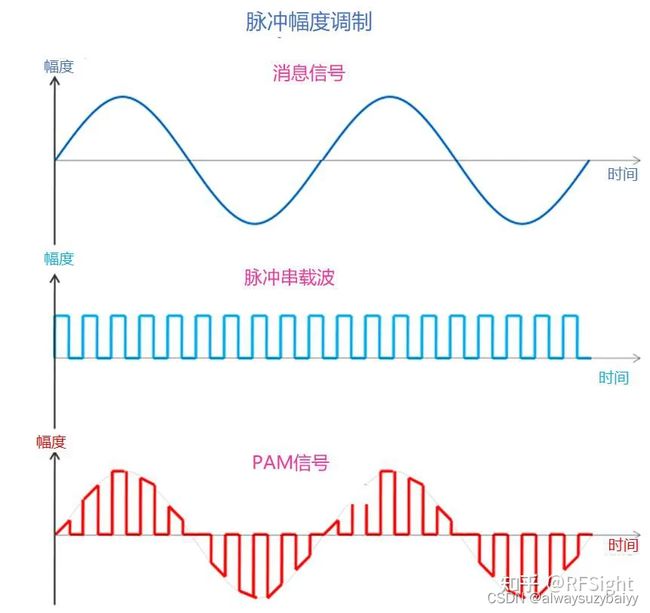
4. 模拟脉冲调制

根据消息信号的幅度改变载波脉冲的特性（脉冲幅度，脉冲宽度或脉冲位置）的过程。

5. 脉冲编码调制

是对连续变化的模拟信号进行抽样、量化和编码产生的数字信号。PCM的优点就是音质好，缺点就是体积大。

---

1.6 扩频？

1.直接序列扩频（DSSS)

如果在数据上直接注入扩频码，则可得到直序扩频（DSSS），在实际应用中，扩频码与通信信号相乘，产生完全被伪随机码“打乱”了的数据。在这种技术中，伪随机码直接加入载波调制器的数据上。调制器具有更大的比特率。用这样一个码序列调制射频载波的结果是产生一个中心在载波频率、频谱为（（sinx)/x)2的直序调制扩展频谱。

2.跳频扩频技术（FHSS)

如果扩频码作用在载波频率上，我们就得到跳频扩频（FHSS）。FHSS伪随机码使载波按照伪随机序列改变或跳变。顾名思义，FHSS中载波在一个很宽的频带上按照伪随机码的定义从一个频率跳变到另一个频率。

3.时跳变扩频技术（THSS)

如果用扩频码控制发射信号的开或关，则可得到时间跳变的扩频技术（THSS）。时跳变扩频技术利用伪随机序列控制功放的通/断，该项技术目前应用不多。

---

二、滤波器分类

按所处理的信号分为模拟滤波器和数字滤波器两种。

按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。

1、低通滤波器：它允许信号中的低频或直流分量通过，抑制高频分量或干扰和噪声；

2、高通滤波器：它允许信号中的高频分量通过，抑制低频或直流分量；

3、带通滤波器：它允许一定频段的信号通过，抑制低于或高于该频段的信号、干扰和噪声；

4、带阻滤波器：它抑制一定频段内的信号，允许该频段以外的信号通过。

按所采用的元器件分为无源和有源滤波器、陶瓷滤波器、晶体滤波器、机械滤波器、锁相环滤波器、开关电容滤波器等。

按通频带分类，有源滤波器可分为：低通滤波器（LPF）、高通滤波器（HPF）、带通滤波器（BPF）、带阻滤波器（BEF）等。

按通带滤波特性分类，有源滤波器可分为：最大平坦型（巴特沃思型）滤波器、等波纹型（切比雪夫型）滤波器、线性相移型（贝塞尔型）滤波器等。

按运放电路的构成分类，有源滤波器可分为：无限增益单反馈环型滤波器、无限增益多反馈环型滤波器、压控电源型滤波器、负阻变换器型滤波器、回转器型滤波器等。

除此之外，还有一些特殊滤波器，如满足一定频响特性、相移特性的特殊滤波器，例如，线性相移滤波器、时延滤波器、音响中的计杈网络滤波器、电视机中的中放声表面波滤波器等。

---

三、滤波器功能

电路功能：让某一频段的信号顺利通过，滤除其它频段的信号，所以它实际上是一种选频电路。

在微弱信号测量中，滤波器是一个非常重要的电路，模拟滤波器几乎在各种信号处理中必不可少。

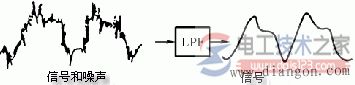
下图中信号是经过低通滤波器后的情况。

经过低通滤波器的处理，大大地提高了电路中的信/噪比。

---

四、有源滤波器的分析过程和方法

利用电路原理中的节点电流法→电压增益的传递函数→s用代入求增益的复数表达式→画出频率特性→求滤波电路的各项指标：通带增益、滤波器的截止频率(中心频率)、品质因素、带宽等。

---

五、冲激函数

应用：

冲激函数可用于信号处理，通过冲激函数来表示复杂的信号，可以简化对复杂信号的一些特性的研究。冲激函数及其延时冲激函数的线性组合来表示或逼近，再利用系统的迭加原理，可以通过简单的信号如单位冲激函数的频谱，以及频域特性来讨论比较复杂信号的频谱。从而减少计算复杂信号频谱的难度。