二叉树OJ练习题

检查两棵树是否相同

两种不同：结构上（一个为空，一个不为空。就结构不同），值上不同
第一步：判断结构；1：一个为空，一个不为空。2：两个都为空 3： 其它情况，就是都不为空

     //判断两棵树是否相同
        public boolean isSameTree(TreeNode p, TreeNode q) {
            if (p == null && q != null || p != null && q == null) {

                return false;

            }
            if (p == null && q == null) {

                return true;
            }
            if (p.val != q.val) {
                return false;
            }
            return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
        }

题目链接

找子树

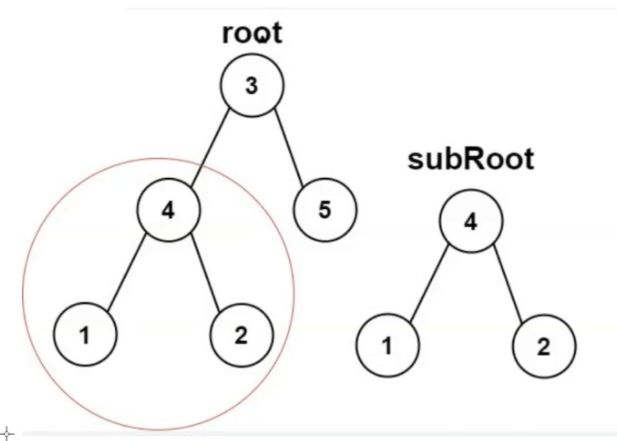
先判断是不是根节点的子树，然后走到左子树，左子树没有，走到右子树（可以利用到上一个代码的判断两棵树是否相同的代码）。每一个节点你都当成是一棵树去判断

public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p == null && q != null  || p != null && q == null ) {
            return false;
        }
        if(p == null && q == null) {
            return true;
        }
        if(p.val != q.val) {
            return false;
        }
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }

    //时间复杂度：root：r个节点     subRoot：有s个节点
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null ) return false;
        //1、判断两棵树 是不是两颗相同的树
        if(isSameTree(root,subRoot)) return true;         //第一行的判断，只能判断树是否为空。反正你走下去，我们判断函数
                                                          //会自己判断返回ture false，不需要你返回。。
                                                          //这个只判断传进来的根节点是否是空，是空就直接不可能相等
        //2、subRoot是不是 root.left 子树
        if(isSubtree(root.left,subRoot)) return true;
        //3、subRoot是不是 root.right 子树
        if(isSubtree(root.right,subRoot)) return true;
        return false;
    }

题目链接

反转二叉树

反转：左和右边的树交换位置，左边的子树左右又交换，右边也交换。
注意：交换节点和交换值是不同，交换节点是把这个节点为根节点的树就换过去了

public void reverseOddLevels(TreeNode root){
  if（root!=null）{
    Treenode tmp=root.left
    root.left=root.right
    root.right=tmp;
    reverseOddLevels(root.left)//递归左树
    reverseOddLevels(root.right)//递归右树
    return root；//应该这样子
}
return null;
}

判断是否平衡二叉树

什么是平衡二叉树？左右高度差小于等于1。
怎么判断：满足每棵子树必须是平衡二叉树；先判断左；再判断右

这个做法；时间复杂度是O(n^2)

时间复杂度O(n)

   public boolean isBalanced(TreeNode root) {
         if(root == null)  return true; 
            return maxDepth2(root) >= 0; 
    }
            //判断是否平衡二叉树
        public int maxDepth2(TreeNode root) {
            if(root == null) {
                return 0;
            }
            int leftHeight = maxDepth2(root.left);//
            int rightHeight = maxDepth2(root.right);//
            if(leftHeight >= 0 && rightHeight >= 0 &&
                    Math.abs(leftHeight-rightHeight) <= 1) { //这个是数学函数的方法；
                return Math.max(leftHeight,rightHeight) + 1;
            }else {
                return -1;
            }
        }//abs求绝对值，max求最大值。倒着比较和求。先最后一棵树看是否，平衡。
        //然后返回这棵树的大的高度给它的父亲。再和他父亲的右节点比较是否大于2

题目链接

对称二叉树

伪代码：

if（一边为空，一边不为空情况）{
不对称，
}

if (都为空){
   就是对称一种情况
}
走到这里，两个都不为空，都有元素，判断相等leftTree.val!=rihght.val，就说明不对称

然后递归左边（左边等于右边）
递归右边（右边等于左边）

       //对称二叉树
        public boolean usSymetric(TreeNode root){
            if(root==null){
                return true;

            }
            return isSymmetricChild(root.left,root.right);



        }

        public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){
            if (leftTree==null&&rightTree!=null||leftTree!=null&&rightTree==null){
                return false;
            }
            if(leftTree==null&&rightTree==null){

                return true;
            }
            if(leftTree.val!=rightTree.val){
                return false;
            }
            return isSymmetricChild(leftTree.left,rightTree.right)&&isSymmetricChild(leftTree.right,rightTree.left);


        }

构建二叉树

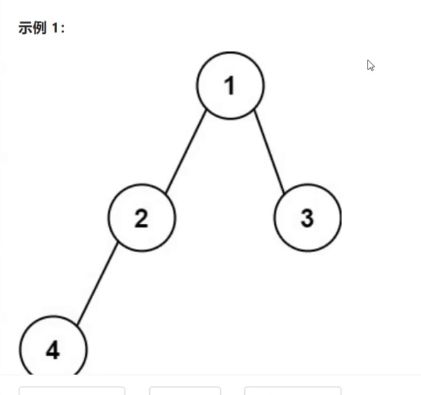
输入一个字符串；我们要构建成二叉树；并且中序遍历方式打印

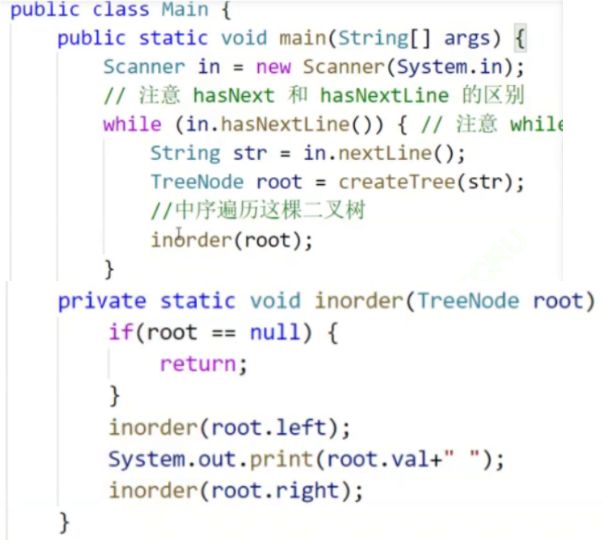
重点看一下怎么构建的：

       //构建二叉树
        public  int i=0;
        public TreeNode createTree(String str){
           TreeNode root=null;
           if(str.charAt(i)!='#'){
               root=new TreeNode(str.charAt(i));
               i++;
               root.left=createTree(str);
               root.right=createTree(str);
           }
           else {//空格#就不创建节点；i往下走
               i++;
           }
           return root;


        }

找最近公共祖先

题目：p！=q；p和q一定在树中；所有的值互不相同；注意这个前提

思路1：

牛逼的思想：如果反着来；孩子知道父亲；那是不是就好办些了。两个链表找它们的交点？

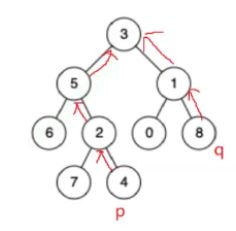
但是就是没有父亲节点的关系；父亲知道孩子；孩子不知道父亲。那你想到栈了吗？放到栈里面去;我们再按顺序取出节点时就是反过来的。
用两个栈：
第一个栈；存根节点到这个节点

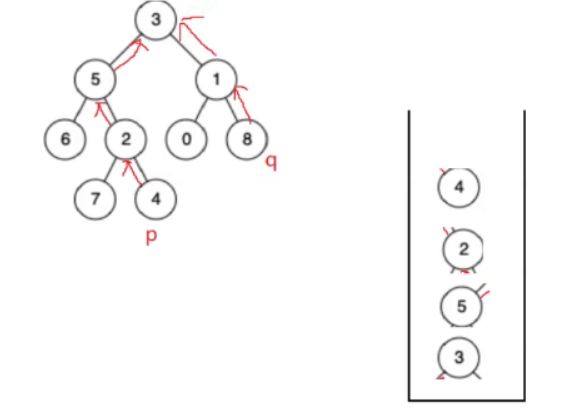
第二个栈：

现在对比两个栈之间的差值；然后再同时出栈。因为栈是最后进的先出；所以最下面突出来多余的就可以通过栈排除掉。然后它们就能在同一层；这样子才有机会是有公共祖先。

问题来了：如何储存根节点到指定路径的所有节点；我们怎么知道这个p在哪；在左边还是右边；是叶子节点还是中间节点？
那又是一个很牛逼的一个思想：
我们现在知道p这个节点。我从root开始往下递归；没找到p之前；我全部放进去。当我递归完左边（6的左右都为null）发现还没有找到p；那么我就去上一级的右边找（会退到5节点）；并且把这个节点（6节点）从栈踢出去。。。root==p就直接往回走结束。

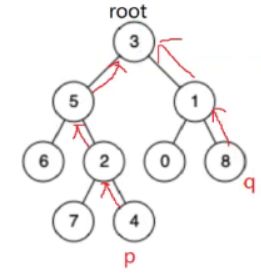
代码实现：

这个代码是把数据放入栈里


这里之所以形参能影响实参；因为这是引用类型；相当于传一个地址；它们操作的都是同一个对象

思路2：

源自于；二叉搜索树（根节点的左边都比根小；右边都比根大）；也叫二叉排序树；特点；中序遍历是有序的。
如果排好序；三种情况；要么有一个在根节点；要么都在左边/都在右边；要么一个在左边一个在右边

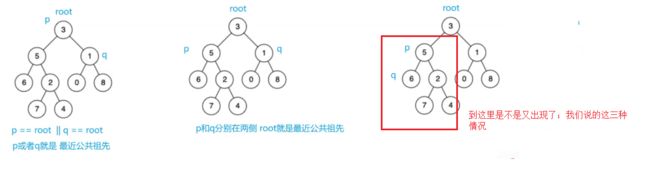
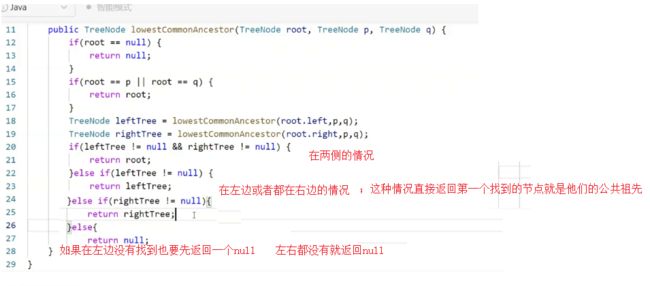
二叉搜索树转成双向链表

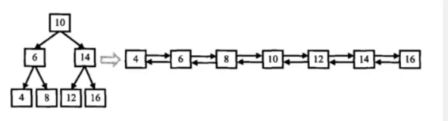
想一想这个东西和排好序的双向链表有什么关系：还是中序遍历；在合适的时机进行left和right的修改；最后返回1这个头节点

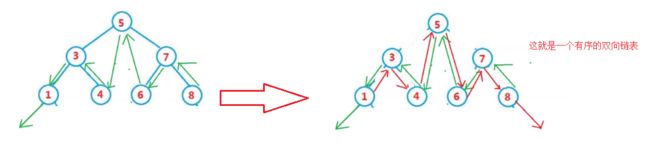
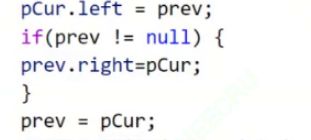
定义prev；这个节点的值是null；这样子就能给到1的左边。按下图这样子写；恰好能找到前驱的位置。在这中间还要多一步prev.reght=pCur;这就是双向链表节点的后继。注意：最开始prev=null时；你走perev.right就空指针异常。这个prev还不能在当前方法定义；不然每次递归下来都是定义的null


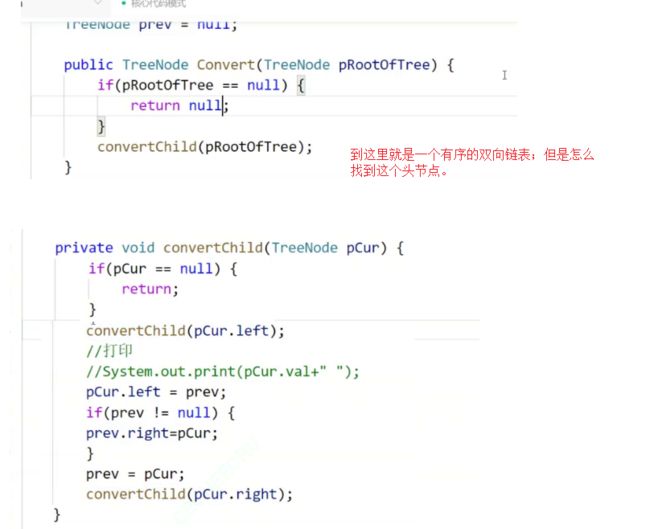
找头节点；利用传过去的根节点往前遍历；找到某一个的节点左边为空；那么这个就是头节点

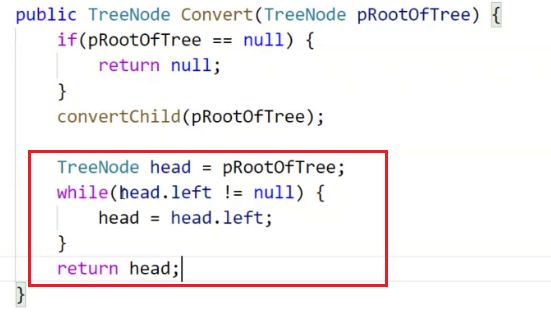
这三行代码可不简单啊：

非递归遍历二叉树

非递归前序遍历

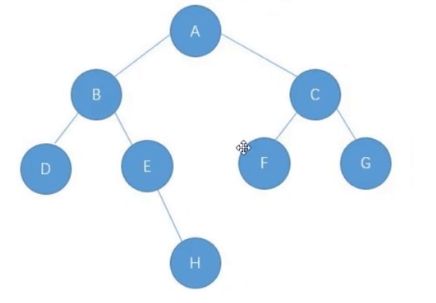
思路：使用栈；先把A放入栈（打印A）；再放B（打印B）；再放D（打印D）；当D的左边为null；出栈；并且把这个D记录下来；继续D的右边。反复之；模拟递归的过程

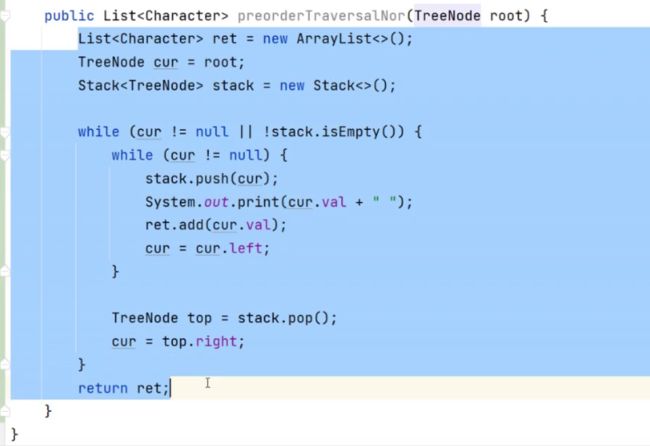
外面的循环是用来遍历右边的

非递归中序遍历

访问节点的时机不一样；打印的时机不一样；左边为空时才弹出打印。cur=null时；从栈里面弹元素；相当于递归的回归时候

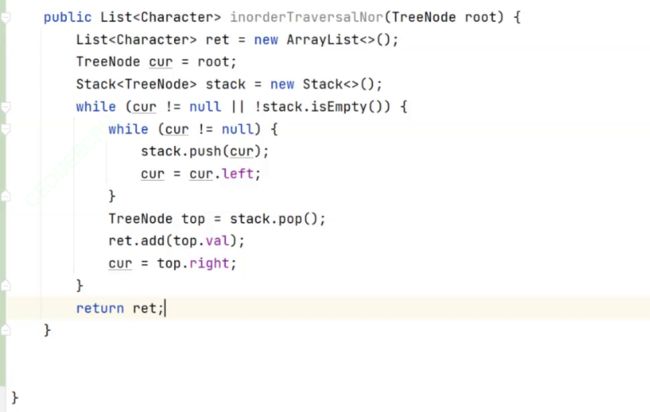
前序和后序；这个写代码的逻辑；外层循环是最后才写入的。

非递归后序遍历

不能先弹出栈的元素；我们瞄一眼；把右边的搞定后（如果右边没有东西就直接弹出打印）；再弹这个节点并且打印

根据前序和中序构建二叉树

根据中序和后序创建

先构建右子树；

preIndex要走到尾然后往回走


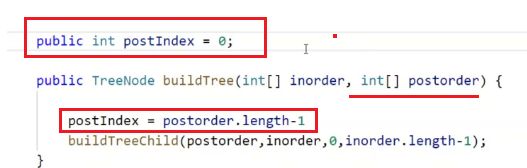
在前面前序和中序的代码修改这些部分即可

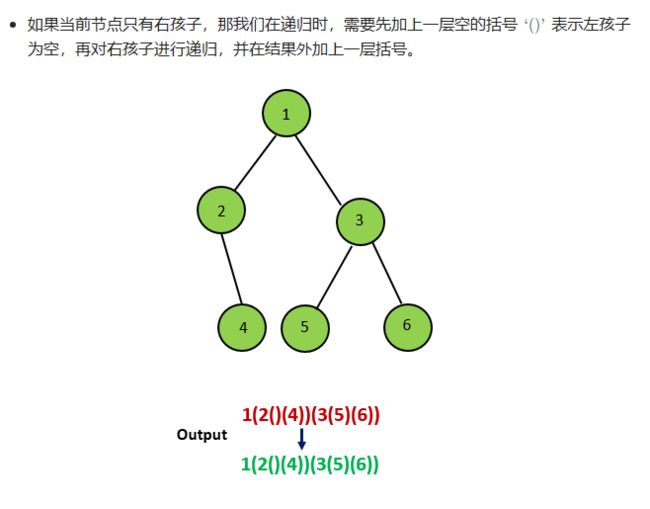
二叉树创建字符串

分四中情况：

class Solution {
    public String tree2str(TreeNode root) {
        if (root == null) {
            return "";
        }
        if (root.left == null && root.right == null) {
            return Integer.toString(root.val);
        }
        if (root.right == null) {
            return new StringBuffer().append(root.val).append((").append(tree2str(root.left)).append(")").toString();
        }
        return new StringBuffer().append(root.val).append("(").append(tree2str(root.left)).append("(").append(tree2str(root.right)).append(")").toString();
    }
}