Matlab(画图进阶)
目录
大纲
1.特殊的Plots
1.1 loglog(双对数刻度图)
1.3 plotyy(创建具有两个y轴的图形)
1.4yyaxis(创建具有两个y轴的图)
1.5 bar
3D条形图(bar3)
1.6 pie(饼图)
3D饼图
1.7 polar
2.Stairs And Ste阶梯图
3.Boxplot 箱型图和Error Bar误差条形图
3.1 boxplot
3.2 errorbar
4.fill(创建二维填充补片)
5.RGB颜色
6.imagesc(使用缩放颜色显示图像)
7.颜色条和方案
8.3D Plots
8.1.plot3
8.2 mesh()和surf()
8.3 contour()
8.4 meshc()和surfc()
9.view()视角
10.光线light():
11.patch()
在我们实际应用Matlab的过程中,往往还需要更加高难度的画图技术才可以满足我们的需求,高超的技术往往需要最朴实的手法,今天让我们一探究竟!!!
大纲
1.特殊的Plots
| loglog | 图与对数刻度为两个轴 |
| semilogx | x轴为对数刻度,y轴为线性刻度的图形 |
| semilogy | y轴为对数刻度,x轴为线性刻度的图形 |
| yyaxis | 左边和右边有y标记标签的图形 |
| hist | 直方图、柱形图 |
| bar | 条形图 |
| pie | 饼图 |
| polarlot | 极坐标图 |
1.1 loglog(双对数刻度图)
语法一:loglog(x,y) 在 x 轴和 y 轴上应用以 10 为底的对数刻度来绘制 x 和 y 坐标
- 要绘制由线段连接的一组坐标,将x和y指定为相同长度的向量
- 在同一组坐标区上绘制多组坐标,将x和y中的至少一个指定为矩阵
示例:
将
x定义为一个由区间 [10−1,102] 内的 50 个对数间距数组成的向量。将y定义为 2x。然后绘制x和y,并调用grid函数显示网格线
x = logspace(-1,2);%loglog默认就是以10为底的指数,所以这里只用定义上标数值便可
y = 2.^x;
loglog(x,y)
grid on 语法二:loglog(x1,y1,...,xn,yn) 在同一组坐标轴上绘制多对 x 和 y 坐标。此语法可替代将坐标指定为矩阵的形式。
示例:
创建一个由 x 坐标组成的向量和两个由 y 坐标组成的向量。通过将以逗号分隔的 x-y 对组传递给
loglog绘制两个线条。
x = logspace(-1,2);
y1 = 10.^x;
y2 = 1./10.^x;
loglog(x,y1,x,y2)
grid on 语法三:loglog(x,y,LineSpec) 使用指定的线型、标记和颜色创建绘图
示例:
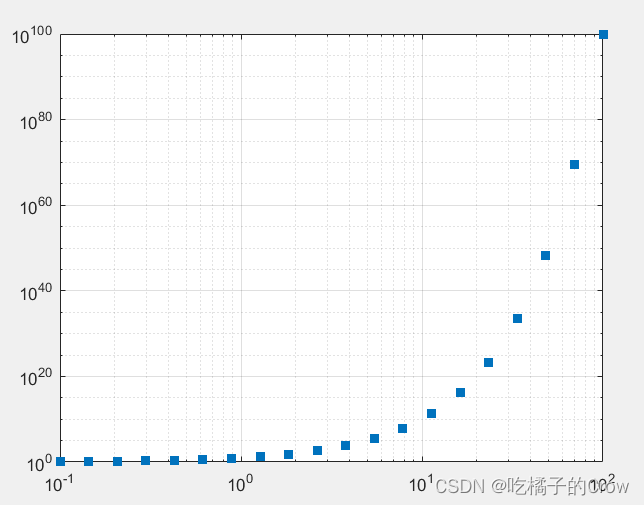
创建一组 x 坐标和 y 坐标,并将其显示在双对数图中。将线型指定为
's'以显示不带连接线的方形标记。将标记填充颜色指定为 RGB 三元组[0 0.447 0.741],它对应于深蓝色。
x = logspace(-1,2,20);
y = 10.^x;
loglog(x,y,'s','MarkerFaceColor',[0 0.447 0.741])
grid on语法一:semilogx(x,y) 在 x 轴上使用以 10 为底的对数刻度、在 y 轴上使用线性刻度来绘制 x 和 y 坐标。
-
要绘制由线段连接的一组坐标,请将
X和Y指定为相同长度的向量。 -
要在同一组坐标区上绘制多组坐标,请将
X或Y中的至少一个指定为矩阵。
示例:
将
x定义为一个由从0.1到100的对数间距值组成的向量,将y定义为x的副本。创建x和y的线性对数图,并调用grid函数显示网格线。
x = logspace(-1,2);
y = x;
semilogx(x,y)
grid on 语法二:semilogx(x1,y1,...,xn,yn) 在同一组坐标轴上绘制多对 x 和 y 坐标。此语法可替代将坐标指定为矩阵的形式
示例:
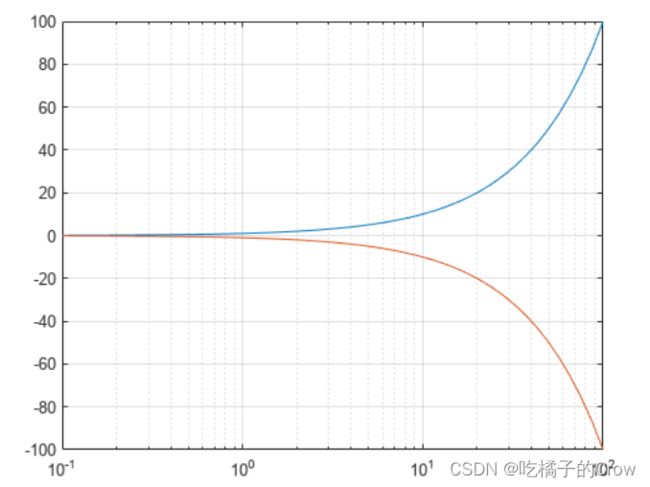
创建一个由对数间距 x 坐标组成的向量和两个由 y 坐标组成的向量。通过将以逗号分隔的 x-y 对组传递给
semilogx绘制两个线条。
%y = logspace(a,b) 生成一个由在 10^a 和 10^b(10 的 N 次幂)之间的 50 个对数间距点组成的行向量 y。logspace 函数对于创建频率向量特别有用。该函数是 linspace 和“:”运算符的对数等价函数。
x = logspace(-1,2);
y1 = x;
y2 = -x;
semilogx(x,y1,x,y2)
grid on 语法三:semilogx(x,y,LineSpec) 使用指定的线型、标记和颜色创建绘图。
示例:
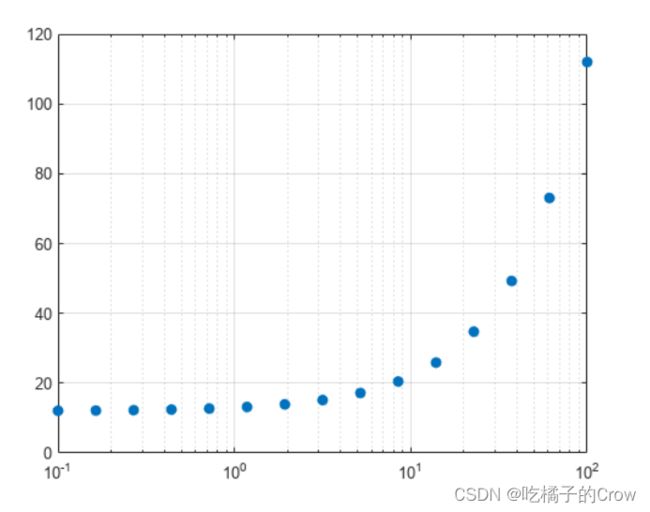
创建一组 x 坐标和 y 坐标,并将其显示在线性对数图中。将线型指定为
'o'以显示不带连接线的圆形标记。将标记填充颜色指定为 RGB 三元组[0 0.447 0.741],它对应于深蓝色。
%在10的幂10^-1和10^2之间生成15个点
x = logspace(-1,2,15);
y = 12 + x;
semilogx(x,y,'o','MarkerFaceColor',[0 0.447 0.741])
grid on不建议使用,有版本兼容问题
语法一:plotyy(X1,Y1,X2,Y2)绘制 Y1 对 X1 的图,在左侧显示 y 轴标签,并同时绘制 Y2 对 X2 的图,在右侧显示 y 轴标签。
示例:
- 使用两个不同的y轴在一个图上绘制两个数据集
x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x);
y2 = 0.8*exp(-0.5*x).*sin(10*x);
figure
plotyy(x,y1,x,y2)- 使用两个y轴在一个图上绘制两个数据集,添加标题和轴标签
x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x);
y2 = 0.8*exp(-0.5*x).*sin(10*x);
figure % new figure
%hAx是两个坐标轴的句柄,hLine1和hLine2分别是第一条曲线和第二条曲线的句柄
[hAx,hLine1,hLine2] = plotyy(x,y1,x,y2);
title('Multiple Decay Rates')
xlabel('Time (\musec)')
ylabel(hAx(1),'Slow Decay') % left y-axis
ylabel(hAx(2),'Fast Decay') % right y-axis1.4yyaxis(创建具有两个y轴的图)
语法一:yyaxis left 激活当前坐标区中与左侧 y 轴关联的一侧。后续图形命令的目标为左侧。如果当前坐标区中没有两个 y 轴,此命令将添加第二个 y 轴。如果没有坐标区,此命令将首先创建坐标区。
示例:
创建左右两侧都有 y 轴的坐标区。基于左侧 y 轴绘制一组数据的图。然后使用
yyaxis right激活右侧,使后续图形函数作用于该侧。基于右侧 y 轴绘制第二组数据的图,并为右侧 y 轴设置范围。
x = linspace(0,10);
y = sin(3*x);
yyaxis left
plot(x,y)
z = sin(3*x).*exp(0.5*x);
yyaxis right
plot(x,z)
ylim([-150 150])语法二:yyaxis right 激活当前坐标区中与右侧 y 轴关联的一侧。后续图形命令的目标为右侧。
语法三:yyaxis(ax,___) 指定 ax 坐标区(而不是当前坐标区)的活动侧。如果坐标区中没有两个 y 轴,此命令将添加第二个 y 轴。指定坐标区作为第一个输入参数。使用单引号将 'left' 和 'right' 引起来。
从R2019b开始,我们可以使用
tiledlayout和nexttile函数显示分块图。调用tiledlayout函数以创建一个 2×1 分块图布局。调用nexttile函数以创建坐标区对象ax1和ax2。通过指定ax1作为yyaxis的第一个输入,在顶部坐标区中添加第二个 y 轴。如果不指定坐标区,yyaxis将向当前坐标区添加第二个 y 轴。
>> colororder({'b','m'})%可以更改左右侧的颜色 b-蓝色 m-粉色
x = linspace(1,10);
tiledlayout(2,1)%创建一个2*1分块图布局
% Top plot
ax1 = nexttile;%调用函数nexttilt函数创建坐标区对象
yyaxis(ax1,'left')
plot(ax1,x,sin(x))
yyaxis(ax1,'right')
plot(ax1,x,exp(x))
% Bottom plot
ax2 = nexttile;
plot(ax2,1:10)1.5 bar
语法一:bar(y) 创建一个条形图,y 中的每个元素对应一个条形。
-
要绘制单个条形序列,请将
y指定为长度为 m 的向量。这些条形沿 x 轴从1到 m 依次放置。 -
要绘制多个条形序列,请将
y指定为矩阵,每个序列对应一列。
示例:
- 创建条形图
y = [75 91 105 123.5 131 150 179 203 226 249 281.5];
bar(y)- 指定沿x轴的条形位置
x = 1900:10:2000;
y = [75 91 105 123.5 131 150 179 203 226 249 281.5];
bar(x,y)- 指定条形宽度
y = [75 91 105 123.5 131 150 179 203 226 249 281.5];
bar(y,0.4)%将各条形的宽度设置为各条形可用总空间的 40%。- 显示条形组
y = [2 2 3; 2 5 6; 2 8 9; 2 11 12];%显示四个条形组,每一组包含三个条形。
bar(y)- 显示堆叠条形图
y = [2 2 3; 2 5 6; 2 8 9; 2 11 12];
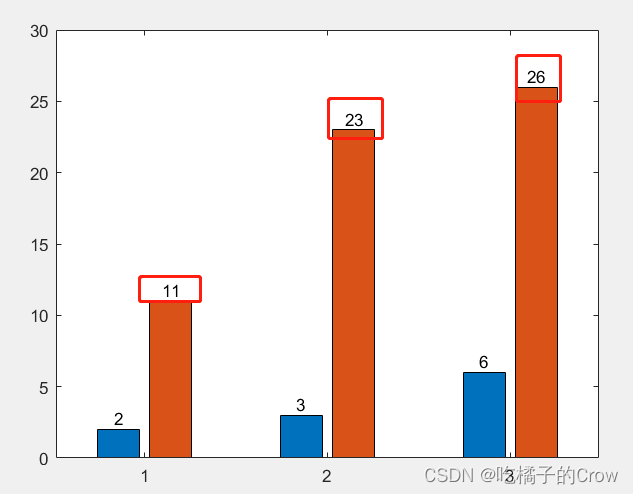
bar(y,'stacked')%为矩阵中的每一行显示一个条形。每个条形的高度是行中各元素之和。- 在条形末端指定标签
x = [1 2 3];
vals = [2 3 6; 11 23 26];
b = bar(x,vals);我们可以使得在条形序列的末端显示值,通过获得Bar对象的XEndPoints和YEndPoints属性,获取条形末端的坐标,将这些坐标传递给text函数,并指定垂直和水平对齐的方式,让值显示在条形末端上方居中处
xtips1 = b(1).XEndPoints;
ytips1 = b(1).YEndPoints;
labels1 = string(b(1).YData);
text(xtips1,ytips1,labels1,'HorizontalAlignment','center',...
'VerticalAlignment','bottom')xtips2 = b(2).XEndPoints;
ytips2 = b(2).YEndPoints;
labels2 = string(b(2).YData);
text(xtips2,ytips2,labels2,'HorizontalAlignment','center',...
'VerticalAlignment','bottom')-
3D条形图(bar3)
x = [1 2 5 4 8]; y = [x;1:5];
subplot(1,3,1); bar(x); title('A bargraph of vector x');
subplot(1,3,2); bar(y); title('A bargraph of vector y');
subplot(1,3,3); bar3(y); title('A 3D bargraph');1.6 pie(饼图)
语法一:pie(x) 使用 X 中的数据绘制饼图。饼图的每个扇区代表 X 中的一个元素。
-
如果
sum(X) ≤ 1,X中的值直接指定饼图扇区的面积。如果sum(X) < 1,pie仅绘制部分饼图。 -
如果
sum(X) > 1,则pie通过X/sum(X)对值进行归一化,以确定饼图的每个扇区的面积。 -
如果
X为categorical数据类型,则扇区对应于类别。每个扇区的面积是类别中的元素数除以X中的元素数的结果。
示例:
- 创建带偏移扇区的饼图
X = [1 3 0.5 2.5 2];
pie(X)%创建向量 X 的饼图。我们可以将对应的explode元素设置为1来偏移第二和第四块饼图扇区
explode = [0 1 0 1 0];
pie(X,explode)- 指定饼图的文本标签
X = 1:3;
labels = {'斗破','火影','海贼'};
pie(X,labels)- 修改饼图的文本标签
>> X = 1:3;
labels = {'斗破','火影','海贼'};
p=pie(X,labels)获取标签“Profit”的文本对象。更改其颜色和字体大小。使用圆点表示法设置属性。
t=p(6);
>> t.BackgroundColor='yellow';
>> t.EdgeColor='red';
>> t.FontSize=15
t =
Text (海贼) - 属性:
String: '海贼'
FontSize: 15
FontWeight: 'normal'
FontName: 'Helvetica'
Color: [0 0 0]
HorizontalAlignment: 'left'
Position: [1.1000 -2.6942e-16 0]
Units: 'data' 显示 所有属性 可修改属性
BackgroundColor: [1 1 0]
BeingDeleted: 'off'
BusyAction: 'queue'
ButtonDownFcn: ''
Children: [0×0 GraphicsPlaceholder]
Clipping: 'off'
Color: [0 0 0]
CreateFcn: ''
DeleteFcn: ''
EdgeColor: [1 0 0]
Editing: 'off'
Extent: [1.1000 -0.0897 0.2804 0.1794]
FontAngle: 'normal'
FontName: 'Helvetica'
FontSize: 15
FontSmoothing: 'on'
FontUnits: 'points'
FontWeight: 'normal'
HandleVisibility: 'on'
HitTest: 'on'
HorizontalAlignment: 'left'
Interpreter: 'tex'
Interruptible: 'on'
LineStyle: '-'
LineWidth: 0.5000
Margin: 3
Parent: [1×1 Axes]
PickableParts: 'visible'
Position: [1.1000 -2.6942e-16 0]
Rotation: 0
Selected: 'off'
SelectionHighlight: 'on'
String: '海贼'
Tag: ''
Type: 'text'
UIContextMenu: [0×0 GraphicsPlaceholder]
Units: 'data'
UserData: []
VerticalAlignment: 'middle'
Visible: 'on'- 指定百分比标签的格式
X = [1/3 2/3];
pie(X,'%.3f%%')%要在标签中包含百分号,请在表达式末尾指定 '%%'。-
3D饼图
>> X = 1:3;
labels = {'斗破','火影','海贼'};
pie3(X,labels)1.7 polar
%theta 弧度角 r 每个点的半径值
x = 1:100; theta = x/10; r = log10(x);
subplot(1,4,1); polar(theta,r);
theta = linspace(0, 2*pi); r = cos(4*theta);
subplot(1,4,2); polar(theta, r);
theta = linspace(0, 2*pi, 6); r = ones(1,length(theta));
subplot(1,4,3); polar(theta,r);
theta = linspace(0, 2*pi); r = 1-sin(theta);
subplot(1,4,4); polar(theta , r);2.Stairs And Ste阶梯图
| stair | 阶梯图 |
| stem | 绘制离散序列数据 |
x = linspace(0, 4*pi, 40); y = sin(x);
subplot(1,2,1); stairs(y);
subplot(1,2,2); stem(y);3.Boxplot 箱型图和Error Bar误差条形图
| boxplot | 用箱线图可视化汇总统计量 |
| errorbar | 含误差条的线图 |
3.1 boxplot
箱线图提供样本数据的汇总统计量的可视化,并包含以下特性:
-
每个箱子的底部和顶部分别表示样本的第 25 个和第 75 个百分位数。每个箱子的底部和顶部之间的距离表示四分位差。
-
每个箱子中间的红线表示样本中位数。如果中位数不在箱子的中心,则绘图显示样本偏度。
-
须线是自每个箱子的顶部向上延伸和底部向下延伸的线条。须线从四分位差的端点延伸到须线长度内最远的观测值(相邻值)。
-
超出须线长度的观测值标记为离群值。默认情况下,离群值是距离箱子底部或顶部超过 1.5 倍四分位差的值。不过,您可以通过使用额外的输入参数来调整此值。离群值显示为红色 + 号。
-
缺口显示样本间中位数的变异性。计算缺口的宽度,使得缺口不重叠的框在 5% 显著性水平上具有不同中位数。显著性水平基于正态分布假设,但对于其他分布,中位数比较也可合理地认为是稳健的。比较箱线图中位数就像目测假设检验,类似于用于均值的 t 检验。在某些情况下,缺口可能会延伸到箱子外部。
3.2 errorbar
errorbar(x,y,neg,pos) 在每个数据点处绘制一个垂直误差条,其中 neg 确定数据点下方的长度,pos 确定数据点上方的长度。
4.fill(创建二维填充补片)
语法一:fill(x,y,c) 将填充多边形区域绘制为补片,其顶点位于由 x 和 y 指定的 (x,y) 位置。
-
要绘制一个区域,请将
X和Y指定为向量。 -
要绘制多个区域,请将
X和Y指定为矩阵,其中每列对应一个多边形。
示例:
x = [0 4 5 2 1];
y = [0 0 2 4 3];
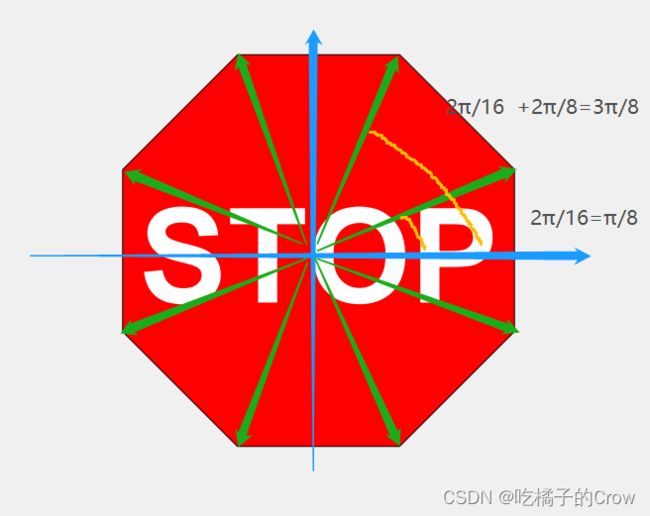
fill(x,y,'r')t =(1:2:15)'*pi/8; %关键算弧度
x = sin(t); y = cos(t);
fill(x,y,'r'); axis square off;
text(0,0,'STOP','Color', 'w', 'FontSize', 80, ...
'FontWeight','bold', 'HorizontalAlignment', 'center');练习:
5.RGB颜色
颜色自查表:
6.imagesc(使用缩放颜色显示图像)
语法一:imagesc(C) 将数组 C 中的数据显示为一个图像,该图像使用颜色图中的全部颜色。C 的每个元素指定图像的一个像素的颜色。生成的图像是一个 m×n 像素网格,其中 m 和 n 分别是 C 中的行数和列数。这些元素的行索引和列索引确定了对应像素的中心。
示例:
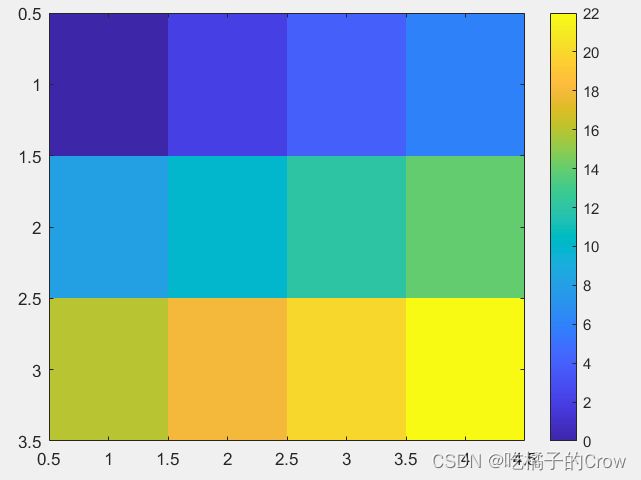
创建矩阵 C。显示 C 中数据的图像。向图添加颜色栏以显示当前颜色图。默认情况下,
imagesc色阶颜色范围以便图像使用颜色图中的所有颜色,其中C中的最小值映射到颜色图中的第一种颜色,最大值映射到最后一种颜色。
>> C = [0 2 4 6; 8 10 12 14; 16 18 20 22];
imagesc(C)
>> colorbar-
向三维视图的坐标区添加图像
Z = 10 + peaks;
surf(Z)
hold on
imagesc(Z) 语法二:imagesc(x,y,C) 指定图像位置。使用 x 和 y 可指定与 C(1,1) 和 C(m,n) 对应的边角的位置。要同时指定两个边角,请将 x 和 y 设置为二元素向量。要指定第一个边角并让 imagesc 确定另一个,请将 x 和 y 设为标量值。图像将根据需要进行拉伸和定向。
示例:
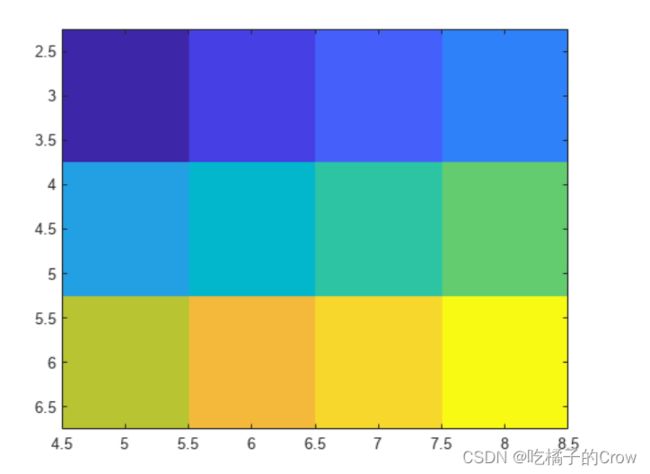
放置图像,使其位于 x 轴上的 5 和 8 之间及 y 轴上的 3 和 6 之间。
x = [5 8];
y = [3 6];
C = [0 2 4 6; 8 10 12 14; 16 18 20 22];
imagesc(x,y,C)注意:对应于 C(1,1) 的像素在点 (5,3) 上居中显示。对应于 C(3,4) 的像素在点 (8,6) 上居中显示。imagesc 在这两个点之间确定图像其余部分的位置和方向。
7.颜色条和方案
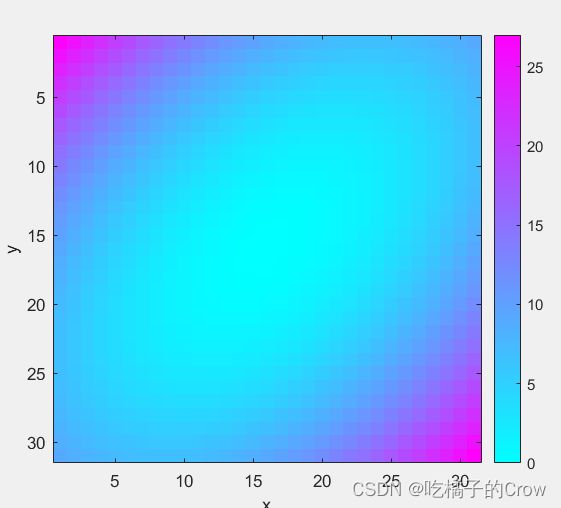
>> [x, y] = meshgrid(-3:.2:3,-3:.2:3);
z = x.^2 + x.*y + y.^2; surf( x, y, z); box on;
set(gca,'FontSize', 16); zlabel('z');
xlim([-4 4]); xlabel('x'); ylim([-4 4]); ylabel('y');
imagesc(z); axis square; xlabel('x'); ylabel('y');
>> colorbar
>> colormap(hot); colormap(cool);colormap(spring);颜色总表:
8.3D Plots
| plot3 | 三维线图像 |  |
| surf | 三维阴影曲面图 |  |
| surfc | 三维阴影表面下的轮廓图 |  |
| surface | 创建表面对象 | |
| meshc | 在网格图下绘制等值线图 |  |
| contour | 矩阵等高线图 |  |
| contourf | 填充了二维等高线图 |  |
如何将2维平面用3D视角观看:
x=0:0.1:2*pi;
plot(x,sin(x));方法一:
方法二:
>> x=0:0.1:2*pi;
plot(x,sin(x));
>> rotate3d on8.1.plot3
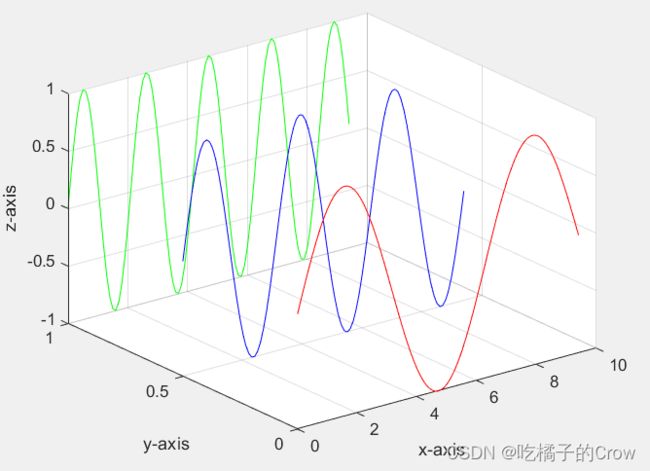
x=0:0.1:3*pi; z1=sin(x); z2=sin(2.*x); z3=sin(3.*x);
y1=zeros(size(x)); y3=ones(size(x)); y2=y3./2;
plot3(x,y1,z1,'r',x,y2,z2,'b',x,y3,z3,'g');
grid on;
xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis');三维曲面图原理:
- 通常用于绘图功能:Z=f(x,y)
- 需要为Matlab提供一组(x,y,z)点
x = -2:1:2;
y = -2:1:2;
[X,Y] = meshgrid(x,y)8.2 mesh()和surf()
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5;
[X,Y] = meshgrid(x,y);
Z = X.*exp(-X.^2-Y.^2);
subplot(1,2,1); mesh(X,Y,Z);
subplot(1,2,2); surf(X,Y,Z);8.3 contour()
x = -3.5:0.2:3.5;
y = -3.5:0.2:3.5;
[X,Y] = meshgrid(x,y);
Z = X.*exp(-X.^2-Y.^2);
subplot(2,1,1);
mesh(X,Y,Z);
axis square;
subplot(2,1,2);
contour(X,Y,Z);
axis square;各种等高线的表示:
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5;
[X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2);
subplot(1,3,1); contour(Z,[-.45:.05:.45]); axis square;
subplot(1,3,2); [C,h] = contour(Z);
clabel(C,h); axis square;
subplot(1,3,3); contourf(Z); axis square;8.4 meshc()和surfc()
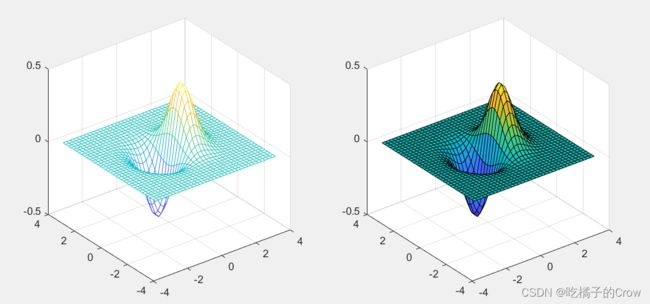
%比mesh()和surf()多了等高线
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5;
[X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2);
subplot(1,2,1); meshc(X,Y,Z);
subplot(1,2,2); surfc(X,Y,Z);9.view()视角
>> sphere(50); shading flat;
light('Position',[1 3 2]);
light('Position',[-3 -1 3]);
material shiny;
axis vis3d off;
set(gcf,'Color',[1 1 1]);
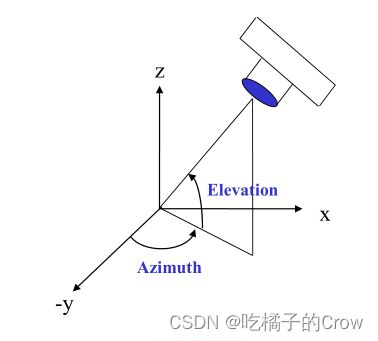
view(-45,20);10.光线light():
[X, Y, Z] = sphere(64); h = surf(X, Y, Z);
axis square vis3d off;
reds = zeros(256, 3); reds(:, 1) = (0:256.-1)/255;
colormap(reds); shading interp; lighting phong;
set(h, 'AmbientStrength', 0.75, 'DiffuseStrength', 0.5);
L1 = light('Position', [-1, -1, -1]);
set(L1, 'Position', [-1, -1, 1]);
set(L1, 'Color', 'g');11.patch()
v = [0 0 0; 1 0 0 ; 1 1 0; 0 1 0; 0.25 0.25 1; ...
0.75 0.25 1; 0.75 0.75 1; 0.25 0.75 1];
f = [1 2 3 4; 5 6 7 8; 1 2 6 5; 2 3 7 6; 3 4 8 7; 4 1 5 8];
subplot(1,2,1); patch('Vertices', v, 'Faces', f, ...
'FaceVertexCData', hsv(6), 'FaceColor', 'flat');
view(3); axis square tight; grid on;
subplot(1,2,2); patch('Vertices', v, 'Faces', f, ...
'FaceVertexCData', hsv(8), 'FaceColor', 'interp');
view(3); axis square tight; grid on;Matlab画图这方面确实是太强了,在我们游戏中有些图用Matlab也是可以画出来的,加油吧,少年!!!
load cape
X=conv2(ones(9,9)/81,cumsum(cumsum(randn(100,100)),2));
surf(X,'EdgeColor','none','EdgeLighting','Phong',...
'FaceColor','interp');
colormap(map); caxis([-10,300]);
grid off; axis off