查找（考研数据结构）
一、二叉查找树（BST）
1、BST的性质
【2011统考】下列关键字序列，不可能构成某二叉排序树中一条查找路径的是（A）
A、95，22，91，24，94，71 B、92，20，91，34，88，35
C、21，89，77，29，36，38 D、12，25，71，68，33，34
解析：
（95 22）：22~95
（95 22 91）：22~91
（95 22 91 24）：24~91
（95 22 91 24 94）：94不在范围内则不可能构成查找路径
tips：在区间内则逐步缩短区间范围，不在则非法。
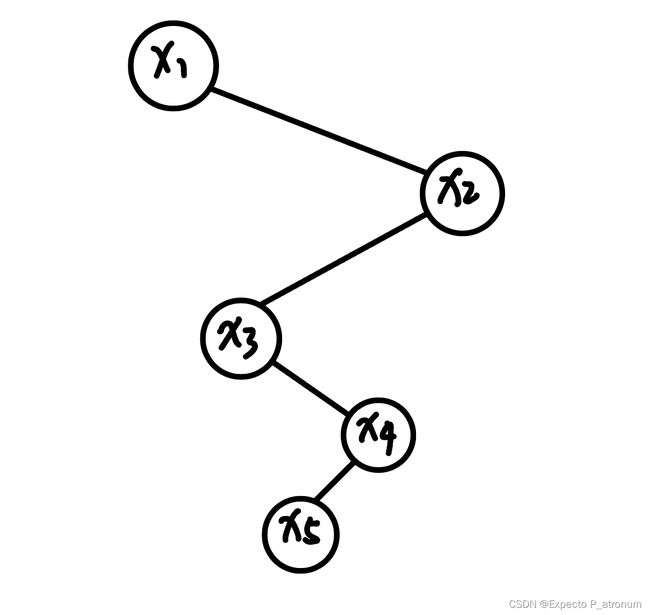
【2018统考】已知二叉排序树如下图，元素之间应满足的大小关系（C）
A、 x1 < x2 < x3 B、x1 < x4 < x5 C、x3 < x5 < x4 D、 x4 < x3
解析：右子树大于左子树，从图中看出 x1 < x3 < x5 < x4 < x2
2、BST的删除
【2013统考】在任意一颗非空二叉排序树T1中，删除某结点v之后形成二叉排序树T2，再将v插入T2形成二叉排序树T3.下列关于T1与T3的叙述中，正确的是（C）
（1）若v是T1的叶结点，则T1与T3不同
（2）若v是T1的叶结点，则T1与T3相同
（3）若v不是T1的叶结点，则T1与T3不同
（4）若v不是T1的叶结点，则T1与T3相同
A、（1）（3） B、（1）（4） C、（2）（3） D、（2）（4）
解析：
BST的删除若v是叶子结点，直接删；
若只有一棵子树，直接删除，用该子树代替v原来的位置；
若有两棵子树，则找到v的直接后继（或直接前驱），用该后继或前驱代替v，转换为删除该直接后继或前驱。
所以，叶子结点的删除不回改变原来树的结构，而非叶子结点会改变，而再插入则只会插入在叶子结点的位置，所以在非叶结点出删除插入必定会结构改变。
二、平衡二叉树
1、AVL的插入（旋转）
【2013统考】若将关键字1、2、3、4、5、6、7依次插入初始为空的平衡二叉树T，则T中平衡因子为0的分支结点的个数是（D）
A、0 B、1 C、2 D、3
解析：
AVL插入：
RR：A的右孩子的右子树插入 RL：A的右孩子的左子树插入
LL：A的左孩子的左子树插入 LR：A的左孩子的右子树插入
从失衡点的孩子开始旋转
三、顺序查找和折半查找
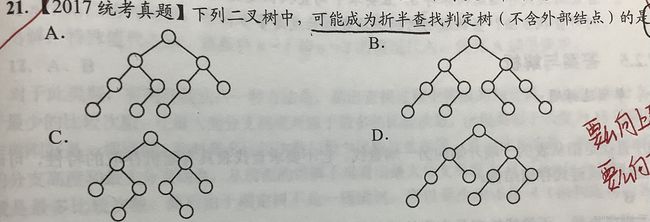
1、折半查找判定树
解析： 折半查找只能采取一种取整方式，向上取整或向下取整。
按1、2、3、4、5、6、7……填入A、B、C、D
2、折半查找算法
【2013统考】设包含4个数据元素的集合S={'do','for','repeat','while'}，各元素的查找概率依次为p1=0.35，p2=0.15，p3 = 0.15 ， p4 = 0.35。将S保存在一个长度为4的顺序表中，采用折半查找法，查找成功时的平均查找长度为2.2
1）若采用顺序存储结构保存S，且要求平均查找长度更短，则元素应如何排列？应使用何种查找方法？查找成功时平均查找长度是多少？
2）若采用链式结构保存S，且要求平均查找长度更短，则元素应如何排列？应使用何种查找方法？查找成功时的平均查找长度是多少？
1）按查找概率从大到小排序，顺序查找，ASL = 0.35 * 1 + 0.35 * 2+ 0.15 * 3 + 0.15 * 4 = 2.1
2）按照二叉排序树的方式（二叉链表）排序 或 采用顺序查找
采用链式存储只能采用顺序查找，当基本有序时，顺序查找可能会优于折半查找
四、B树和B+树
【2009统考】下列叙述中，不符合m阶B树定义要求的是（D）
A、根结点最多含有m棵子树 B、所有叶结点都在同一层上
C、各结点内关键字均升序或降序排列 D、叶结点之间通过指针链接
解析：
m阶B树性质：
1、每个结点至多含有m棵子树，即m-1个关键字
2、若根结点不是叶结点，则至少含有两颗子树
3、除根结点外所有非叶结点至少含有
棵子树，即至少含有
个关键字
通过指针链接的是B+树
【2014统考】在一棵有15个关键字的4阶B树中，含关键字的结点个数最多是（D）
A、5 B、6 C、10 D、15
解析：
4阶B树最多含有每个结点至少1个关键字，所以共15个关键字，15 / 1 = 15个关键字
【2016统考】B+树不同于B树的特点之一是（A）
A、能支持顺序查找 B、结点中含有关键字
C、根结点至少有两个分支 D、所有叶结点都在同一层上
解析：
B+树有两个头结点，一个指向最小的关键字，另一个指向根结点。
B树只有指向根结点的头结点。
从最小关键字开始，就可以实现顺序查找。
顺序查找：按照原序列的顺序查找
【2018统考】高度为5的3阶B树含有的关键字个数至少是（B）
A、15 B、31 C、62 D、242
解析：
3阶，每个结点关键字个数至少为1个，根结点的子树个数至少为2棵且每个结点关键字至少一个。
所以，此时关键字数 = 结点数，每棵子树有两个结点。类似于一颗满二叉树，一颗高度为n的满二叉树的结点数
。所以等于31.
【2022统考】在下图所示的5阶B树T中，删除关键字260之后需要进行必要的调整，得到新的B树T1.下列选项中，不可能是T1根结点中关键字序列的是（D）
A、60，90，280 B、60，90，350
C、60，85，110，350 D、60，90，110，350
解析：
*5阶B树至少
个关键字，删除260后，根结点仍然满足最小2个关键字。
需要调整结点的关键字。
*若将110移到根结点，则第三个结点只有1个关键字，不满足条件，所以D不可能。
B树的删除：
*删除后关键字的结点不能关键字数量不能小于
，若小于则要从兄弟借，若不够借则合并双亲结点和左（右）兄弟结点。
五、散列表
【2018统考】现有长度为7、初始为空对散列表HT，散列函数H(k) = k % 7，用线性探测再散列法解决冲突。将关键字22，43，15依次插入HT后，查找成功的平均查找长度是（C）
A、1.5 B、1.6 C、2 D、3
解析：
22 % 7 = 1
43 % 7 = 1 冲突，改为2
15 % 7 = 1 冲突，改为2冲突，改为3
查找22时，H(22) = 22 % 7 = 1，1次成功；查找43，H(43) = 43 % 7 = 1，+1 = 2，查找成功，两次；查找15，H(15) = 15 % 7 = 1，而15在3处，则需要查找3次。
ASL：（1 + 2 + 3） / 3 = 2
线性探测法：若有冲突则往后加一个单元探测，直到该存储单元为空。
【2019统考】现有长度为11且初始为空的散列表HT，散列函数是H（key） = key % 7，采用线性探测法。将关键字序列87，40，30，6，11，22，98，20依次插入HT后，HT查找失败的平均查找长度是（Ｃ）
A、4 B、5.25 C、6 D、6.29
解析：插入87，87 % 7 = 3；插入40，40 % 7 = 5 ；插入30，30 % 7 = 2；插入6，6 % 7 = 6；插入11，11 % 7 = 4；插入22，22 % 7 = 1；插入98，98 % 7 = 0 ；插入20，20 % 7 = 6，7合法
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 98 | 22 | 30 | 87 | 11 | 40 | 6 | 20 |
关键字为0，需要查找9次，从0号到8号；关键字为1，需要查找8次，从1～8……
ASL（失败） = （9 + 8 + 7 + 6 + 5 + 4+ 3 ）/ 7 = 6