DFS深搜算法(详解+例题)
DFS是英文Depth-First-Search的缩写,意思是深度优先搜索。
什么是深度优先搜索呢?顾名思义,就是往深处遍历。举个小例子:
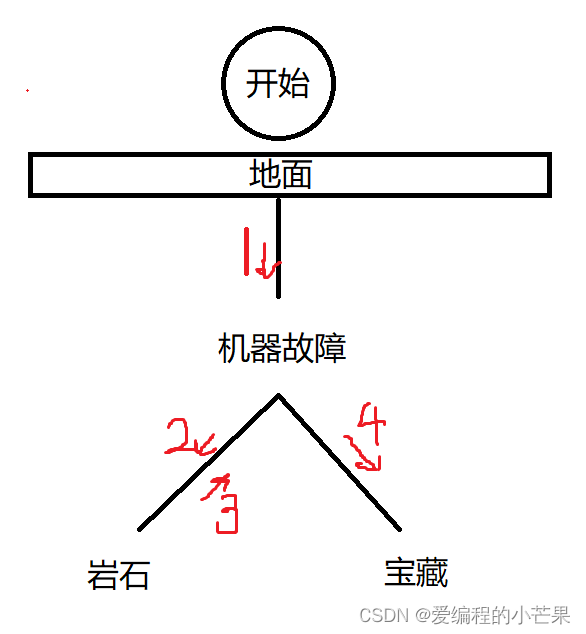
假设你现在要挖宝藏,你肯定会往下挖对吧。当你挖到地下10米时,探宝器出现了一个故障。一会儿显示往右下挖,一会儿显示往左下挖。你只好先往左下挖。挖啊挖,不幸的是你挖到了岩石,不能在往下挖了。你只好往回爬,爬到那个分叉口,这次你往右下挖,果然一路顺畅,挖到了宝藏!
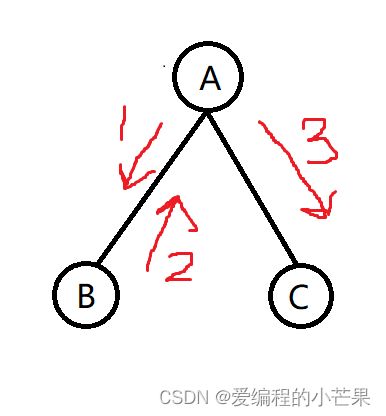
这是你挖宝的路线: 这是dfs的路线:
这下你应该懂dfs的含义了吧。
对了你爬回去的动作,在dfs里叫作回溯。
那dfs有没有框架呢?有是有的,不像贪心没什么框架(有兴趣的可以看一看我博客里的贪心算法讲解)
框架:
void dfs(需要啥参数自己定)
{
if(终止条件)
{
cout<<输出答案<话不多说,上例题,边看题边理解!
1、全排列问题(洛谷 P1706 C++)
我也有一篇博客是专门讲这道题的,但是那个要VIP,这篇不用,而且内容一样,还不快点个赞!
题目描述:
按照字典序输出自然数 1 到 n 所有不重复的排列,即 n 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
输入格式:
一个整数 n。
输出格式:
由 1∼n 组成的所有不重复的数字序列,每行一个序列。
每个数字保留 5个场宽。
输入输出样例:
输入:3
输出: 1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
思路:
这题是一道用dfs解决的经典问题。
我们可以这样想,有n个数,那么就会有n个空位要填进去数。
那么终止条件就应该是当已经填的空位数等于n时。
在dfs中,从1到n循环依次判断能否放入空位中。
1:若能,将此数存放置数组内并递归下一个空位,也就是dfs(x+1)。
2:若不能,则接着判断下一个数。
而此处的判断条件应该是此数是否出现过,因为全排列不能出现相同的数。
我们可以定一个vis[]数组来判断此数是否出现过(开始全部为false)。
判断时,只需看看这个位置的数组元素是true还是false。
如果是真执行‘思路’正数第四行,如果是假执行‘思路’正数第五行。
最后一定要记得把vis[]设为false(也就是回溯)!
参考代码:
#include
using namespace std;
bool vis[10];
int n,a[100];
void dfs(int k)
{
//当已经填好的空位数=n时,按格式输出a[i]并终止
if(k==n)
{
for(int i=1;i<=n;i++) cout<>n;
dfs(0);//表示已经填好的空位数
return 0;
} 2、自然数的拆分问题(洛谷 P2404 C++)
 思路点拨:
思路点拨:
看到这题,首先就会想到用深搜。对,这道题的正解的确是深搜。
可搜什么呢?假如你看到一道题给出的数字是5,让你拆分,你会怎么分呢?
相信大家的思路都是这样的:
首先确定第一个数字,从小的开始,也就是说第一个数字可以是1。
接下来,我们发现,1后面数字相加的和,只可能是5-1=4。
紧接着,我们把4来拆分,还是从1开始拆,那么现在的算式就变成了1+1。
那后面拆分的总和应该是5-2/4-1=3,以此类推,最终拆成1+1+1+1+1。
那如果第一个数拆2呢,那么剩下的数相加得5-2=3。
再把3拆分,最后得出结果。
这是我们人的思路,那程序怎么写呢?
我们可以dfs(cur,sum),表示当前考虑cur,还剩sum需要划分。
注意:在dfs里因该有两种情况,分别是选或不选。
最后奉上完整代码。
AC代码:
#include
using namespace std;
int n,t=0,a[10000];
void dfs(int cur,int sum)//考虑cur,还剩下sum需要划分
{
//当没有余下的(没有需要划分时),输出答案
if(sum==0)
{
cout<sum||cur==n) return;
a[t++]=cur;//把考虑的数加入答案数组
dfs(cur,sum-cur);//选cur
t--;//回溯
dfs(cur+1,sum);//不选cur
}
int main()
{
cin>>n;
dfs(1,n);
return 0;
} 你学会了吗?都看到这里了,还不给我一个免费的一键三连?
我还是一名小学生希望多多支持一下,谢谢!