2023年03月 C/C++（六级）真题解析#中国电子学会#全国青少年软件编程等级考试

C/C++编程（1~8级）全部真题・点这里

第1题：波兰表达式

波兰表达式是一种把运算符前置的算术表达式，例如普通的表达式2 + 3的波兰表示法为+ 2 3。波兰表达式的优点是运算符之间不必有优先级关系，也不必用括号改变运算次序，例如(2 + 3) * 4的波兰表示法为* + 2 3 4。本题求解波兰表达式的值，其中运算符包括+ - * /四个。
时间限制：1000
内存限制：65536
输入
输入为一行，其中运算符和运算数之间都用空格分隔，运算数是浮点数。
输出
输出为一行，表达式的值。 可直接用printf(“%f\n”, v)输出表达式的值v。
样例输入
* + 11.0 12.0 + 24.0 35.0
样例输出
1357.000000

下面是解决这个问题的C语言代码：

#include 
#include 
#include 
#include 

#define MAX_SIZE 100

// 定义栈结构
typedef struct {
    int top;
    double stack[MAX_SIZE];
} Stack;

// 初始化栈
void initialize(Stack *s) {
    s->top = -1;
}

// 判断栈是否为空
int isEmpty(Stack *s) {
    return s->top == -1;
}

// 判断栈是否已满
int isFull(Stack *s) {
    return s->top == MAX_SIZE - 1;
}

// 入栈
void push(Stack *s, double value) {
    if (isFull(s)) {
        printf("Stack is full. Cannot push element.\n");
    } else {
        s->stack[++(s->top)] = value;
    }
}

// 出栈
double pop(Stack *s) {
    if (isEmpty(s)) {
        printf("Stack is empty. Cannot pop element.\n");
        return 0.0;
    } else {
        return s->stack[(s->top)--];
    }
}

// 计算波兰表达式的值
double calculatePolishExpression(char *expression) {
    Stack stack;
    initialize(&stack);

    int len = strlen(expression);
    char *token = strtok(expression, " ");

    while (token != NULL) {
        // 如果是运算符，则弹出栈顶的两个元素进行运算，并将结果入栈
        if (strcmp(token, "+") == 0 || strcmp(token, "-") == 0 ||
            strcmp(token, "*") == 0 || strcmp(token, "/") == 0) {
            double operand2 = pop(&stack);
            double operand1 = pop(&stack);
            double result = 0.0;

            if (strcmp(token, "+") == 0) {
                result = operand1 + operand2;
            } else if (strcmp(token, "-") == 0) {
                result = operand1 - operand2;
            } else if (strcmp(token, "*") == 0) {
                result = operand1 * operand2;
            } else if (strcmp(token, "/") == 0) {
                result = operand1 / operand2;
            }

            push(&stack, result);
        }
        // 如果是运算数，则将其转换为浮点数并入栈
        else {
            double number = atof(token);
            push(&stack, number);
        }

        token = strtok(NULL, " ");
    }

    // 返回栈顶的元素，即为表达式的值
    return pop(&stack);
}

int main() {
    char expression[MAX_SIZE];
    fgets(expression, MAX_SIZE, stdin);

    // 删除末尾的换行符
    expression[strcspn(expression, "\n")] = '\0';

    double result = calculatePolishExpression(expression);

    printf("%f\n", result);

    return 0;
}

该程序首先定义了一个栈的结构体，并实现了栈的相关操作函数。

然后，程序定义了calculatePolishExpression函数，用于计算波兰表达式的值。在函数中，首先创建一个栈，并对其进行初始化。然后，通过遍历表达式中的每个元素，逐个处理。

如果当前元素是运算符，则从栈中弹出栈顶的两个元素，进行相应的运算，并将结果压入栈中。

如果当前元素是运算数，则将其转换为浮点数，并压入栈中。

最后，返回栈顶的元素，即为表达式的值。

在main函数中，程序首先读取输入的波兰表达式，并调用calculatePolishExpression函数计算表达式的值。最后，将结果使用printf函数输出。

第2题：括号配对

字符串中可能有三种成对的括号，“( )”、“[ ]”、“{ }”。请判断字符串的括号是否都正确配对。无括号也算正确配对。括号交叉算不正确配对，例如"12{34[78}ab]“就不算正确配对。但是一对括号被包含在另一对括号里面，例如"12{ab[8]}“不影响正确性。
时间限制：1000
内存限制：65536
输入
第一行为整数n(n<40)，接下来有n行，每行一个无空格的字符串，长度小于1000。
输出
对每行字符串，如果括号配对，输出"YES”，否则输出"NO”。
样例输入
2
12{ab[8]}
12{34[78}ab]
样例输出
YES
NO

下面是解决这个问题的C语言代码：

#include 
#include 
#include 

#define MAX_SIZE 1000

// 定义栈结构
typedef struct {
    int top;
    char stack[MAX_SIZE];
} Stack;

// 初始化栈
void initialize(Stack *s) {
    s->top = -1;
}

// 判断栈是否为空
int isEmpty(Stack *s) {
    return s->top == -1;
}

// 判断栈是否已满
int isFull(Stack *s) {
    return s->top == MAX_SIZE - 1;
}

// 入栈
void push(Stack *s, char value) {
    if (isFull(s)) {
        printf("Stack is full. Cannot push element.\n");
    } else {
        s->stack[++(s->top)] = value;
    }
}

// 出栈
char pop(Stack *s) {
    if (isEmpty(s)) {
        printf("Stack is empty. Cannot pop element.\n");
        return '\0';
    } else {
        return s->stack[(s->top)--];
    }
}

// 判断括号是否匹配
int isMatchingPair(char opening, char closing) {
    if (opening == '(' && closing == ')') {
        return 1;
    } else if (opening == '[' && closing == ']') {
        return 1;
    } else if (opening == '{' && closing == '}') {
        return 1;
    } else {
        return 0;
    }
}

// 判断字符串中的括号是否配对
int isBalanced(char *expression) {
    Stack stack;
    initialize(&stack);

    int len = strlen(expression);

    for (int i = 0; i < len; i++) {
        if (expression[i] == '(' || expression[i] == '[' || expression[i] == '{') {
            push(&stack, expression[i]);
        } else if (expression[i] == ')' || expression[i] == ']' || expression[i] == '}') {
            if (isEmpty(&stack)) {
                return 0;
            } else if (!isMatchingPair(pop(&stack), expression[i])) {
                return 0;
            }
        }
    }

    return isEmpty(&stack);
}

int main() {
    int n;
    scanf("%d", &n);

    char expression[MAX_SIZE];
    fgets(expression, MAX_SIZE, stdin);

    for (int i = 0; i < n; i++) {
        fgets(expression, MAX_SIZE, stdin);

        // 删除末尾的换行符
        expression[strcspn(expression, "\n")] = '\0';

        if (isBalanced(expression)) {
            printf("YES\n");
        } else {
            printf("NO\n");
        }
    }

    return 0;
}

该程序首先定义了一个栈的结构体，并实现了栈的相关操作函数。

然后，程序定义了isMatchingPair函数，用于判断两个括号是否匹配。

接下来，程序定义了isBalanced函数，用于判断字符串中的括号是否配对。在函数中，首先创建一个栈，并对其进行初始化。然后，遍历字符串中的每个字符：

• 如果当前字符是左括号（‘(’、‘[‘或’{’），则将其入栈。

• 如果当前字符是右括号（‘)’、‘]‘或’}’），则判断栈是否为空。如果栈为空，说明右括号没有对应的左括号，返回0。如果栈不为空，则弹出栈顶的元素，并判断弹出的左括号和当前右括号是否匹配。如果不匹配，返回0。

• 最后，返回栈是否为空。如果栈为空，说明所有括号都正确配对，返回1；否则，返回0。

在main函数中，程序首先读取输入的整数n，表示待判断的字符串数量。然后，使用一个循环依次处理每个字符串。对于每个字符串，调用isBalanced函数判断括号是否配对，并根据结果输出"YES"或"NO"。

第3题：扑克牌排序

假设这里有36张扑克牌，分别为A1_A9,B1B9,C1_C9,D1D9，其中A代表方片，B代表草花，C代表红桃，D代表黑桃，那么，设定如下的排序规则：
1.对于两张卡牌，X1Y1与X2Y2，X1与X2表示A～D，Y1与Y2表示1～9，如果X1与X2不同，那么依照D>C>B>A的方式进行排序
2.假如有X1与X2相同时，那么就比较Y1与Y2的大小。
例如，对于如下的四张牌，有如下的升序排序结果：
D3，C4，A4，C1
升序排序的结果为A4，C1，C4，D3
有人提出了如下的排序策略：
先建立9个队列，用于存放点数的大小，将卡牌依点数存放入各自的队列之中，然后再按队列1到队列9依次出队。
例如，对于上面的结果，依次进队后，结果如下：
队列1：C1；队列3：D3，队列4：C4，A4
将其依次出队后，结果为C1，D3，C4，A4
然后，再建立4个队列，用于存放花色。将卡牌依花色A～D存放入队列1～4中，然后再按队列1到队列4依次出队。
例如，对于上面刚刚出队的序列C1，D3，C4，A4，将其依次进队，结果如下：
队列1：A4；队列3：C1，C4；队列4：D3
将其依次出队后，结果为A4，C1，C4，D3，排序结束。
请根据上面的算法，编写一个用队列对扑克牌排序的程序，要求依照上面的排序规则，根据先花色后点数的方法进行排序。
时间限制：1000
内存限制：65536
输入
输入分为两行，第一行为一个整数n，表示一共有n张牌（1<=n<=100） 第二行用XY的形式表示每一张牌，其中X为A～D，Y为1～9
输出
输出三个部分 第一个部分为第一次进队出队的结果，用Queue1:…表示，共9行，结果用空格分隔，下同 第二部分为第二次进队出队的结果，用QueueA:…表示，共4行 第三部分为一行，即将卡牌排序后的结果（升序排序）
样例输入
8
D8 A6 C3 B8 C5 A1 B5 D3
样例输出
Queue1:A1
Queue2:
Queue3:C3 D3
Queue4:
Queue5:C5 B5
Queue6:A6
Queue7:
Queue8:D8 B8
Queue9:
QueueA:A1 A6
QueueB:B5 B8
QueueC:C3 C5
QueueD:D3 D8
A1 A6 B5 B8 C3 C5 D3 D8
提示
第二次入队出队时，可以复用第一次时9个队列中的4个。所以其实只需要开辟9个队列即可。

下面是一个使用队列进行扑克牌排序的C语言程序：

#include 
#include 
#include 

// 定义队列结构
typedef struct {
    char cards[100][3];  // 存放扑克牌的数组
    int front;  // 队列头指针
    int rear;  // 队列尾指针
} Queue;

// 初始化队列
void initQueue(Queue *queue) {
    queue->front = 0;
    queue->rear = 0;
}

// 判断队列是否为空
int isEmpty(Queue *queue) {
    return queue->front == queue->rear;
}

// 入队
void enqueue(Queue *queue, char *card) {
    strcpy(queue->cards[queue->rear], card);
    queue->rear++;
}

// 出队
void dequeue(Queue *queue, char *card) {
    strcpy(card, queue->cards[queue->front]);
    queue->front++;
}

// 扑克牌排序函数
void sortPoker(int n, char cards[][3]) {
    Queue queues[9];  // 9个队列
    int i, j;
    
    // 初始化队列
    for (i = 0; i < 9; i++) {
        initQueue(&queues[i]);
    }
    
    // 第一次入队出队，按照点数存放到相应的队列中
    for (i = 0; i < n; i++) {
        int index = cards[i][1] - '0';  // 获取点数
        enqueue(&queues[index-1], cards[i]);
    }
    
    // 输出第一次入队出队的结果
    for (i = 0; i < 9; i++) {
        printf("Queue%d:", i+1);
        while (!isEmpty(&queues[i])) {
            char card[3];
            dequeue(&queues[i], card);
            printf(" %s", card);
        }
        printf("\n");
    }
    
    // 第二次入队出队，按照花色存放到相应的队列中
    for (i = 0, j = 0; i < 9; i++) {
        if (i == 0 || i == 5) {
            while (!isEmpty(&queues[i])) {
                char card[3];
                dequeue(&queues[i], card);
                enqueue(&queues[j], card);
            }
            j++;
        }
    }
    
    // 输出第二次入队出队的结果
    for (i = 0; i < 4; i++) {
        printf("Queue%c:", 'A' + i);
        while (!isEmpty(&queues[i])) {
            char card[3];
            dequeue(&queues[i], card);
            printf(" %s", card);
        }
        printf("\n");
    }
    
    // 对队列进行升序排序
    for (i = 0; i < 4; i++) {
        for (j = i + 1; j < 4; j++) {
            if (strcmp(queues[i].cards[queues[i].front], queues[j].cards[queues[j].front]) > 0) {
                Queue temp = queues[i];
                queues[i] = queues[j];
                queues[j] = temp;
            }
        }
    }
    
    // 输出排序后的结果
    for (i = 0; i < 4; i++) {
        while (!isEmpty(&queues[i])) {
            char card[3];
            dequeue(&queues[i], card);
            printf("%s ", card);
        }
    }
    
    printf("\n");
}

int main() {
    int n;
    scanf("%d", &n);
    
    char cards[100][3];
    for (int i = 0; i < n; i++) {
        scanf("%s", cards[i]);
    }
    
    sortPoker(n, cards);
    
    return 0;
}

使用队列进行排序的思路是先根据点数将扑克牌存放到相应的队列中，然后按照队列的顺序进行出队操作，得到第一次进队出队的结果。接着，根据花色将扑克牌再次存放到相应的队列中，再次按照队列的顺序进行出队操作，得到第二次进队出队的结果。最后对4个队列进行升序排序，并输出排序结果。

注意，程序中的队列实现使用了数组，队列的最大长度为100。程序根据输入的扑克牌数量n进行相应的处理，可以处理1到100张扑克牌的排序。

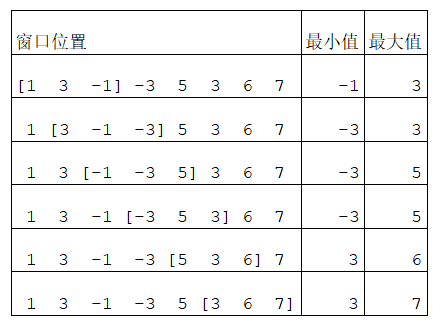
第4题：滑动窗口

给定一个长度为n（n<=10^6）的数组。有一个大小为k的滑动窗口从数组的最左端移动到最右端。你可以看到窗口中的k个数字。窗口每次向右滑动一个数字的距离。
下面是一个例子：
数组是 [1 3 -1 -3 5 3 6 7]， k = 3。

你的任务是得到滑动窗口在每个位置时的最大值和最小值。
时间限制：20000
内存限制：65536
输入
输入包括两行。 第一行包括n和k，分别表示数组的长度和窗口的大小。 第二行包括n个数字。
输出
输出包括两行。 第一行包括窗口从左至右移动的每个位置的最小值。 第二行包括窗口从左至右移动的每个位置的最大值。
样例输入
8 3
1 3 -1 -3 5 3 6 7
样例输出
-1 -3 -3 -3 3 3
3 3 5 5 6 7

这个问题可以使用滑动窗口来解决。我们可以使用双端队列（deque）来辅助实现。

首先，我们需要定义一个双端队列，用于存储当前窗口中的元素。队列中的元素按照从大到小的顺序排列，且队头元素为当前窗口中的最大值。

然后，我们遍历数组，依次将元素添加到双端队列中。在添加元素之前，我们需要进行一些操作：

1. 如果队列不为空且队头元素的下标不在当前窗口的范围内，说明队头元素已经不在当前窗口中，可以将其从队列中删除。

2. 如果队列不为空且队尾元素小于等于当前要添加的元素，说明队尾元素不可能成为后续窗口的最大值，可以将其从队列中删除，以保持队列中元素的有序性。

3. 将当前元素添加到队列的队尾。

在每次添加元素之后，我们可以得到当前窗口的最大值，即队列的队头元素。同时，我们还需要记录当前窗口的最小值。

下面是使用C语言编写的示例代码：

#include 
#include 

// 双端队列结构体
typedef struct {
    int* data;  // 数据数组
    int front;  // 队头指针
    int rear;   // 队尾指针
} Deque;

// 初始化双端队列
void initDeque(Deque* deque, int size) {
    deque->data = (int*)malloc(sizeof(int) * size);
    deque->front = 0;
    deque->rear = -1;
}

// 判断队列是否为空
int isEmpty(Deque* deque) {
    return deque->rear < deque->front;
}

// 在队尾插入元素
void insertRear(Deque* deque, int value) {
    deque->data[++deque->rear] = value;
}

// 删除队头元素
void deleteFront(Deque* deque) {
    deque->front++;
}

// 获取队头元素的值
int getFront(Deque* deque) {
    return deque->data[deque->front];
}

int main() {
    int n, k;
    scanf("%d %d", &n, &k);

    // 读取数组元素
    int* array = (int*)malloc(sizeof(int) * n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &array[i]);
    }

    Deque minDeque, maxDeque;
    initDeque(&minDeque, n);
    initDeque(&maxDeque, n);

    // 处理前k个元素
    for (int i = 0; i < k; i++) {
        // 删除队列中所有小于当前元素的值
        while (!isEmpty(&minDeque) && array[i] <= array[getFront(&minDeque)]) {
            deleteFront(&minDeque);
        }
        while (!isEmpty(&maxDeque) && array[i] >= array[getFront(&maxDeque)]) {
            deleteFront(&maxDeque);
        }

        // 将当前元素添加到队列中
        insertRear(&minDeque, i);
        insertRear(&maxDeque, i);
    }

    // 处理剩余元素
    for (int i = k; i < n; i++) {
        // 输出当前窗口的最小值和最大值
        printf("%d ", array[getFront(&minDeque)]);
        printf("%d ", array[getFront(&maxDeque)]);

        // 删除队列中所有不在当前窗口中的元素
        while (!isEmpty(&minDeque) && getFront(&minDeque) <= i - k) {
            deleteFront(&minDeque);
        }
        while (!isEmpty(&maxDeque) && getFront(&maxDeque) <= i - k) {
            deleteFront(&maxDeque);
        }

        // 删除队列中所有小于当前元素的值
        while (!isEmpty(&minDeque) && array[i] <= array[getFront(&minDeque)]) {
            deleteFront(&minDeque);
        }
        while (!isEmpty(&maxDeque) && array[i] >= array[getFront(&maxDeque)]){
            deleteFront(&maxDeque);
        }

        // 将当前元素添加到队列中
        insertRear(&minDeque, i);
        insertRear(&maxDeque, i);
    }

    // 输出最后一个窗口的最小值和最大值
    printf("%d ", array[getFront(&minDeque)]);
    printf("%d\n", array[getFront(&maxDeque)]);

    // 释放内存
    free(array);
    free(minDeque.data);
    free(maxDeque.data);

    return 0;
}

此代码使用双端队列来维护当前窗口的最小值和最大值。它使用了两个双端队列，一个用于存储当前窗口的最小值，另一个用于存储当前窗口的最大值。代码中的initDeque函数用于初始化双端队列，isEmpty函数用于判断队列是否为空，insertRear函数用于在队尾插入元素，deleteFront函数用于删除队头元素，getFront函数用于获取队头元素的值。

代码通过遍历数组来处理窗口中的元素。在每次添加元素之前，它首先删除队列中不在当前窗口范围内的元素，然后删除队列中所有小于当前元素的值，并将当前元素添加到队列的队尾。在处理第一个窗口时，只需遍历前k个元素。在处理剩余的窗口时，我们需要输出当前窗口的最小值和最大值，并删除队列中不在当前窗口中的元素。

最后，我们输出最后一个窗口的最小值和最大值，并释放动态分配的内存。