《数据挖掘导论》归纳笔记
目录
- 第一章 绪论
- 第二章 数据
-
- 2.0引言
-
- 2.0.1数据类型
- 2.0.2数据的质量
- 2.0.3使数据适合挖掘的预处理步骤
- 2.0.4根据数据联系分析数据
- 2.1数据类型
-
- 2.1.1 属性与度量
- 2.1.2 数据集的类型
- 2.2数据质量
-
- 2.2.1测量和数据收集问题
- 2.2.2 关于应用的问题
- 2.3 数据预处理
-
- 2.3.1聚集
- 2.3.2抽样
- 2.3.3维归约
- 2.3.4特征子集选择
- 2.3.5特征创建
- 2.3.6 离散化和二元化
- 2.3.7变量变换
- 2.4相似性和相异性的度量
-
- 2.4.1基础
- 2.4.2 简单属性之间的相似度和相异度
- 2.4.3数据对象之间的相异度
- 2.4.4数据对象之间的相似度
- 2.4.5邻近性度量的例子
-
- 1.二元数据的相似性度量
- 2.余弦相似度
- 3.广义Jaccard系数
- 4、相关性
- 2.4.6邻近度计算问题
-
- 1.距离度量的标准化和相关性
- 2.组合异种属性的相似度
- 3.使用权值
- 2.4.7选取正确的邻近性度量
- 第三章 探索数据
-
- 3.1 鸢尾花数据集
- 3.2 汇总统计
-
- 3.2.1频率和众数
- 3.2.2 百分位数
- 3.2.3 位置度量:均值和中位数
- 3.2.4散布度量:极差和方差
- 3.2.5 多元汇总统计
- 3.2.6 汇总数据的其他方法
- 3.3 可视化
-
- 3.3.1可视化的动机
- 3.3.2 一般概念
- 3.3.3技术
- 3.3.4 可视化高维数据
- 3.3.5注意事项
- 3.4 OLAP和多维数据分析
-
- 3.4.1用多维数组表示鸢尾花数据
- 3.4.2多维数据:一般情况
- 3.4.3分析多维数据
-
- 1.数据立方体:计算聚集量
- 2.维归约和转轴
- 3.切片和切块
- 4.上卷和下钻
- 第四章 分类:基本概念、决策树与模型评估
-
- 4.1预备知识
- 4.2 解决分类问题的一般方法
- 4.3决策树归纳
-
- 4.3.1决策树的工作原理
- 4.3.2如何建立决策树
-
- 1.Hunt算法
- 2.决策树归纳的设计问题
- 4.3.3表示属性测试条件的方法
- 4.3.4选择最佳划分的度量
-
- 1.二元属性的划分
- 2.标称属性的划分
- 3.连续属性的划分
- 4.增益率
- 4.3.6例子: Web机器人检测
- 4.3.7决策树归纳的特点
- 4.4模型的过分拟合
-
- 4.4.1噪声导致的过分拟合
- 4.4.2缺乏代表性样本导致的过分拟合
- 4.4.3过分拟合与多重比较过程
- 4.4.4泛化误差估计
-
- 1.使用再代入估计
- 2.结合模型复杂度
- 3.估计统计上界
- 4.使用确认集
- 4.4.5处理决策树归纳中的过分拟合
- 4.5评估分类器的性能
-
- 4.5.1保持方法
- 4.5.2随机二次抽样
- 4.5.3交叉验证
- 4.5.4自助法
- 4.6比较分类器的方法
-
- 4.6.1估计准确度的置信区间
- 4.6.2比较两个模型的性能
- 4.6.3比较两种分类法的性能
- 第五章 分类:其他技术
-
- 5.1基于规则的分类器
-
- 5.1.1基于规则的分类器的工作原理
- 5.1.2规则的排序方案
- 5.1.3如何建立基于规则的分类器
- 5.1.4规则提取的直接方法
-
- 1.Learn-One-Rule函数
- 2.顺序覆盖基本原理
- 3.RiPPER算法
- 5.1.5规则提取的间接方法
- 5.1.6基于规则的分类器的特征
- 5.2最近邻分类器
-
- 5.2.1算法
- 5.2.2最近邻分类器的特征
- 5.3贝叶斯分类器
-
- 5.3.1贝叶斯定理
- 5.3.2贝叶斯定理在分类中的应用
- 5.3.3 .朴素贝叶斯分类器
-
- 5.朴素贝叶斯分类器举例
- 6.条件概率的m估计
- 7.朴素贝叶斯分类器的特征
- 5.3.4贝叶斯误差率
- 5.3.5贝叶斯信念网络
- 5.4人工神经网络
-
- 5.4.1感知器
-
- 学习感知器模型
- 5.4.2多层人工神经网络
-
- 1.学习ANN模型
- 2.ANN学习中的设计问题
- 5.4.3人工神经网络的特点
- 5.5支持向量机
-
- 5.5.1最大边缘超平面
- 5.5.2线性支持向量机:可分情况
-
- 1.线性决策边界
- 2.线性分类器的边缘
- 3.学习线性SVM模型
- 5.5.3线性支持向量机:不可分情况
- 5.5.4非线性支持向量机
-
- 1.属性变换
- 2.学习非线性SVM模型
- 3.核技术
- 4.Mercer定理
- 5.5.5支持向量机的特征
- 5.6组合方法
-
- 5.6.1组合方法的基本原理
- 5.6.2构建组合分类器的方法
- 5.6.3偏倚-方差分解
- 5.6.4装袋
- 5.6.5提升
-
- AdaBoost
- 5.6.6随机森林
- 5.6.7组合方法的实验比较
- 5.7不平衡类问题
-
- 5.7.1可选度量
- 5.7.2接受者操作特征曲线
-
- 产生ROC曲线
- 5.7.3代价敏感学习
- 5.7.4基于抽样的方法
- 5.8多类问题
-
-
- 纠错输出编码
-
- 第六章 关联分析:基本概念和算法
-
- 6.1问题定义
- 6.2频繁项集的产生
-
- 6.2.1先验原理
- 6.2.2Apriori算法的频繁项集产生
-
- 算法6.1Apriori算法的频繁项集产生
- 6.2.3候选的产生与剪枝
- 6.2.5计算复杂度
- 6.3规则产生
-
- 6.3.1基于置信度的剪枝
- 6.3.2Apriori算法中规则的产生
- 6.4频繁项集的紧凑表示
-
- 6.4.1极大频繁项集
- 6.4.2闭频繁项集
- 6.5产生频繁项集的其他方法
- 6.6FP增长算法
-
- 6.6.1 FP树表示法
- 6.6.2FP增长算法的频繁项集产生
- 6.7关联模式的评估
-
-
- 1.其他客观兴趣度度量
- 2.客观度量的一致性
- 3.客观度量的性质
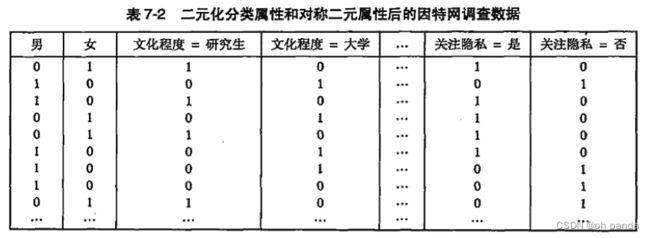
- 6.7.2多个二元变量的度量
- 6.7.3辛普森悖论
-
- 6.8倾斜支持度分布的影响
- 第七章 关联分析:高级概念
-
- 7.1处理分类属性
- 7.2处理连续属性
-
- 7.2.1基于离散化的方法
- 7.2.2基于统计学的方法
- 7.2.3非离散化方法
- 7.3处理概念分层
- 7.4序列模式
-
- 7.4.2序列模式发现
- 算法7.1序列模式发现的类Apriori算法
- 7.4.3时限约束
- 7.5子图模式
-
- 7.5.1图与子图
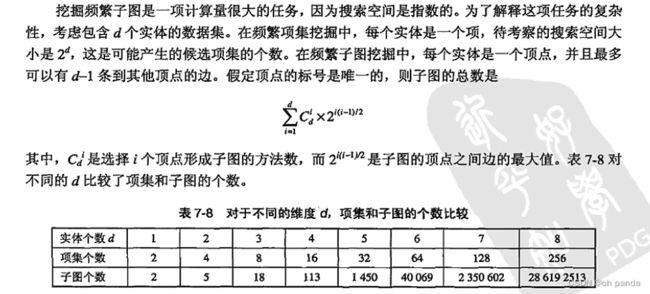
- 7.5.2频繁子图挖掘
- 7.5.3类Apriori方法
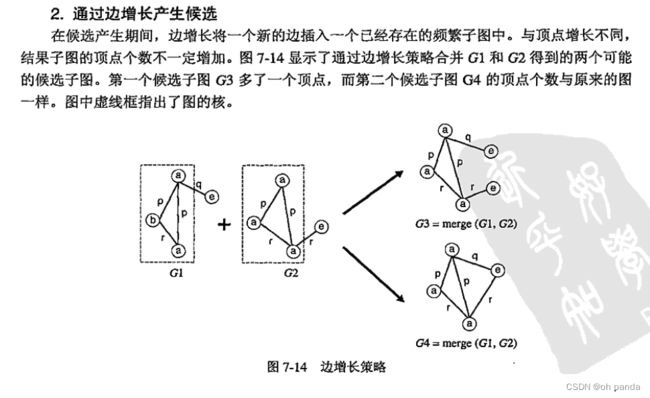
- 7.5.4候选产生
- 7.5.5候选剪枝
- 7.6非频繁模式
-
- 7.6.1负模式
- 7.6.2负相关模式
- 7.6.3非频繁模式、负模式和负相关模式比较
- 7.6.4挖掘有趣的非频繁模式的技术
- 7.6.5基于挖掘负模式的技术
- 7.6.6基于支持度期望的技术
- 算法7.2挖掘间接关联的算法
- 第八章 聚类分析:基本概念和算法
-
- 8.1概述
-
- 8.1.1什么是聚类分析
- 8.1.2不同的聚类类型
- 8.1.3 不同的簇类型
- 8.2K均值
-
- 8.2.1基本K均值算法
- 算法8.1基本K均值算法
- 8.2.2 K均值:附加的问题
- 8.2.3二分K均值
- 算法8.2二分K均值算法
- 8.2.4 K均值和不同的簇类型
- 8.2.5优点与缺点
- 8.2.6 K均值作为优化问题
- 8.3凝聚层次聚类
-
- 8.3.1基本凝聚层次聚类算法
- 8.3.2特殊技术
- 8.3.3簇邻近度的Lance-Williams 公式
- 8.3.5优点与缺点
- 8.4 DBSCAN
-
- 8.4.1传统的密度:基于中心的方法
- 8.4.2DBSCAN算法
- 8.4.3优点与缺点
- 8.5簇评估
-
- 8.5.1概述
- 8.5.2非监督簇评估:使用凝聚度和分离度
- 8.5.3非监督簇评估:使用邻近度矩阵
- 8.5.4层次聚类的非监督评估
- 8.5.5确定正确的簇个数
- 8.5.6聚类趋势
- 8.5.7簇有效性的监督度量
- 8.5.8评估簇有效性度量的显著性
- 第九章 聚类分析:其他问题与算法
-
- 9.1数据、簇和聚类算法的特性
-
- 9.1.1例子:比较K均值和DBSCAN
- 9.1.2数据特性
- 9.1.3簇特性
- 9.1.4聚类算法的一般特性
- 9.2基于原型的聚类
-
- 9.2.1模糊聚类
- 算法9.1基本模糊c均值算法
- 9.2.2使用混合模型的聚类
- 算法9.2EM算法
-
- 4.使用EM算法的混合模型聚类的优点和局限性
- 9.2.3自组织映射
-
- 1.SOM算法
- 算法9.3基本SOM算法
-
- 2.应用
- 9.3基于密度的聚类
-
- 9.3.1基于网格的聚类
- 算法9.4基本的基于网格的聚类算法
-
- 3.由稠密网格单元形成簇
- 4、优点与局限性
- 9.3.2子空间聚类
-
- 1.CLIQUE
- 算法9.5CLIQUE算法
-
-
- 2.CLIQUE的优点与局限性
- 9.3.3 DENCLUE:基于密度聚类的一种基于核的方案
- 算法9.6 DENCLUE 算法
-
- 1、核密度估计
- 2.实现问题
- 3.DENCLUE的优点与局限性
-
- 9.4基于图的聚类
-
- 9.4.1稀疏化
- 9.4.2最小生成树聚类
- 算法9.7MST分裂层次聚类算法
- 9.4.3OPOSSUM:使用METIS的稀疏相似度最优划分
- 算法9.8 OPoSSUM 聚类算法
- 9.4.4Chameleon:使用动态建模的层次聚类
-
- 2.Chameleon算法
- 算法9.9Chameleon算法
-
- 4.优点与局限性
- 9.4.5共享最近邻相似度
- 算法9.10计算共享最近邻相似度
- 9.4.6Jarvis-Patrick聚类算法
- 算法9.11Jarvis-Patrick聚类算法
- 9.4.7 SNN密度
- 9.4.8基于SNN密度的聚类
- 算法9.12基于SNN密度的聚类算法
- 9.5可伸缩的聚类算法
-
- 9.5.1 可伸缩:一般问题和方法
- 9.5.2BIRCH
- 算法9.13BIRCH
- 9.5.3 CURE
- 算法9.14 CURE
- 9.6使用哪种聚类算法
- 10.1预备知识
-
- 10.1.1异常的成因
- 10.1.2异常检测方法
- 10.1.3类标号的使用
- 10.1.4问题
- 10.2统计方法
-
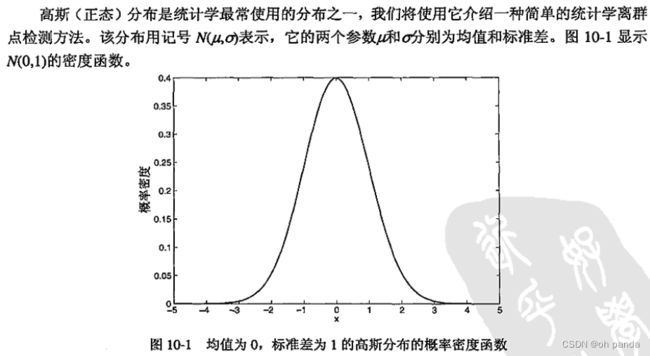
- 10.2.1检测一元正态分布中的离群点
- 10.2.2多元正态分布的离群点
- 10.2.3异常检测的混合模型方法
- 算法10.1基于似然的离群点检测
- 10.3基于邻近度的离群点检测
- 10.4基于密度的离群点检测
-
- 10.4.1使用相对密度的离群点检测
- 10.4.2优点与缺点
- 10.5基于聚类的技术
-
- 10.5.1评估对象属于簇的程度
- 10.5.2离群点对初始聚类的影响
- 10.5.3使用簇的个数
第一章 绪论
一、数据挖掘定义:在大型数据存储库中,自动地发现有用信息的过程。
二、数据挖掘要解决的问题
1. 可伸缩:要处理海量数据集(如数拍字节),算法必须可伸缩
2.高维性:现在许多数据集有成百上千的属性
3.异种数据和复杂数据:许多数据集包含不同类型的属性,如包含超链接的web页面集
4.数据的所有权与分布:数据在地理上属于多个机构,需要分布式数据挖掘技术
5.非传统的分析:分析的数据集不是精心设计的实验结果,通常代表数据的时机性样本,而不是随机样本
三、数据挖掘任务
1.预测任务
根据其他属性的值,预测特定属性的值,如预测建模
2.描述任务
概括数据中的潜在联系的模式,如关联分析,聚类分析,异常检测等
第二章 数据
2.0引言
2.0.1数据类型
1.定性的,定量的
2.数据集可以看作数据对象的集合
3.数据对象有时也叫做记录、点、向量、模式、事件、案例、样本、观测或实体。
4.属性有时也叫做变量、特性、字段、特征或维。
2.0.2数据的质量
数据并非完美,数据挖掘技术可以忍受某种程度上的不完美,但提高数据质量可以改进分析结果的质量,如解决离群点,数据遗漏,重复等问题
2.0.3使数据适合挖掘的预处理步骤
原始数据处理后更适合分析,处理一方面提高数据的质量,一方面让数据更适应特定的数据挖掘技术或工具
2.0.4根据数据联系分析数据
找出数据对象之间的联系,利用联系来进行分析,如计算对象之间的相似度或距离,然后根据相似度或距离进行分析—聚类、分类、异常检测
2.1数据类型
2.1.1 属性与度量
1. 什么是属性?
属性(attribute)定义:对象的特质或特性,因对象而异
测量标度(measurement scale)定义:把对象的属性与数值或符号值相关联的规则
2. 属性类型
属性的性质不必与用来度量它的值的性质相同,换句话说属性的值可能具有不同于属性本身的性质
如谈论雇员的平均年龄是有意义的,但是谈论雇员的平均ID却毫无意义。
3. 属性的不同类型
数值的如下性质(操作)常常用来描述属性
定义四种属性类型:标称(nominal)、序数(ordinal)、区间(interval)和比率
每种属性类型拥有其上方属性类型上的所有性质和操作。
对于标称、序数和区间属性合法的任何性质或操作,对于比率属性也合法。
对于某种属性类型合适的操作,对其上方的属性类型就不一定合适。
允许的变换
例如长度分别用米和英尺度量,其属性意义并没有改变
当使用保持属性意义的变换对属性进行变换时,它们产生的结果相同。
4. 用值的个数描述属性
离散的( discrete)
离散属性具有有限个值或无限可数个值。是可分类的,如邮政编码或D号,也可以是数值的,如计数。通常,离散属性用整数变量表示。
二元属性(binary attribute)是离散属性的一种特殊情况,并只接受两个值,如真/假、男/女
计数属性(count attribute)是离散的,也是比率属性。
连续的(continuous)
连续属性是取实数值的属性。如温度、高度或重量等属性。通常,连续属性用浮点变量表示。
5.非对称的属性
对于非对称的属性(asymmetric attribute),出现非零属性值才是重要的。
只有非零值才重要的二元属性是非对称的二元属性,这类属性对于关联分析特别重要。
2.1.2 数据集的类型
为方便起见,我们将数据集类型分成三组:记录数据、基于图形的数据和有序的数据。
1.数据集的一般特性
(1)维度(dimensionality)数据集的维度是数据集中的对象具有的属性数目。分析高维数据有时会陷入所谓维灾难( curse ofdimensionality)。数据预处理的一个重要动机就是减少维度,称为维归约(dimensionality reduction)。
(2)稀疏性(sparsity)有些数据集,如具有非对称特征的数据集,一个对象的大部分属性上的值都为0;在许多情况下,非零项还不到1%。有些数据挖掘算法仅适合处理稀疏数据。
(3)分辨率(resolution)常常可以在不同的分辨率下得到数据,并且在不同的分辨率下数据的性质也不同。例如,在几米的分辨率下,地球表面看上去很不平坦,但在数十公里的分辨率下却相对平坦。数据的模式也依赖于分辨率。如果分辨率太高,模式可能看不出,或者掩埋在噪声中;如果分辨率太低,模式可能不出现。例如,几小时记录一下气压变化可以反映出风暴等天气系统的移动;而在月的标度下,这些现象就检测不到。
2.记录数据
许多数据挖掘任务都假定数据集是记录(数据对象〉的汇集。每个记录包含固定的数据字段(属性)集。
见下图。对于记录数据的大部分基本形式,记录之间或数据字段之间没有明显的联系,并且每个记录(对象)具有相同的属性集。记录数据通常存放在平展文件或关系数据库中。

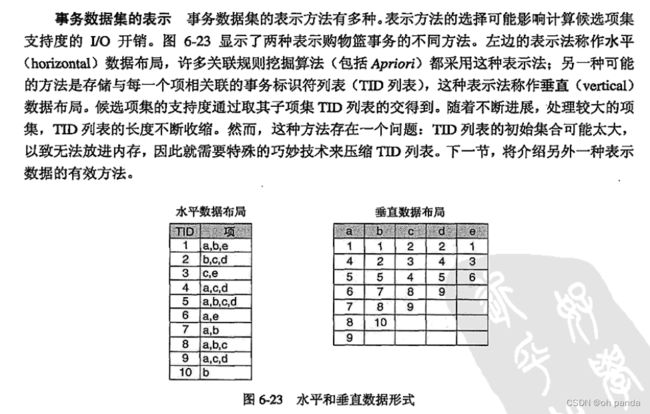
事务数据或购物篮数据
事务数据(transaction data)是一种特殊类型的记录数据,其中每个记录(事务)涉及一系列的项。
考虑一个杂货店。顾客一次购物所购买的商品的集合就构成一个事务,而购买的商品是项。这种类型的数据称作购物篮数据(market basket data),因为记录中的项是顾客“购物篮”中的商品。
事务数据是项的集合的集族,但是也能将它视为记录的集合,其中记录的字段是非对称的属性。
这些属性常常是二元的,指出商品是否已买。更一般地,这些属性还可以是离散的或连续的,例如表示购买的商品数量或购买商品的花费。
数据矩阵
如果一个数据集族中的所有数据对象都具有相同的数值属性集,则数据对象可以看作多维空间中的点(向量),其中每个维代表对象的一个不同属性。
这样的数据对象集可以用一个m x n的矩阵表示,其中m行,一个对象一行;n列,一个属性一列。(也可以将数据对象用列表示,属性用行表示。)这种矩阵称作数据矩阵(data matrix)或模式矩阵(pattern matrix)。
数据矩阵是记录数据的变体,但是,由于它由数值属性组成,可以使用标准的矩阵操作对数据进行变换和处理,因此,对于大部分统计数据,数据矩阵是一种标准的数据格式。
稀疏数据矩阵
稀疏数据矩阵是数据矩阵的一种特殊情况,其中属性的类型相同并且是非对称的,即只有非零值才是重要的。
事务数据是仅含0-1元素的稀疏数据矩阵的例子。另一个常见的例子是文档数据。
特别地,如果忽略文档中词(术语)的次序,则文档可以用词向量表示,其中每个词是向量的一个分量(属性),而每个分量的值是对应词在文档中出现的次数。文档集合的这种表示通常称作文档-词矩阵(document-term matrix)。上图显示了一个文档-词矩阵。文档是该矩阵的行,而词是矩阵的列。
实践应用时,仅存放稀疏数据矩阵的非零项。
3.基于图形的数据
考虑两种特殊情况:
(1)图形捕获数据对象之间的联系
(2)数据对象本身用图形表示。
带有对象之间联系的数据
对象之间的联系常常携带重要信息。在这种情况下,数据常常用图形表示。一般把数据对象映射到图的结点,而对象之间的联系用对象之间的链和诸如方向、权值等链性质表示。
考虑万维网上的网页,页面上包含文本和指向其他页面的链接。为了处理搜索查询,Web搜索引擎收集并处理网页,提取它们的内容。众所周知,指向或出自每个页面的链接包含了大量该页面与查询相关程度的信息,因而必须考虑。如下图所示
具有图形对象的数据
如果对象具有结构,即对象包含具有联系的子对象,则这样的对象常常用图形表示。
例如,化合物的结构可以用图形表示,其中结点是原子,结点之间的链是化学键。下图给出化合物苯的分子结构示意图,图形表示可以确定何种子结构频繁地出现在化合物的集合中,并且查明这些子结构中是否有某种子结构与诸如熔点或生成热等特定的化学性质有关。
子结构挖掘是数据挖掘中分析这类数据的一个分支,将在7.5节讨论。

4.有序数据
对于某些数据类型,属性具有涉及时间或空间序的联系。
下面介绍各种类型的有序数据,并显示在图2-4中。

时序数据
时序数据(sequential data)也称时间数据( temporal data),可以看作记录数据的扩充,其中每个记录包含一个与之相关联的时间。
考虑存储事务发生时间的零售事务数据。时间信息可以帮助我们发现“万圣节前夕糖果销售达到高峰”之类的模式。时间也可以与每个属性相关联,例如,每个记录可以是一位顾客的购物历史,包含不同时间购买的商品列表。使用这些信息,就有可能发现“购买DVD播放机的人趋向于在其后不久购买DVD”之类的模式。
序列数据
序列数据(sequence data)是一个数据集合,它是各个实体的序列,如词或字母的序列。
除没有时间戳之外,它与时序数据非常相似,只是有序序列考虑项的位置。例如,动植物的遗传信息可以用称作基因的核苷酸的序列表示。与遗传序列数据有关的许多问题都涉及由核苷酸序列的相似性预测基因结构和功能的相似性。图2-4b 显示用4种核苷酸表示的一段人类基因码。
时间序列数据
时间序列数据(time series data)是一种特殊的时序数据,其中每个记录都是一个时间序列(time series),即一段时间以来的测量序列。
例如,金融数据集可能包含各种股票每日价格的时间序列对象。再例如,考虑图2-4c,该图显示明尼阿波利斯从1982年到1994年的月平均气温的时间序列。
在分析时间数据时,重要的是要考虑时间自相关( temporal autocorrelation),即如果两个测量的时间很接近,则这些测量的值通常非常相似。
空间数据
有些对象除了其他类型的属性之外,还具有空间属性,如位置或区域。
空间数据的一个例子是从不同的地理位置收集的气象数据(降水量、气温、气压)。空间数据的一个重要特点是空间自相关性(spatial autocorrelation),即物理上靠近的对象趋向于在其他方面也相似。这样,地球上相互靠近的两个点通常具有相近的气温和降水量。
5.处理非记录数据
大部分数据挖掘算法都是为记录数据或其变体(如事务数据和数据矩阵)设计的。通过从数据对象中提取特征,并使用这些特征创建对应于每个对象的记录,针对记录数据的技术也可以用于非记录数据。
考虑前面介绍的化学结构数据。给定一个常见的子结构集合,每个化合物都可以用一个具有二元属性的记录表示,这些二元属性指出化合物是否包含特定的子结构。这样的表示实际上是事务数据集,其中事务是化合物,而项是子结构。
在某些情况下,容易用记录形式表示数据,但是这类表示并不能捕获数据中的所有信息。
考虑这样的时间空间数据,它由空间网格每一点上的时间序列组成。通常,这种数据存放在数据矩阵中,其中每行代表一个位置,而每列代表一个特定的时间点。然而,这种表示并不能明确地表示属性之间存在的时间联系以及对象之间存在的空间联系。
但并不是说这种表示不合适,而是说分析时必须考虑这些联系。例如,在使用数据挖掘技术时,假定属性之间在统计上是相互独立的并不是一个好主意。
2.2数据质量
数据挖掘着眼于两个方面:(1)数据质量问题的检测和纠正,(2〉使用可以容忍低质量数据的算法。第一步的检测和纠正,通常称作数据清理(data cleaning)。
2.2.1测量和数据收集问题
以下关注数据测量和收集方面的数据质量问题。我们先定义测量误差和数据收集错误,然后考虑涉及测量误差的各种问题:噪声、伪像、偏倚、精度和准确率。最后讨论可能同时涉及测量和数据收集的数据质量问题:离群点、遗漏和不一致的值、重复数据。
1.测量误差和数据收集错误
术语测量误差(measurement error)是指测量过程中导致的问题。
一个常见的问题是:在某种程度上,记录的值与实际值不同。
对于连续属性,测量值与实际值的差称为误差(error)。
术语数据收集错误(data collection error)是指诸如遗漏数据对象或属性值,或不当地包含了其他数据对象等错误。例如,一种特定种类动物研究可能包含了相关种类的其他动物,它们只是表面上与要研究的种类相似。
2.噪声和伪像
噪声是测量误差的随机部分。这可能涉及值被扭曲或加入了谬误对象。
图2-5显示被随机噪声干扰前后的时间序列。如果在时间序列上添加更多的噪声,形状将会消失。图2-6显示了三组添加一些噪声点(用“+”表示)前后的数据点集。注意,有些噪声点与非噪声点混在一起。

术语“噪声”通常用于包含时间或空间分量的数据。
在这些情况下,常常可以使用信号或图像处理技术降低噪声,完全消除噪声通常是困难的,而许多数据挖掘工作都关注设计鲁棒算法(robust algorithm),即在噪声干扰下也能产生可以接受的结果。
数据错误可能是更确定性现象的结果,如一组照片在同一地方出现条纹。
数据的这种确定性失真常称作伪像(〈artifact>。
3.精度、偏倚和准确率
在统计学和实验科学中,测量过程和结果数据的质量用精度和偏倚度量。
定义2.3 精度(precision)(同一个量的)重复测量值之间的接近程度。
定义2.4 偏倚(bias)测量值与被测量之间的系统的变差。
精度通常用值集合的标准差度量,而偏倚用值集合的均值与测出的已知值之间的差度量。
只有那些通过外部手段能够得到测量值的对象,偏倚才是可确定的。
假定我们有1克质量的标准实验室重量,并且想评估实验室的新天平的精度和偏倚。我们称重5次,得到下列值:{1.015,0.9901.013,1.001,0.986}。这些值的均值是1.001,因此偏倚是0.001。用标准差度量,精度是0.013
通常使用更一般的术语准确率表示数据测量误差的程度。
定义2.5 准确率〈 accuracy)被测量的测量值与实际值之间的接近度。
4.离群点
离群点(outlier〉是在某种意义上具有不同于数据集中其他大部分数据对象的特征的数据对象,或是相对于该属性的典型值来说不寻常的属性值。我们也称其为异常(anomalous)对象或异常值。
区别噪声和离群点这两个概念是非常重要的。离群点可以是合法的数据对象或值。
5.遗漏值
一个对象遗漏一个或多个属性值的情况并不少见。有时可能会出现信息收集不全的情况
有许多处理遗漏值的策略,每种策略可能适用于特定的情况。这些策略在下面列出,同时我们指出它们的优缺点。
-删除数据对象或属性 一种简单而有效的策略是删除具有遗漏值的数据对象。
-估计遗漏值 有时,遗漏值可以可靠地估计。例如,在考虑以大致平滑的方式变化的、具有少量但分散的遗漏值的时间序列时,遗漏值可以使用其他值来估计(插值)。
-在分析时忽略遗漏值
6.不一致的值
数据可能包含不一致的值。比如地址字段列出了邮政编码和城市名,但是有的邮政编码区域并不包含在对应的城市中。可能是人工输入该信息时录颠倒了两个数字,或许是在手写体扫描时错读了一个数字。
7、重复数据
为了检测并删除这种重复,必须处理两个主要问题。
首先,如果两个对象实际代表同一个对象,则对应的属性值必然不同,必须解决这些不一致的值;
其次,需要避免意外地将两个相似但并非重复的数据对象(如两个人具有相同姓名〉合并在一起。
术语去重复(deduplication)通常用来表示处理这些问题的过程。
2.2.2 关于应用的问题
时效性
有些数据收集后就开始老化。比如说,如果数据提供正在发生的现象或过程的快照,如顾客的购买行为或Web浏览模式。则快照只代表有限时间内的真实情况。如果数据已经过时,则基于它的模型和模式也已经过时。
相关性
可用的数据必须包含应用所需要的信息。考虑构造一个模型,预测交通事故发生率。如果忽略了驽驶员的年龄和性别信息,那么除非这些信息可以间接地通过其他属性得到,否则模型的精度可能是有限的。
确保数据集中的对象相关不太容易。一个常见问题是抽样偏倚(sampling bias),指样本包含的不同类型的对象与它们在总体中的出现情况不成比例。
例如调查数据只反映对调查做出响应的那些人的意见。
由于数据分析的结果只反映现有的数据,抽样偏倚通常导致不正确的分析。
关于数据的知识
理想情况下,数据集附有描述数据的文档。
文档的质量好坏决定它是支持还是干扰其后的分析。
例如,如果文档标明若干属性是强相关的,则说明这些属性可能提供了高度冗余的信息,我们可以决定只保留一个。(考虑销售税和销售价格。)
其他应该说明的重要特性是数据精度、特征的类型(标称的、序数的、区间的、比率的)、测量的刻度(如长度用米还是英尺)和数据的来源。
2.3 数据预处理
讨论应当采用哪些预处理步骤,让数据更加适合挖掘。
聚集。
抽样。
维归约。
特征子集选择。
特征创建。
离散化和二元化。
变量变换。
粗略地说,这些项目分为两类,即选择分析所需要的数据对象和属性以及创建/改变属性。
术语注记:下面,我们有时将根据习惯用法,使用特征(feature)或变量(variable)指代属性(attribute)。
2.3.1聚集
聚集(aggregation)将两个或多个对象合并成单个对象
问题是如何创建聚集事务,何合并所有记录的每个属性的值。
定量属性(如价格)通常通过求和或求平均值进行聚集。
定性属性〈如商品)可以忽略或汇总成在一个商店销售的所有商品的集合。
2.3.2抽样
抽样是一种选择数据对象子集进行分析的常用方法。
有效抽样的主要原理如下:
如果样本是有代表性的,则使用样本与使用整个数据集的效果几乎一样。
而样本是有代表性的,前提是它近似地具有与原数据集相同的(感兴趣的)性质。如果数据对象的均值(乎均值〉是感兴趣的性质,而样本具有近似于原数据集的均值,则样本就是有代表性的。
1.抽样方法
最简单的抽样是简单随机抽样(simple random sampling)。
对于这种抽样,选取任何特定项的概率相等。
随机抽样有两种变形(其他抽样技术也一样):
(1)无放回抽样——每个选中项立即从构成总体的所有对象某中删除;
(2)有放回抽样——对象被选中时不从总体中删除。
分层抽样(stratified sampling)
它从预先指定的组开始抽样。在最简单的情况下,尽管每组的大小不同,但是从每组抽取的对象个数相同。另一种变形是从每一组抽取的对象数量正比于该组的大小。
抽样与信息损失
一旦选定抽样技术,就需要选择样本容量。较大的样本容量增大了样本具有代表性的概率,但也抵消了抽样带来的许多好处。反过来,使用较小容量的样本,可丢失模式,或检测出错误的模式。
图2-9a显示包含8 000个二维点的数据集,而图2-9b和图2-9c显示从该数据集抽取的容量分别为2000和500的样本。该数据集的大部分结构都出现在2 000个点的样本中,但是许多结构在500个点的样本中丢失了。

确定适当的样本容量
给定一个数据集,它包含少量容量大致相等的组。从每组至少找出一个代表点。假定每个组内的对象高度相似,但是不同组中的对象不太相似。还假定组的个数不多(例如,10个组)。图2-10a显示了一个理想簇(组)的集合,这些点可能从中抽取。
使用抽样可以有效地解决该问题。-种方法是取数据点的一个小样本,逐对计算点之间的相似性,然后形成高度相似的点组。从这些组每组取一个点,则可以得到具有代表性的点的集合。然而,按照该方法,我们需要确定样本的容量,它以很高的概率确保得到期望的结果,即从每个簇至少找出一个代表点

2.渐进抽样
合适的样本容量可能很难确定,因此有时需要使用自适应(adaptive)或渐进抽样(progre-ssive sampling)方法。
这些方法从一个小样本开始,然后增加样本容量直至得到足够容量的样本。
2.3.3维归约
数据集可能包含大量特征。考虑一个文档的集合,其中每个文档是一个向量,其分量是文档中出现的每个词的频率。在这种情况下,通常有成千上万的属性(分量),每个代表词汇表中的一个词。
维归约有多方面的好处。关键的好处是,如果维度(数据属性的个数)较低,许多数据挖掘算法的效果就会更好。这一部分是因为维归约可以删除不相关的特征并降低噪声,一部分是因为维灾难。
另一个好处是维归约可以使模型更容易理解,因为模型可能只涉及较少的属性。此外,维归约也可以更容易让数据可视化。即使维归约没有将数据归约到二维或三维,数据也可以通过观察属性对或三元组属性达到可视化,并且这种组合的数目也会大大减少。
最后,使用维归约降低了数据挖掘算法的时间和内存需求。
术语“维归约”通常用于这样的技术:通过创建新属性,将一些旧属性合并在一起来降低数据集的维度。
通过选择旧属性的子集得到新属性,这种维归约称为特征子集选择或特征选择。
1.维灾难
维灾难是指这样的现象:随着数据维度的增加,许多数据分析变得非常困难。
2.维归约的线性代数技术
维归约的一些最常用的方法是使用线性代数技术,将数据由高维空闾投影到低维空间,特别是对于连续数据。
主成分分析(Principal Components Analysis,PCA)是一种用于连续属性的线性代数技术,它找出新的属性(主成分),这些属性是原属性的线性组合,是相互正交的(orthogonal),并且捕获了数据的最大变差。
例如,前两个主成分是两个正交属性,是原属性的线性组合,尽可能多地捕获了数据的变差。奇异值分解(Singular Value Decomposition,sVD)是一种线性代数技术,它与PCA有关,并且也用于维归约。
2.3.4特征子集选择
降低维度的另一种方法是仅使用特征的一个子集。
冗余特征重复了包含在一个或多个其他属性中的许多或所有信息。例如,一种产品的购买价格和所支付的销售税额包含许多相同的信息。
不相关特征包含对于手头的数据挖掘任务几乎完全没用的信息,例如学生的D号码对于预测学生的总平均成绩是不相关的。
冗余和不相关的特征可能降低分类的准确率,影响所发现的聚类的质量。
特征选择的理想方法是:将所有可能的特征子集作为感兴趣的数据挖掘算法的输入,然后选取产生最好结果的子集。这种方法的优点是反映了最终使用的数据挖掘算法的目的和偏爱。
然而,由于涉及n个属性的子集多达2^n个,这种方法在大部分情况下行不通,因此需要其他策略。
有三种标准的特征选择方法:嵌入、过滤和包装。
嵌入方法(embedded approach)
特征选择作为数据挖掘算法的一部分是理所当然的。特别是在数据挖掘算法运行期间,算法本身决定使用哪些属性和忽略哪些属性。构造决策树分类器的算法(在第4章讨论〉通常以这种方式运行。
过滤方法(filter approach)
使用某种独立于数据挖掘任务的方法,在数据挖掘算法运行前进行特征选择,例如我们可以选择属性的集合,它的属性对之间的相关度尽可能低。
包装方法(wrapper approach)
这些方法将目标数据挖掘算法作为黑盒,使用类似于前面介绍的理想算法,但通常并不枚举所有可能的子集来找出最佳属性子集。
由于嵌入方法与具体的算法有关,这里我们只进一步讨论过滤和包装方法。
1、特征子集选择体系结构
可以将过滤和包装方法放到一个共同的体系结构中。
特征选择过程可以看作由四部分组成:子集评估度量、控制新的特征子集产生的搜索策略、停止搜索判断和验证过程。
过滤方法和包装方法的唯一不同是它们使用了不同的特征子集评估方法。
对于包装方法,子集评估使用目标数据挖掘算法:
对于过滤方法,子集评估技术不同于目标数据挖掘算法。下面的讨论提供了该方法的一些细节,汇总在图2-11中。

从概念上讲,特征子集选择是搜索所有可能的特征子集的过程。可以使用许多不同类型的搜索策略,但是搜索策略的计算花费应当较低,并且应当找到最优或近似最优的特征子集。通常不可能同时满足这两个要求,因此需要折中权衡。
因为子集的数量可能很大,考察所有的子集可能不现实,因此需要某种停止搜索判断。其策略通常基于如下一个或多个条件:迭代次数,子集评估的度量值是否最优或超过给定的阅值,一个特定大小的子集是否已经得到,大小和评估标准是否同时达到,使用搜索策略得到的选择是否可以实现改进。
2.特征加权
特征加权是另一种保留或删除特征的办法。特征越重要,所赋予的权值越大,而不太重要的特征赋予较小的权值。
2.3.5特征创建
常常可以由原来的属性创建新的属性集,更有效地捕获数据集中的重要信息。
三种创建新属性的相关方法:特征提取、映射数据到新的空间和特征构造。
1.特征提取
由原始数据创建新的特征集称作特征提取(feature extraction)。
考虑照片的集合,按照照片是否包含人脸分类。原始数据是像素的集合,因此对于许多分类算法都不适合。
最常使用的特征提取技术都是高度针对具体领域的。
一旦数据挖掘用于一个相对较新的领域,一个关键任务就是开发新的特征和特征提取方法。
2.映射数据到新的空间
通过对该时间序列实施傅里叶变换(Fourier transform),将它转换成频率信息明显的表示,就能检测到这些模式。
对于时间序列,傅里叶变换产生其属性与频率有关的新数据对象就足够了。
除傅里叶变换外,对于时间序列和其他类型的数据,经证实小波变换(wavelet transform)也是非常有用的。
3.特征构造
有时,原始数据集的特征具有必要的信息,但其形式不适合数据挖掘算法。在这种情况下,一个或多个由原特征构造的新特征可能比原特征更有用。
2.3.6 离散化和二元化
有些数据挖掘算法,特别是某些分类算法,要求数据是分类属性形式。发现关联模式的算法要求数据是二元属性形式。这样,常常需要将连续属性变换成分类属性(离散化,discretization),并且连续和离散属性可能都需要变换成一个或多个二元属性(二元化,binarization)。
离散化和二元化一般要满足这样一种判别标准,它与所考虑的数据挖掘任务的性能好坏直接相关。
1.二元化
一种分类属性二元化的简单技术如下:如果有m 个分类值,则将每个原始值唯一地赋予区间[0, m-1]中的一个整数。
如果属性是有序的,则赋值必须保持序关系。(注意,即使属性原来就用整数表示,但如果这些整数不在区间[0, m-1]中,则该过程也是必需的。)
然后,将这m个整数的每一个都变换成一个二进制数。由于需要n =log2 m 个二进位表示这些整数,因此要使用n个二元属性表示这些二进制数。例如,一个具有5个值{awful, poor, OK, good, great}的分类变量需要三个二元变量。
2.连续属性离散化
通常,离散化应用于在分类或关联分析中使用到的属性上。一般来说,离散化的效果取决于所使用的算法,以及用到的其他属性。然而,属性离散化通常单独考虑。
连续属性变换成分类属性涉及两个子任务:决定需要多少个分类值,以及确定如何将连续属性值映射到这些分类值。在第一步中,将连续属性值排序后,通过指定n-1个分割点(split point)把它们分成n个区间。
在颇为平凡的第二步中,将一个区间中的所有值映射到相同的分类值。因此,离散化问题就是决定选择多少个分割点和确定分割点位置的问题。
-非监督离散化
用于分类的离散化方法之间的根本区别在于使用类信息(监督,supervised)还是不使用类信息(非监督,unsupervised)。如果不使用类信息,则常使用一些相对简单的方法。
例如,等宽〈equal width)方法将属性的值域划分成具有相同宽度的区间,而区间的个数由用户指定。这种方法可能受离群点的影响而性能不佳,因此等频率(equal frequncy)或等深(equal depth)方法通常更为可取。
等频率方法试图将相同数量的对象放进每个区间。作为非监督离散化的另一个例子,可以使用诸如均值(见第8章)等聚类方法。最后,目测检查数据有时也可能是一种有效的方法。
-监督离散化
上面介绍的离散化方法通常比不离散化好,但是记住最终目的并使用附加的信息(类标号)常常能够产生更好的结果。这并不奇怪,因为未使用类标号知识所构造的区间常常包含混合的类标号。
一种概念上的简单方法是以极大化区间纯度的方式确定分割点。然而,实践中这种方法可能需要人为确定区间的纯度和最小的区间大小。
为了解决这一问题,一些基于统计学的方法用每个属性值来分隔区间,并通过合并类似于根据统计检验得出的相邻区间来创建较大的区间。基于熵的方法是最有前途的离散化方法之一,我们将给出一种简单的基于熵的方法。
直观上,区间的熵是区间纯度的度量。如果一个区间只包含一个类的值(该区间非常纯),则其值为0并且不影响总熵。
如果一个区间中的值类出现的频率相等(该区间尽可能不纯),则其熵最大。
一种划分连续属性的简单方法是;开始,将初始值切分成两部分,让两个结果区间产生最小嫡。该技术只需要把每个值看作可能的分割点即可,因为假定区间包含有序值的集合。然后,取一个区间,通常选取具有最大滴的区间,重复此分割过程,直到区间的个数达到用户指定的个数,或者满足终止条件。
3.具有过多值的分类属性
分类属性有时可能具有过多的值。如果分类属性是序数属性,则可以使用类似于处理连续属性的技术,以减少分类值的个数。
然而,如果分类属性是标称的,就需要使用其他方法。考虑一所大学,它有许多系,因而系名属性可能具有数十个不同的值。在这种情况下,我们可以使用系之间联系的知识,将系合并成较大的组,如工程学、社会科学或生物科学。
2.3.7变量变换
变量变换(variable transformation〉是指用于变量的所有值的变换。(尽管我们也偶尔用属性变换这个术语,但是遵循习惯用法,我们使用变量指代属性。)
讨论两种重要的变量变换类型:简单函数变换和规范化。
1.简单函数
对于这种类型的变量变换,一个简单数学函数分别作用于每一个值。如果x是变量,这种变换的例子包括
为了帮助弄清楚一个变换的效果,重要的是要问如下问题:需要保序吗?变换作用于所有的值,特别是负值和О吗?变换对0和1之间的值有何特别影响?本章习题17考察了变量变换的其他方面。
2.规范化或标准化
另一种常见的变量变换类型是变量的标准化(standardization)或规范化(norinalization)。
在数据挖掘界,这两个术语常常可互换,然而,在统计学中,术语规范化可能与使变量正态(高斯)的变换相混淆。
标准化或规范化的目标是使整个值的集合具有特定的性质。
均值和标准差受离群点的影响很大,因此通常需要修改上述变换。
首先,用中位数(median)即中间值)取代均值。其次,用绝对标准差(absolute standard deviation)取代标准差。
2.4相似性和相异性的度量
使用术语邻近度(proximity〉表示相似性或相异性。由于两个对象之间的邻近度是两个对象对应属性之间的邻近度的函数
2.4.1基础
1.定义
两个对象之间的相似度(similarity)的非正式定义是这两个对象相似程度的数值度量。因而,两个对象越相似,它们的相似度就越高。通常,相似度是非负的,并常常在0(不相似)和1(完全相似)之间取值。
两个对象之间的相异度(dissimilarity)是这两个对象差异程度的数值度量。对象越类似,它们的相异度就越低。通常,术语距离(distance)用作相异度的同义词
2.变换
通常使用变换把相似度转换成相异度或相反,或者把邻近度变换到一个特定区间
通常,邻近度度量(特别是相似度)被定义为或变换到区间[0,1]中的值。这样做的动机是使用一种适当的尺度,由邻近度的值表明两个对象之间的相似(或相异)程度。
2.4.2 简单属性之间的相似度和相异度
通常,具有若干属性的对象之间的邻近度用单个属性的邻近度的组合来定义
序数属性的相似度可以定义为s = 1 - d。
对于区间或比率属性,两个对象之间的相异性的自然度量是它们的值之差的绝对值。
表2-7总结了这些讨论。在该表中,x和y是两个对象,它们具有一个指明类型的属性, dx, y)和s(x, y)分别是x和y之间的相异度和相似度(分别用d和s表示)。其他方法也是可能的,但是表中的这些是最常用的。

2.4.3数据对象之间的相异度
本节讨论各种不同类型的相异度。从讨论距离(距离是具有特定性质的相异度)开始,然后给出一些更一般的相异度类型的例子。
距离
我们首先给出一些例子,然后使用距离的常见性质更正式地介绍距离。一维、二维、三维或高维空间中两个点x和y之间的欧几里得距离(Euclidean distance) d由如下熟悉的公式定义:

其中,n是维数,而和y分别是x和y的第k个属性值(分量)。


满足以上三个性质的测度称为度量(metric)。有些人只对满足这三个性质的相异性度量使用术语距离,但在实践中常常违反这一约定。
非度量的相异度:集合差
非度量的相异度:时间

2.4.4数据对象之间的相似度
对于相似度,三角不等式(或类似的性质)通常不成立,但是对称性和非负性通常成立。
更明确地说,如果s(x, y)是数据点x和y之间的相似度,则相似度具有如下典型性质。
(1)仅当x=y时s(x, y)= 1。(0≤s≤1)
(2)对于所有x和y,s(x, y)= s(y, x)。(对称性)
2.4.5邻近性度量的例子
1.二元数据的相似性度量
两个仅包含二元属性的对象之间的相似性度量也称为相似系数(similarity coefficient),并且通常在О和1之间取值,值为1表明两个对象完全相似,而值为О表明对象一点也不相似。
有许多理由表明在特定情形下,一种系数为何比另一种好。
设x和y是两个对象,都由n个二元属性组成。这样的两个对象(即两个二元向量》的比较可生成如下四个量(频率):



2.余弦相似度
通常,文档用向量表示,向量的每个属性代表一个特定的词〈术语)在文档中出现的频率。
尽管文档具有数以百千计或数以万计的属性(词),但是每个文档向量都是稀疏的,因为它具有相对较少的非零属性值。(文档规范化并不对零词目创建非零词目,即文档规范化保持稀疏性。)
这样,与事务数据一样,相似性不能依赖共享0的个数,因为任意两个文档多半都不会包含许多相同的词,从而如果统计0-0匹配,则大多数文档都与其他大部分文档非常类似。
因此,文档的相似性度量不仅应当像Jaccard度量一样需要忽略0-0匹配,而且还必须能够处理非二元向量。下面定义的余弦相似度〈cosine similarity)就是文档相似性最常用的度量之一。如果x和y是两个文档向量,则
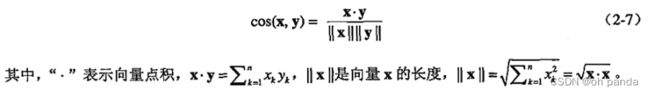


余弦相似度不考虑两个数据对象的量值。(当量值是重要的时,欧几里得距离可能是一种更好的选择。〉
对于长度为1的向量,余弦度量可以通过简单地取点积计算。从而,在需要计算大量对象之间的余弦相似度时,将对象规范化,使之具有单位长度可以减少计算时间。
3.广义Jaccard系数
广义Jaccard系数可以用于文档数据,并在二元属性情况下归约为Jaccard系数。
广义Jaccard系数又称Tanimoto系数。(然而,还有一种系数也称Tanimoto系数。)该系数用EJ表示,由下式定义:
![]()
4、相关性
两个具有二元变量或连续变量的数据对象之间的相关性是对象属性之间线性联系的度量。(更一般属性之间的相关性计算可以类似地定义。)
更准确地,两个数据对象x和y之间的皮尔森相关(Pearson’s correlation)系数由下式定义:


Bregman散度
Bregman 散度(Bregman divergence),它是一族具有共同性质的邻近函数。这样,可以构造使用Bregman 发散函数的一般数据挖掘算法,如聚类算法,具体的例子是K均值聚类算法(8.2节)。
Bregman 散度是损失或失真函数。为了理解损失函数,考虑如下情况:设x和y是两个点,其中y是原来的点,而x是它的某个失真或近似,例如,x可能是由于添加了一些随机噪声到y上而产生的。损失函数的目的是度量用x近似y导致的失真或损失。当然,x和y越类似,失真或损失就越小,因而Bregman散度可以用作相异性函数。

2.4.6邻近度计算问题
本节讨论与邻近性度量有关的一些重要问题:
(1)当属性具有不同的尺度(scale)或相关时如何处理;
(2)当对象包含不同类型的属性(例如,定量属性和定性属性〉时如何计算对象之间的邻近度;
(3)当属性具有不同的权重(即并非所有的属性都对对象的邻近度具有相等的贡献)时,如何处理邻近度计算。
1.距离度量的标准化和相关性
距离度量的一个重要问题是当属性具有不同的值域时如何处理。(这种情况通常称作“变量具有不同的尺度。”)
使用欧几里得距离,基于年龄和收入两个属性来度量人之间的距离。除非这两个属性是标准化的,否则两个人之间的距离将被收入所左右。

2.组合异种属性的相似度
前面的相似度定义所基于的方法都假定所有属性具有相同类型。
当属性具有不同类型时,就需要更一般的方法。直截了当的方法是使用表2-7分别计算出每个属性之间的相似度,然后使用一种导致0和1之间相似度的方法组合这些相似度。
总相似度一般定义为所有属性相似度的平均值。
不幸的是,如果某些属性是非对称属性,这种方法效果不好。例如,如果所有的属性都是非对称的二元属性,则相似性度量先归结为简单匹配系数-一种对于二元非对称属性并不合适的度量。
处理该问题的最简单方法是:如果两个对象在非对称属性上的值都是0,则在计算对象相似度时忽略它们。类似的方法也能很好地处理遗漏值。

3.使用权值
在前面的大部分讨论中,所有的属性在计算邻近度时都会被同等对待。
但是,当某些属性对邻近度的定义比其他属性更重要时,我们并不希望这种同等对待的方式。
为了处理这种情况,可以通过对每个属性的贡献加权来修改邻近度公式。
如果权w的和为1,则公式(2-15)变成

2.4.7选取正确的邻近性度量
邻近性度量的类型应当与数据类型相适应。
对于许多稠密的、连续的数据,通常使用距离度量,如欧几里得距离等。
连续属性之间的邻近度通常用属性值的差来表示,并且距离度量提供了一种将这些差组合到总邻近性度量的良好方法。
尽管属性可能有不同的取值范围和不同的重要性,但这些问题通常都可以用前面介绍的方法处理。
对于稀疏数据,常常包含非对称的属性,通常使用忽略0-0匹配的相似性度量。
从概念上讲,这反映了如下事实:对于一对复杂对象,相似度依赖于它们共同具有的性质数目,而不是依赖于它们都缺失的性质数目。
在特殊的情况下,对于稀疏的、非对称的数据,大部分对象都只具有少量被属性描述的性质,因此如果考虑它们都不具有的性质的话,它们都高度相似。余弦、Jaccard和广义Jaccard度量对于这类数据是合适的。
数据向量还有一些其他特征需要考虑。
例如,假定对于比较时间序列感兴趣。如果时间序列的量值是重要的(例如,每个时间序列表示同一单位不同年份的总销售),则可以使用欧几里得距离。
如果时间序列代表不同的量(例如,血压和氧消耗量),通常需要确定时间序列是否具有相同的形状,而不是相同的量值,那么相关度可能更可取(使用考虑量和级的差异的内置规范化)。
第三章 探索数据
3.1 鸢尾花数据集
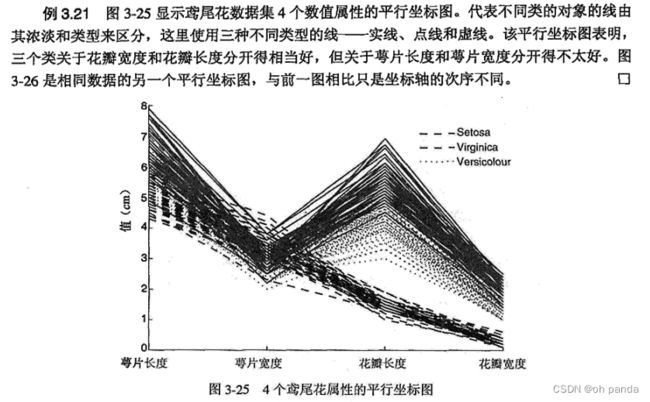
鸢尾花数据集包含150种鸢尾花的信息,每50种取自三个鸢尾花种之一:Setosa、Versicolour和 Virginica。每个花的特征用下面5种属性描述。
(1)萼片长度(厘米)。
(2)萼片宽度(厘米)。
(3花瓣长度厘米)。
(4)花瓣宽度(厘米)。
(5)类(Setosa,versicolour, Virginica)。
3.2 汇总统计
3.2.1频率和众数
3.2.2 百分位数
3.2.3 位置度量:均值和中位数
3.2.4散布度量:极差和方差
3.2.5 多元汇总统计

两个属性的协方差是两个属性一起变化并依赖于变量大小的度量。协方差的值接近于0表明两个变量不具有(线性)关系,但是不能仅靠观察协方差的值来确定两个变量之间的关联程度。因为两个属性的相关性直接指出两个属性(线性)相关的程度,对于数据探索,相关性比协方差更可取。


3.2.6 汇总数据的其他方法
当然,还有其他类型的汇总统计,例如,值集的倾斜度(skewness)度量值对称地分布在均值附近的程度。
另外还有一些其他数据特征,很难定量地度量,例如,值的分布是否是多模态的( multimodal),即数据具有多个“肿块”,大部分值集中在那里。
然而,在许多情况下,理解关于属性值如何分布的更复杂、更微妙的方面,最有效的方法是通过直方图观察这些值。(直方图在下一节讨论。
3.3 可视化
数据可视化是指以图形或表格的形式显示信息。
成功的可视化需要将数据(信息〕转换成可视的形式,以便能够借此分析或报告数据的特征和数据项或属性之间的关系。
可视化的目标是形成可视化信息的人工解释和信息的意境模型。
3.3.1可视化的动机
使用可视化技术的首要动机是人们能够快速吸取大量可视化信息,并发现其中的模式。
可视化的另一个动机是利用“锁在人脑袋中”的领域知识。
在某些情况下,可以使用非可视化工具进行分析,然后用可视化的方式提供结果,由领域专家进行评估。在其他情况下,让领域专家检查可视化数据可能是发现有意义的模式的最佳方法,因为利用领域知识,通常可以快速排除许多无意义的模式,并且直接聚焦到重要的模式上。
3.3.2 一般概念
1.表示:将数据映射到图形元素
可视化的第一步是将信息映射成可视形式,即将信息中的对象、属性和联系映射成可视的对象、属性和联系。也就是说,数据对象、它们的属性,以及数据对象之间的联系要转换成诸如点、线、形状和颜色等图形元素。
对象通常用三种方法表示。首先,如果只考虑对象的单个分类属性,则通常根据该属性的值将对象聚成类,并且把这些类作为表的项或屏幕的区域显示。
其次,如果对象具有多个属性,则可以将对象显示为表的一行(或列),或显示为图的一条线。最后,对象常常解释为二维或三维空间中的点,其中点可能用几何图形表示,如圆圈、十字叉或方框。
对于属性,其表示取决于属性的类型,即取决于属性是标称的、序数的还是连续的(区间的或比率的)。
序数的和连续的属性可以映射成连续的、有序的图形特征,如在x, y或z轴上的位置,亮度,颜色,或尺寸(直径、宽度或高度等)。
对于分类属性,每个类别可以映射到不同的位置、颜色、形状、方位、修饰物或表的列。
然而,对于标称属性,由于它的值是无序的,因此在使用具有与其值相关的囿有序的图形特征(如颜色、位置等)时,就需要特别小心。换言之,用来表示序数值的图形元素通常有序,但是标称值没有序。
可视化的主要难点是选择一种技术,让关注的联系易于观察。
2.安排
对于好的可视化来说,正确选择对象和属性的可视化表示是基本的要求。在可视化显示中,项的安排也是至关重要的。我们用两个例子解释这一点。

3.选择
可视化的另一个关键概念是选择(selection),即删除或不突出某些对象和属性。
具体说来,尽管只具有少数维的数据对象通常可以使用直截了当的方法映射成二维或三维图形表示,但是还没有令人完全满意和一般的方法表示具有许多属性的数据。同样,如果有很多数据对象,则可视化所有对象可能导致显示过于拥挤。如果有许多属性和许多对象,则情况会更加复杂。
处理很多属性的最常用方法是使用属性子集(通常是两个属性)。
如果维度不太高,则可以构造双变量(双属性)图矩阵用于联合观察。(图3-16显示鸢尾花数据集属性对的散布图矩阵。)或者说,可视化程序可以自动地显示一系列二维图,其中次序由用户或根据某种预定义的策略控制,让可视化二维图的集族提供数据的更完全的视图。
3.3.3技术
下面的讨论将使用三种类型:少量属性的可视化,具有时间和/或空间属性的数据可视化,以及具有大量属性的数据可视化。
1.少量属性的可视化


![]()


直方图有一些变形。相对频率直方图(relative frequency histogram)用相对频率取代计数,
然而,这只是一种y轴尺度的变化,直方图的形状并不改变。
另一种常见的变形是Pareto直方图(Pareto histogram),它专门针对无序的分类数据,Pareto直方图与普通直方图一样,只是分类按计数排序,让计数从左到右递减。

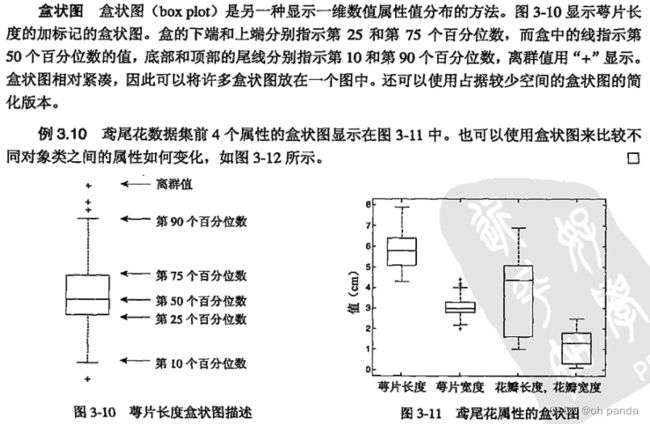

百分位数图和经验累计分布函数
一种更定量地显示数据分布的图是经验累计分布函数图。尽管这种类型的图听上去可能很复杂,但是概念相当简单。
对于统计分布的每个值,一个累计分布函数(cumulative distribution function,CDF)显示点小于该值的概率。
对于每个观测值,一个经验累计分布函数(empirical cumulative distribution function,ECDF)显示小于该值的点的百分比。由于点的个数是有限的,经验累计分布函数是一个阶梯函数。


散布图有两个主要用途。其一,它们图形化地显示两个属性之间的关系。在2.4.5节,我们看到如何使用散布图判定线性相关程度。直接使用散布图,或者使用变换后属性的散布图,也可以判定非线性关系。
其二,当类标号给出时,可以使用散布图考察两个属性将类分开的程度。如果可以画一条直线(或一条更复杂的曲线)将两个属性定义的平面分成区域,每个区域包含一个类的大部分对象,则可能基于这对指定的属性构造精确的分类器;否则的话,就需要更多的属性或更复杂的方法建立分类器。
在图3-16 中,许多属性对(例如,花瓣宽度和花瓣长度)都提供了适度的鸢尾花种类分隔。

扩展的二维和三维图
如图3-18所示,可以扩展成二维或三维图,以便提供一些附加的属性。
例如,使用颜色或阴影、大小、形状,散布图可以显示三个附加信息,可以表达五个或六个维。
然而,需要小心,随着数据可视表达的复杂性增加,对于解释信息的人就变得更加困难。将六个维的信息放进二维或三维图中没有多少好处,如果做的话也不可能理解。
2.可视化时间空间数据
等高线图
对于某些三维数据,两个属性指定平面上的位置,而第三个属性具有连续值,如温度或海拔高度。
对于这样的数据,一种有用的可视化工具是等高线图〈contour plot)。等高线图将平面划分成一些区域,区域中的第三个属性(温度或海拔高度〉的值粗略地相等。等高线图的常见例子是显示地面位置海拔高度的等高线图。
曲面图
与等高线图一样,曲面图〈surface plot〉使用两个属性表示x和y坐标,曲面图的第三个属性用来指示高出前两个属性定义的平面的高度。
尽管这种图可能是有用的,但是这要求至少某个范围内,对于前两个属性值的所有组合,第三个属性的值都有定义。此外,如果曲面不太规则,除非交互地观察,否则很难看到所有信息。因而,曲面图通常用来描述数学函数,或变化相对光滑的物理曲面。
矢量场图
在某些数据中,一个特性可能同时具有值和方向。例如,考虑物质流或随位置改变的密度。在这些情况下,同时显示方向和量的图可能是有用的。这种类型的图称作矢量图(vector plot)。
低维切片
考虑时间空间数据集,它记录不同地点和时间上的某种量,如温度或气压。这样的数据有四个维,不容易用迄今所介绍的图来显示。然而,通过显示一组图,每月一个,可以显示数据的各个“切片”。通过考察特定区域的逐月改变,就可能注意到所出现的变化,包括可能因为季节原因而导致的变化。
动画
无论是否涉及时间,处理数据切片的另一种方法是使用动画,其基本思想是显示数据的相继二维切片。人的视觉系统很适合检测视觉变化,并且常常能够注意到可能很难用其他方式检测到的变化。尽管动画具有视觉吸引力,但是一-组静止的图(如图3-22中的那些)可能更有用,因为这种类型的可视化使得我们可以按任意次序、使用任意多时间来研究这些信息。
3.3.4 可视化高维数据
本节介绍可以显示更多维的可视化技术,这些技术也有一些局限性:它们只能显示数据的某些侧面。
矩阵
图像可以看作像素的矩形阵列,其中每个像素用它的颜色和亮度刻画,数据矩阵是值的矩形阵列,那么,将数据矩阵的每个元素与图像中的一个像素相关联,就可以把数据矩阵看作图像,像素的亮度和颜色由矩阵对应元素的值决定。
在对数据矩阵可视化时,有一-些重要的实用性考虑:如果类标号已知,则重新排列数据矩阵的次序,使得某个类的所有对象聚在一起,这是很有用的方法,例如,这可以很容易地检查某个类的所有对象是否在某些属性上具有相似的属性值:如果不同的属性具有不同的值域,则可以对属性标准化,使其均值为0,标准差为1,这防止具有最大量值的属性在视觉上左右图形。
平行坐标系
平行坐标系(parallel coordinates)每个属性-一个坐标轴,但是与传统的坐标系不同,平行坐标系不同的坐标轴是平行的,而不是正交的。
对象用线而不是用点表示,具体地说,对象每个属性的值映射到与该属性相关联的坐标轴上的点,然后将这些点连接起来形成代表该对象的线。
星形坐标(star coordinates)
该技术对每个属性使用一个坐标轨,这些坐标轴从一个中心点向四周辐射,就像车轮的辐条,均匀地散开。通常,所有的属性值都映射到[0,1]区间。
使用如下过程将对象映射到星形坐标系:
将对象的每个属性值转换成一个分数,代表它在该属性的最大和最小值之间的距离,把这个分数映射到对应于该属性的坐标上的点,再将每个点用线段连接到相邻坐标轴上的点,形成一个多边形,多边形的大小和形状提供了对象属性值的视觉描述。为了便于解释,每个对象都使用单独的坐标系,换句话说,每个对象映射成一个多边形。星形坐标图的-一个例子是鸢尾花150号花的星形坐标图,如图3-27a所示。
还可以将特征值映射到更为熟悉的对象,如脸。
该技术以其创建者Herman Chernoff 的名字命名为Chernoff 脸(Chernoff face)。在这种技术中,每个属性与脸部的一个特征相关联,而属性的值确定脸部特征的表达方式。这样,随着对应的数据特征值的增加,脸的形状可能拉长。Chernoff 脸的一个例子是鸢尾花150号花的 Chernoff脸,如图3-27b所示。
用于将脸映射到4个特征的方案在下面列出。脸部的其他特征,如眼间宽度和口的长度,是给定的省缺值。
3.3.5注意事项
下面给出可视化注意事项的简短列表,以结束本节关于可视化的讨论。尽管这些指南颇具智慧,但也不能盲目遵循,指南永远不能取代对手头问题的深思熟虑。
ACCENT原则。下面是D.A. Burn 提出(经 Michael Friendly 改编〉的有效图形显示的ACCENT原则。
理解(Apprehension)。正确察觉变量之间关系的能力。图形能够最大化对变量之间关系
的理解吗?
清晰性(Clarity)。以目视识别图形中所有元素的能力。最重要的元素或关系在视觉上最突出吗?
一致性(Consistency)。根据与以前的图形的相似性解释图形的能力。元素、符号形状和颜色与以前图形使用的一致吗?
·有效性(Efficiency)。用尽可能简单的方法描绘复杂关系的能力。图形元素的使用经济吗?图形容易解释吗?
必要性(Necessity)。对图形和图形元素的需要。与其他替代方法(表、文本)相比,图形是提供数据的更有用的形式吗﹖为表示关系,所有的图形元素都是必要的吗?
真实性〈Truthfulness)。通过图形元素相对于隐式或显式尺度的大小,确定图形元素所代表的真实值的能力。图形元素可以准确地定位和定标吗?
Tufte指南。Edward R. Tufte列举了如下图形的优点(graphical excellence)原则。·图形的优点是感兴趣的(物质的、统计的和设计的)数据的良好设计的表示。图形的优点包括与清晰性、精确性和有效性相关的复杂思想。
图形的优点是它在最小的空间内、以最少的笔墨、在最短的时间内为观察者提供最多的信息。
图形的优点几乎总是多元的。
图形的优点需要表述数据的真实性。
3.4 OLAP和多维数据分析
3.4.1用多维数组表示鸢尾花数据
3.4.2多维数据:一般情况
开始通常使用表的形式表示数据(如表3-7),这种表称作事实表(fact table)。
用多维数组表示数据需要两个步骤:维的识别和分析所关注的属性的识别。
维是分类属性,或者如前面的例予所示,是转换成分类属性的连续属性。属性值充当对应于该属性的维的数组下标,而属性值的个数是维的大小。
在前面的例子中,每个属性有三个可能的值,因此每个维的大小都是3,并且可以通过3个值索引。这产生了3×3×3的多维数组。
属性值的每个组合(每个不同的属性一个值)定义了多维数组的一个单元。使用前面的例子解释,如果花瓣长度=低,花瓣宽度= 中,而种类=Setosa,则标识了一个值为2的特定单元。即,数据集中只有两种花具有指定的属性值。注意,表3-7中数据集的每一行(对象)对应于多维数组的一个单元。
每个单元的内容代表一个我们在分析时感兴趣的目标量(target quantity)(目标变量或属性)的值。在鸢尾花例子中,目标量是其花瓣宽度和长度落入特定范围内的花的个数。目标属性是定量的,因为多维数据分析的关键目标是观察聚集量,如总和或平均值。
总结用表形式表示的数据集创建多维数据表示的过程:
首先确定用作维的分类属性以及用作分析目标的定量属性,然后将表的每一行(对象〉映射到多维数组的一个单元,单元的下标由被选作维的属性的值指定,而单元的值是目标属性的值,假定没有被数据定义的单元的值为0。
3.4.3分析多维数据
本节介绍不同的多维分析技术。重点讨论数据立方体的创建和相关操作,如切片、切块、维归约、上卷和下钻。
1.数据立方体:计算聚集量
从多维角度看待数据的主要动机就是需要以多种方式聚集数据。

数据的多维表示,连同所有可能的总和(聚集)称作数据立方体(data cube)。尽管叫立方体,每个维的大小(属性值的个数)却不必相等。此外,数据立方体可能多于或少于三个维。
2.维归约和转轴
转轴(pivoting)是指在除两个维之外的所有维上聚集。结果是一个二维交叉表,只有两个指定的维作为留下的维。表3-13是一个在日期和产品上转轴的例子。
3.切片和切块
切片(slicing)是通过对一个或多个维指定特定的值,从整个多维数组中选择一组单元。
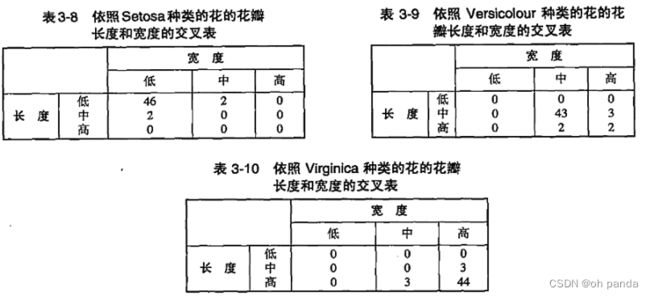
表3-8、表3-9和表3-10是通过为种类维指定三个不同的值得到的鸢尾花数据集的三个切片。
切块(dicing)涉及通过指定属性值区间选择单元子集,这等价于由整个数组定义子数组。
4.上卷和下钻
层次结构促使上卷和下钻操作的出现。
为了解释这一点,考虑最初的销售数据,它是多维数组,记录每天的销售。
我们可以按月聚集(上卷,roll up)销售数据。反过来,给定时间为划分成月份的数据表示,我们可能希望将月销售总和分解(下钻,drill down)成日销售总和,当然,这要求基本销售数据的时间粒度是按天的。
这样,上卷和下钻操作与聚集相关。它们在一个维内聚集单元,而不是在整个维上聚集。
第四章 分类:基本概念、决策树与模型评估
分类任务就是确定对象属于哪个预定义的目标类。
4.1预备知识
分类任务的输入数据是记录的集合。每条记录也称实例或样例,用元组(x, y)表示,其中x是属性的集合,而y是一个特殊的属性,指出样例的类标号(也称为分类属性或目标属性)。
属性集也可以包含连续特征。另一方面,类标号却必须是离散属性,这正是区别分类与回归(regression)的关键特征。
回归是一种预测建模任务,其中目标属性y是连续的。
定义4.1 分类(classification)
分类任务就是通过学习得到-一个目标函数(target function)f把每个属性集x映射到一个预先定义的类标号y。
目标函数也称分类模型(classification model)。分类模型可以用于以下目的。
描述性建模 分类模型可以作为解释性的工具,用于区分不同类中的对象。
预测性建模分类模型还可以用于预测未知记录的类标号。
分类技术非常适合预测或描述二元或标称类型的数据集,对于序数分类(例如,把人分类为高收入、中等收入或低收入组),分类技术不太有效,因为分类技术不考虑隐含在目标类中的序关系。
4.2 解决分类问题的一般方法
分类技术(或分类法)是一种根据输入数据集建立分类模型的系统方法。
分类法的例子包括决策树分类法、基于规则的分类法、神经网络、支持向量机和朴素贝叶斯分类法。
这些技术都使用一种学习算法(learning algorithm)确定分类模型,该模型能够很好地拟合输入数据中类标号和属性集之间的联系。
学习算法得到的模型不仅要很好地拟合输入数据,还要能够正确地预测未知样本的类标号。因此,训练算法的主要目标就是建立具有很好的泛化能力模型,即建立能够准确地预测未知样本类标号的模型。


4.3决策树归纳
4.3.1决策树的工作原理
通过提出一系列精心构思的关于检验记录属性的问题,可以解决分类问题。每当一个问题得到答案,后续的问题将随之而来,直到我们得到记录的类标号。
这一系列的问题和这些问题的可能回答可以组织成决策树的形式,决策树是一种由结点和有向边组成的层次结构。图4-4显示哺乳类动物分类问题的决策树,树中包含三种结点。
根结点(root node),它没有入边,但有零条或多条出边。
内部结点〈internal node),恰有一条入边和两条或多条出边。
叶结点(leaf node)或终结点(terminal node),恰有一条入边,但没有出边。
在决策树中,每个叶结点都赋予一个类标号。非终结点(non-terminal node)(包括根结点和内部结点)包含属性测试条件,用以分开具有不同特性的记录。

4.3.2如何建立决策树
原则上讲,对于给定的属性集,可以构造的决策树的数目达指数级。
尽管某些决策树比其他决策树更准确,但是由于搜索空间是指数规模的,找出最佳决策树在计算上是不可行的。
尽管如此,人们还是开发了一些有效的算法,能够在合理的时间内构造出具有一定准确率的次最优决策树。
这些算法通常都采用贪心策略,在选择划分数据的属性时,采取一系列局部最优决策来构造决策树,Hunt算法就是一种这样的算法。Hunt算法是许多决策树算法的基础,包括D3、C4.5和CART。
1.Hunt算法
2.决策树归纳的设计问题
决策树归纳的学习算法必须解决下面两个问题。
(1)如何分裂训练记录?树增长过程的每个递归步都必须选择一个属性测试条件,将记录划分成较小的子集。为了实现这个步骤,算法必须提供为不同类型的属性指定测试条件的方法,并且提供评估每种测试条件的客观度量。
(2)如何停止分裂过程?需要有结束条件,以终止决策树的生长过程。一个可能的策略是分裂结点,直到所有的记录都属于同一个类,或者所有的记录都具有相同的属性值。尽管两个结束条件对于结束决策树归纳算法都是充分的,但是还可以使用其他的标准提前终止树的生长过程。
4.3.3表示属性测试条件的方法
决策树归纳算法必须为不同类型的属性提供表示属性测试条件和其对应输出的方法。
二元属性二元属性的测试条件产生两个可能的输出,如图4-8所示。


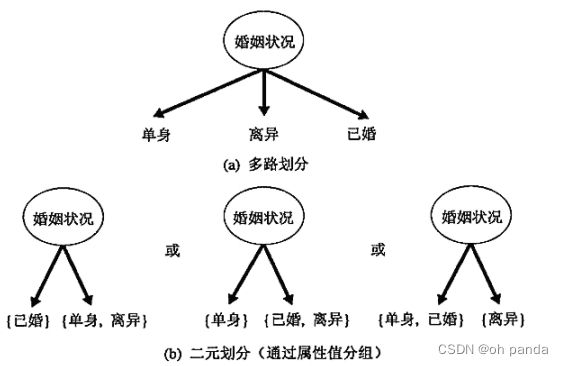
序数属性
序数属性也可以产生二元或多路划分,只要不违背序数属性值的有序性,就可以对属性值进行分组。
图4-10显示了按照属性衬衣尺码划分训练记录的不同的方法。图4-10a和图4-10b 中的分组保持了属性值间的序关系,而图4-10c 所示的分组则违反了这一性质,因为它把小号和大号分为一组,把中号和加大号放在另一组。


4.3.4选择最佳划分的度量
1.二元属性的划分
2.标称属性的划分
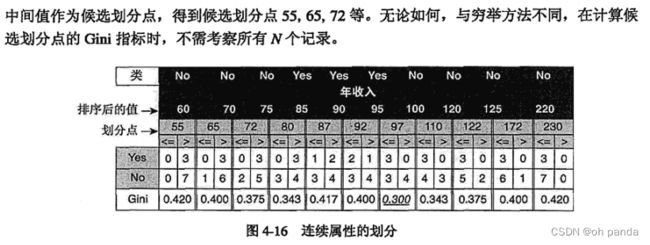
3.连续属性的划分
4.增益率
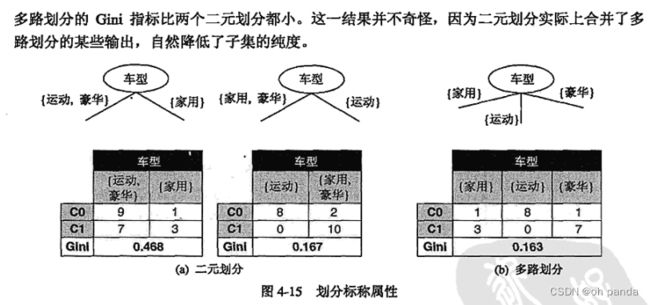
嫡和Gini指标等不纯性度量趋向有利于具有大量不同值的属性。
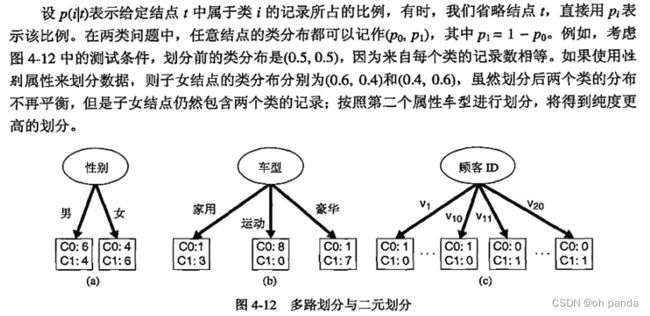
图4-12显示了三种可供选择的测试条件,划分本章习题2中的数据集。第一个测试条件性别与第二个测试条件车型相比,容易看出车型似乎提供了更好的划分数据的方法,因为它产生更纯的派生结点。
然而,如果将这两个条件与顾客D相比,后者看来产生更纯的划分,但顾客D却不是一个有预测性的属性,因为每个样本在该属性.上的值都是唯一的。
即使在不太极端情形下,也不会希望产生大量输出的测试条件,因为与每个划分相关联的记录太少,以致不能作出可靠的预测。
解决该问题的策略有两种。第一种策略是限制测试条件只能是二元划分,CART 这样的决策树算法采用的就是这种策略;
另一种策略是修改评估划分的标准,把属性测试条件产生的输出数也考虑进去,例如,决策树算法C4.5采用称作增益率(gain ratio)的划分标准来评估划分。增益率定义如下:


4.3.5决策树归纳算法


建立决策树之后,可以进行树剪枝(tree-pruning),以减小决策树的规模。决策树过大容易受所谓过分拟合(overfitting)现象的影响。
4.3.6例子: Web机器人检测
4.3.7决策树归纳的特点
(1)决策树归纳是一种构建分类模型的非参数方法。换句话说,它不要求任何先验假设,不假定类和其他属性服从一定的概率分布
(2)找到最佳的决策树是NP完全问题。许多决策树算法都采取启发式的方法指导对假设空间的搜索。
(3)已开发的构建决策树技术不需要昂贵的计算代价,即便训练集非常大,也可以快速建立模型。此外,决策树一旦建立,未知样本分类非常快,最坏情况下的时间复杂度是O(w),其中 w是树的最大深度。
(4)决策树相对容易解释,特别是小型的决策树。在很多简单的数据集上,决策树的准确率也可以与其他分类算法相媲美。

(6)决策树算法对于噪声的干扰具有相当好的鲁棒性,采用避免过分拟合的方法之后尤其如此。
(7)冗余属性不会对决策树的准确率造成不利的影响。
(8)由于大多数的决策树算法都采用自顶向下的递归划分方法,因此沿着树向下,记录会越来越少。在叶结点,记录可能太少,对于叶结点代表的类,不能做出具有统计意义的判决,这就是所谓的数据碎片(data fragmentation)问题。
(9)子树可能在决策树中重复多次
(10)迄今为止,本章介绍的测试条件每次都只涉及一个属性。这样,可以将决策树的生长过程看成划分属性空间为不相交的区域的过程,直到每个区域都只包含同一类的记录(见图4-20)。两个不同类的相邻区域之间的边界称作决策边界(decision boundary)。由于测试条件只涉及单个属性,因此决策边界是直线,即平行于“坐标轴”,这就限制了决策树对连续属性之间复杂关系建模的表达能力。图4-21显示了一个数据集,使用一次只涉及一个属性的测试条件的决策树算法很难有效地对它进行分类。
![]()
斜决策树(oblique decision tree)可以克服以上的局限,因为它允许测试条件涉及多个属性。图4-21中的数据集可以很容易地用斜决策树表示,该斜决策树只有一个结点,其测试条件为:
x +y< 1
构造归纳(constructive induction)提供另一种将数据划分成齐次非矩形区域的方法(见2.3.5节),该方法创建复合属性,代表已有属性的算术或逻辑组合。
新属性提供了更好的类区分能力,并在决策树归纳之前就增广到数据集中。与斜决策树不同,构造归纳不需要昂贵的花费,因为在构造决策树之前,它只需要一次性地确定属性的所有相关组合。
相比之下,在扩展每个内部结点时,斜决策树都需要动态地确定正确的属性组合。然而,构造归纳会产生冗余的属性,因为新创建的属性是已有属性的组合。
4.4模型的过分拟合
分类模型的误差大致分为两种:训练误差(training error)和泛化误差(generalization error)。
训练误差也称再代入误差(resubstitution error)或表现误差( apparent error),是在训练记录上误分类样泛化误差是模型在未知记录上的期望误差。
一个好的分类模型不仅要能够很好地拟合训练数据,而且对未知样本也要能准确地分类。
换句话说,一个好的分类模型必须具有低训练误差和低泛化误差。这一点非常重要,因为对训练数据拟合度过高的模型,其泛化误差可能比具有较高训练误差的模型高。这种情况就是所谓的模型过分拟合。
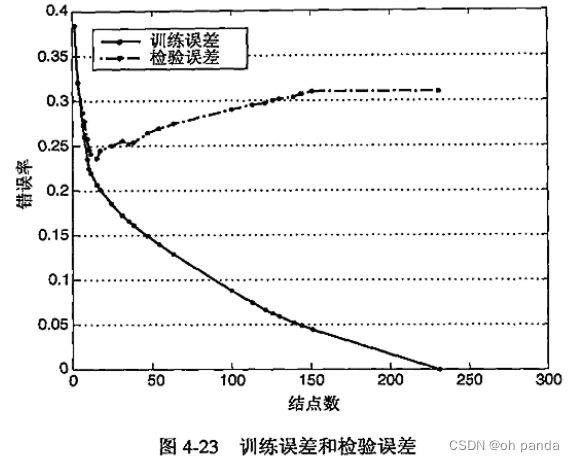
当决策树很小时,训练和检验误差都很大,这种情况称作模型拟合不足( modelunderfitting)。
出现拟合不足的原因是模型尚未学习到数据的真实结构,因此,模型在训练集和检验集上的性能都很差。随着决策树中结点数的增加,模型的训练误差和检验误差都会随之降低。
然而,一旦树的规模变得太大,即使训练误差还在继续降低,但是检验误差开始增大,这种现象称为模型过分拟合(model overfitting)。
4.4.1噪声导致的过分拟合
考虑表4-3和表4-4中哺乳动物的分类问题的训练数据集合和检验数据集合。十个训练记录中有两个被错误地标记:蝙蝠和鲸被错误地标记为非哺乳类动物,而不是哺乳类动物。



4.4.2缺乏代表性样本导致的过分拟合


人、大象和海豚都被误分类,因为决策树把恒温但不冬眠的脊柱动物划分为非哺乳动物。决策树做出这样的分类决策是因为只有一个训练记录(鹰)具有这些特性。这个例子清楚地表明,当决策树的叶结点没有足够的代表性样本时,很可能做出错误的预测。
4.4.3过分拟合与多重比较过程
模型的过分拟合可能出现在使用所谓的多重比较过程( multiple comparison procedure)的学习算法中。





4.4.4泛化误差估计
虽然过分拟合的主要原因-一直是个争辩的话题,大家还是普遍同意模型的复杂度对模型的过分拟合有影响,如图4-23所示。问题是,如何确定正确的模型复杂度?
理想的复杂度是能产生最低泛化误差的模型的复杂度。然而,在建立模型的过程中,学习算法只能访问训练数据集〈见图4-3),对检验数据集,它一无所知,因此也不知道所建立的决策树在未知记录上的性能。我们所能做的就是估计决策树的泛化误差。本节提供一些估计泛化误差的方法。
1.使用再代入估计
再代入估计方法假设训练数据集可以很好地代表整体数据,因而,可以使用训练误差(又称再代入误差)提供对泛化误差的乐观估计。
在这样的前提下,决策树归纳算法简单地选择产生最低训练误差的模型作为最终的模型。然而,训练误差通常是泛化误差的一种很差的估计。
2.结合模型复杂度
模型越是复杂,出现过分拟合的几率就越高,因此,我们更喜欢采用较为简单的模型。
这种策略与应用众所周知的奥卡姆剃刀(Occam’s razor)或节俭原则(principle of parsimony)一致。
定义4.2奥卡姆剃刀:给定两个具有相同泛化误差的模型,较简单的模型比较复杂的模型更可取。
下面我们介绍两种把模型复杂度与分类模型评估结合在一起的方法。
悲观误差评估
第一种方法明确使用训练误差与模型复杂度罚项(penalty term)的和计算泛化误差。
结果泛化误差可以看作模型的悲观误差估计((pessimistic error estimate)。
例如,设nkt)是结点 t分类的训练记录数,et是被误分类的记录数。决策树T的悲观误差估计eg(T)可以用下式计算:



3.估计统计上界
泛化误差也可以用训练误差的统计修正来估计。因为泛化误差倾向于比训练误差大,所以统计修正通常是计算训练误差的上界,考虑到达决策树一个特定叶结点的训练记录数。
例如,决策树算法C4.5中,假定每个叶结点上的错误服从二项分布。为了计算泛化误差,我们需要确定训练误差的上限,在下面的例子中解释说明。

4.使用确认集
在该方法中,不是用训练集估计泛化误差,而是把原始的训练数据集分为两个较小的子集,一个子集用于训练,而另一个称作确认集,用于估计泛化误差。典型的做法是,保留2/3的训练集来建立模型,剩余的1/3用作误差估计。
该方法常常用于通过参数控制获得具有不同复杂度模型的分类技术。通过调整学习算法中的参数(如决策树中剪枝的程度),直到学习算法产生的模型在确认集上达到最低的错误率,可以估计最佳模型的复杂度。虽然该方法为评估模型在未知样本上的性能提供了较好办法,但用于训练的记录减少了。
4.4.5处理决策树归纳中的过分拟合
先剪枝(提前终止规则)
在这种方法中,树增长算法在产生完全拟合整个训练数据集的完全增长的决策树之前就停止决策树的生长。
为了做到这一点,需要采用更具限制性的结束条件,例如,当观察到的不纯性度量的增益(或估计的泛化误差的改进〉低于某个确定的阙值时就停止扩展叶结点。
这种方法的优点在于避免产生过分拟合训练数据的过于复杂的子树,然而,很难为提前终止选取正确的阈值。阈值太高将导致拟合不足的模型,而阅值太低就不能充分地解决过分拟合的问题。
后剪枝
在该方法中,初始决策树按照最大规模生长,然后进行剪枝的步骤,按照自底向上的方式修剪完全增长的决策树。修剪有两种做法:
(1)用新的叶结点替换子树,该叶结点的类标号由子树下记录中的多数类确定;
(2)用子树中最常使用的分支代替子树。当模型不能再改进时终止剪枝步骤。与先剪枝相比,后剪枝技术倾向于产生更好的结果,因为不像先剪枝,后剪枝是根据完全增长的决策树做出的剪枝决策,先剪枝则可能过早终止决策树的生长。
然而,对于后剪支,当子树被剪掉后,生长完全决策树的额外的计算就被浪费了。
4.5评估分类器的性能
估计误差有助于学习算法进行模型选择(model selection),即找到一个具有合适复杂度、不易发生过分拟合的模型。模型一旦建立,就可以应用到检验数据集上,预测未知记录的类标号。
测试模型在检验集上的性能是有用的,因为这样的测量给出模型泛化误差的无偏估计。在检验集上计算出的准确率或错误率可以用来比较不同分类器在相同领域上的性能。然而,为了做到这一点,检验记录的类标号必须是已知的。本节回顾一些常用的评估分类器性能的方法。
4.5.1保持方法
在保持(Holdout)方法中,将被标记的原始数据划分成两个不相交的集合,分别称为训练集和检验集。在训练数据集上归纳分类模型,在检验集上评估模型的性能。训练集和检验集的划分比例通常根据分析家的判断。分类器的准确率根据模型在检验集上的准确率估计。
保持方法有一些众所周知的局限性。
第一,用于训练的被标记样本较少,因为要保留一部分记录用于检验,因此,建立的模型不如使用所有被标记样本建立的模型好。
第二,模型可能高度依赖于训练集和检验集的构成。一方面,训练集越小,模型的方差越大,另一-方面,如果训练集太大,根据用较小的检验集估计的准确率又不太可靠。这样的估计具有很宽的置信区间。最后,训练集和检验集不再是相互独立的。因为训练集和检验集来源于同一个数据集,在一个子集中超出比例的类在另一个子集就低于比例,反之亦然。
4.5.2随机二次抽样
4.5.3交叉验证
替代随机二次抽样的一种方法是交叉验证(cross-validation)。在该方法中,每个记录用于训练的次数相同,并且恰好检验一次。为了解释该方法,假设把数据分为相同大小的两个子集,首先,我们选择一个子集作训练集,而另一个作检验集,然后交换两个集合的角色,原先作训练集的现在做检验集,反之亦然,这种方法叫二折交叉验证。总误差通过对两次运行的误差求和得到。在这个例子中,每个样本各作–次训练样本和检验样本。
k折交叉验证是对该方法的推广,把数据分为大小相同的k份,在每次运行,选择其中一份作检验集,而其余的全作为训练集,该过程重复k次,使得每份数据都用于检验恰好一次。同样,总误差是所有k次运行的误差之和。k折交叉验证方法的一种特殊情况是令k = N,其中N是数据集的大小,在这种所谓留一(leave-one-out)方法中,每个检验集只有一个记录。该方法的优点是使用尽可能多的训练记录,此外,检验集之间是互斥的,并且有效地覆盖了整个数据集;该方法的缺点是整个过程重复Ⅳ次,计算上开销很大,此外,因为每个检验集只有一个记录,性能估计度量的方差偏高。
4.5.4自助法
4.6比较分类器的方法
比较不同分类器的性能,以确定在给定的数据集上哪个分类器效果更好是很有用的。但是,依据数据集的大小,两个分类器准确率上的差异可能不是统计显著的。本节介绍一些统计检验方法,可以用来比较不同模型和分类器的性能。

4.6.1估计准确度的置信区间
4.6.2比较两个模型的性能
4.6.3比较两种分类法的性能
第五章 分类:其他技术
本章讲述构建分类模型的其他技术—从最简单的基于规则的分类器和最近邻分类器到更高级的支持向量机和组合方法。其他重要问题,如类失衡和多类问题等,也在本章后面部分进行讨论。
5.1基于规则的分类器
5.1.1基于规则的分类器的工作原理
互斥规则〈Mutually Exclusive Rule)如果规则集R中不存在两条规则被同一条记录触发,则称规则集R中的规则是互斥的。
这个性质确保每条记录至多被R中的一条规则覆盖。表5-3是一个互斥规则集的例子。
穷举规则(Exhaustive Rule)如果对属性值的任一组合,R中都存在一条规则加以覆盖,则称规则集R具有穷举覆盖。
这个性质确保每一条记录都至少被R中的一条规则覆盖。假设体温和胎生是二元变量,则表5-3中的规则集具有穷举覆盖。
![]()

如果规则集不是互斥的,那么一条记录可能被多条规则覆盖,这些规则的预测可能会相互冲突。解决这个问题有如下两种方法。
有序规则(ordered rule)在这种方法中,规则集中的规则按照优先级降序排列,优先级的定义有多种方法(如基于准确率、覆盖率、总描述长度或规则产生的顺序等)。
有序的规则集也称为决策表〈decision list)。当测试记录出现时,由覆盖记录的最高秩的规则对其进行分类,这就避免由多条分类规则来预测而产生的类冲突的问题。
无序规则〈unordered rule)这种方法允许一条测试记录触发多条分类规则,把每条被触发规则的后件看作是对相应类的一次投票,然后计票确定测试记录的类标号。通常把记录指派到得票最多的类。
在某些情况下,投票可以用规则的准确率加权。使用无序规则来建立基于规则的分类器有利也有弊。
首先,无序规则方法在分类一个测试记录时,不易受由于选择不当的规则而产生的错误的影响(而基于有序规则的分类器则对规则排序方法的选择非常敏感)。
其次,建立模型的开销也相对较小,因为不必维护规则的顺序。然而,对测试记录进行分类却是一件很繁重的任务,因为测试记录的属性要与规则集中的每一条规则的前件作比较。
5.1.2规则的排序方案
对规则的排序可以逐条规则进行或者逐个类进行
基于规则的排序方案
这个方案依据规则质量的某种度量对规则排序。这种排序方案确保每一个测试记录都是由覆盖它的“最好的”规则来分类。该方案的潜在缺点是规则的秩越低越难解释,因为每个规则都假设所有排在它前面的规则不成立。
例如,图5-1左图基于规则的排序中第四条规则
![]()
基于类的排序方案
在这种方案中,属于同一个类的规则在规则集R中-一起出现。然后,这些规则根据它们所属的类信息一起排序。
同一个类的规则之间的相对顺序并不重要,只要其中一个规则被激发,类标号就会赋给测试记录。这使得规则的解释稍微容易一些。然而,质量较差的规则可能碰巧预测较高秩的类,从而导致高质量的规则被忽略。
5.1.3如何建立基于规则的分类器
为了建立基于规则的分类器,需要提取一组规则来识别数据集的属性和类标号之间的关键联系。提取分类规则的方法有两大类:(1)直接方法,直接从数据中提取分类规则:(2)间接方法,从其他分类模型(如决策树和神经网络〉中提取分类规则。
直接方法把属性空间分为较小的子空间,以便于属于一个子空间的所有记录可以使用一个分类规则进行分类。间接方法使用分类规则为较复杂的分类模型提供简洁的描述。5.1.4节和5.1.5节分别对这两种方法进行详细讨论。
5.1.4规则提取的直接方法
顺序覆盖(sequential covering)算法经常被用来直接从数据中提取规则,规则基于某种评估度量以贪心的方式增长。
该算法从包含多个类的数据集中一次提取一个类的规则。对于脊椎动物分类问题,顺序覆盖算法可能先产生对鸟类进行分类的规则,然后依次是哺乳类、两栖类、爬行类,最后是鱼类的分类规则(见图5-1)。决定哪一个类的规则最先产生的标准取决于多种因素,如类的普遍性(即训练记录中属于特定类的记录的比例),或者给定类中误分类记录的代价。
算法5.1给出顺序覆盖算法的描述。算法开始时决策表R为空。接下来用函数Learn-One-Rule提取类y的覆盖当前训练记录集的最佳规则。
在提取规则时,类y的所有训练记录被看作是正例,而其他类的训练记录则被当成反例。如果一个规则覆盖大多数正例,没有或仅覆盖极少数反例,那么该规则是可取的。
一旦找到这样的规则,就删掉它所覆盖的训练记录,并把新规则追加到决策表R的尾部。重复这个过程,直到满足终止条件。然后,算法继续产生下一个类的规则。
1.Learn-One-Rule函数
Learn-One-Rule函数的目标是提取一个分类规则,该规则覆盖训练集中的大量正例,没有或仅覆盖少量反例。然而,由于搜索空间呈指数大小,要找到一个最佳的规则的计算开销很大。
Learn-One-Rule 函数通过以一种贪心的方式的增长规则来解决指数搜索问题。
它先产生一个初始规则r,并不断对该规则求精,直到满足某种终止条件为止。然后,修剪该规则,以改进它的泛化误差。


规则评估
在规则增长过程中,需要一种评估度量来确定应该添加(或删除)哪个合取项。准确率就是一个很明显的选择,因为它明确地给出了被规则正确分类的训练样例的比例。然而,把准确率作为标准的一个潜在的局限性是它没有考虑规则的覆盖率。
例如,考虑一个训练集,它包含60个正例和100个反例。假设有如下两个候选规则。
2.顺序覆盖基本原理
3.RiPPER算法
规则增长
RIPPER 算法使用从一般到特殊的策略进行规则增长,使用FOIL信息增益来选择最佳合取项添加到规则前件中。当规则开始覆盖反例时,停止添加合取项。新规则根据其在确认集上的性能进行剪枝。
计算下面的度量来确定规则是否需要剪枝:(p- n)/(p + n),其中p和n分别是被规则覆盖的确认集中的正例和反例数目,关于规则在确认集上的准确率,该度量是单调的。如果剪枝后该度量值增加,那么就去掉该合取项。剪枝是从最后添加的合取项开始的。例如,给定规则ABCD -> y,RIPPER算法先检查D是否应该剪枝,然后是CD、BCD等。尽管原来的规则仅覆盖正例,但是剪枝后的规则可能会覆盖训练集中的一些反例。
建立规则集
规则生成后,它所覆盖的所有正例和反例都要被删除。只要该规则不违反基于最小描述长度原则的终止条件,就将它添加到规则集中。
如果新规则把规则集的总描述长度增加了至少d个比特位,那么RTPPER就停止把该规则加入到规则集(默认的d是64位)。RIPPER使用的另一个终止条件是规则在确认集上的错误率不超过50%。
5.1.5规则提取的间接方法
本节介绍一种由决策树生成规则集的方法。原则上,决策树从根结点到叶结点的每一条路径都可以表示为一个分类规则。
路径中的测试条件构成规则前件的合取项,叶结点的类标号赋给规则后件。图5-5显示了一个由决策树生成规则集的例子。注意,规则集是完全的,包含的规则是互斥的。但是,如下面的例子所示,其中某些规则可以加以简化。




5.1.6基于规则的分类器的特征
规则集的表达能力几乎等价于决策树,因为决策树可以用互斥和穷举的规则集表示。基于规则的分类器和决策树分类器都对属性空间进行直线划分,并将类指派到每个划分。然而,如果基于规则的分类器允许一条记录触发多条规则的话,就可以构造一个更加复杂的决策边界。
基于规则的分类器通常被用来产生更易于解释的描述性模型,而模型的性能却可与决策树分类器相媲美。
被很多基于规则的分类器(如RIPPER〉所采用的基于类的规则定序方法非常适于处理类分布不平衡的数据集。
5.2最近邻分类器
图4-3中显示的分类框架包括两个步骤:
(1)归纳步,由训练数据建立分类模型;
⑵演绎步,把模型应用于测试样例。决策树和基于规则的分类器是积极学习方法(eager learner)的例子,因为如果训练数据可用,它们就开始学习从输入属性到类标号的映射模型。
与之相反的策略是推迟对训练数据的建模,直到需要分类测试样例时再进行。采用这种策略的技术被称为消极学习方法(lazy learner)。
消极学习的一个例子是Rote分类器(Rote classifier),它记住整个训练数据,仅当测试实例的属性和某个训练样例完全匹配时才进行分类。该方法–个明显的缺点是有些测试记录不能被分类,因为没有任何训练样例与它们相匹配。


5.2.1算法
5.2.2最近邻分类器的特征
5.3贝叶斯分类器
在很多应用中,属性集和类变量之间的关系是不确定的。换句话说,尽管测试记录的属性集和某些训练样例相同,但是也不能正确地预测它的类标号。这种情况产生的原因可能是噪声,或者出现了某些影响分类的因素却没有包含在分析中。
例如,考虑根据一个人的饮食和锻炼的频率来预测他是否有患心脏病的危险。尽管大多数饮食健康、经常锻炼身体的人患心脏病的机率较小,但仍有人由于遗传、过量抽烟、酗酒等其他原因而患病。确定一个人的饮食是否健康、体育锻炼是否充分也是需要论证的课题,这反过来也会给学习问题带来不确定性。
本节将介绍一种对属性集和类变量的概率关系建模的方法。首先介绍贝叶斯定理(Bayestheorem),它是一种把类的先验知识和从数据中收集的新证据相结合的统计原理;然后解释贝叶斯定理在分类问题中的应用,接下来描述贝叶斯分类器的两种实现:朴素贝叶斯和贝叶斯信念网络。
5.3.1贝叶斯定理
5.3.2贝叶斯定理在分类中的应用
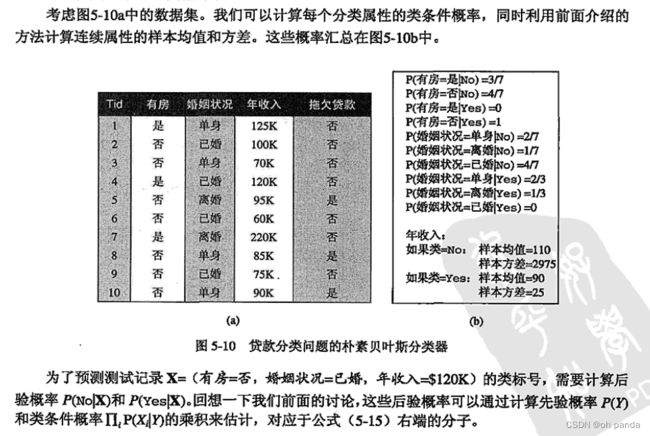
5.3.3 .朴素贝叶斯分类器
5.朴素贝叶斯分类器举例
6.条件概率的m估计
7.朴素贝叶斯分类器的特征
5.3.4贝叶斯误差率
假设我们知道支配P(X|Y)的真实概率分布。使用贝叶斯分类方法,我们就能确定分类任务的理想决策边界,如下例所示。


5.3.5贝叶斯信念网络
朴素贝叶斯分类器的条件独立假设似乎太严格了,特别是对那些属性之间有~一定相关性的分类问题。本节介绍一种更灵活的类条件概率P(X|P)的建模方法。该方法不要求给定类的所有属性都条件独立,而是允许指定哪些属性条件独立。我们先讨论怎样表示和建立该概率模型,接着举例说明怎样使用模型进行推理。


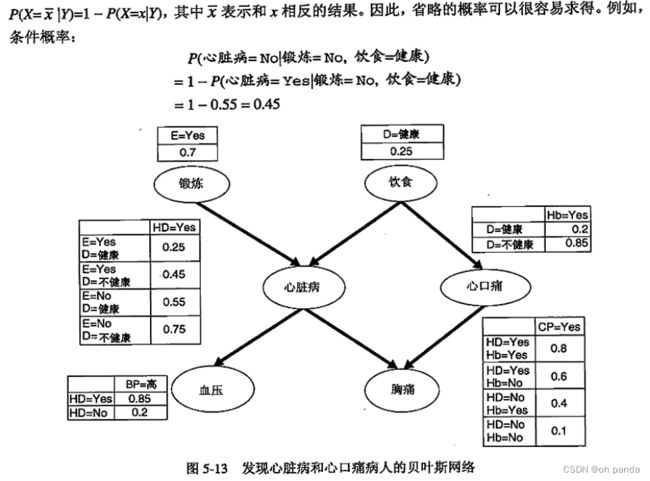






5.4人工神经网络
5.4.1感知器
学习感知器模型
在感知器模型的训练阶段,权值参数w不断调整直到输出和训练样例的实际输出一致。算法5.4中给出了感知器学习算法的概述。


在权值更新公式中,对误差项影响最大的链需要的调整最大。然而,权值不能改变太大,因为仅仅对当前训练样例计算了误差项。否则的话,以前的循环中所作的调整就会失效。学习率其值在О和1之间,可以用来控制每次循环时的调整量。如果2接近0,那么新权值主要受旧权值的影响;相反,如果3接近1,则新权值对当前循环中的调整量更加敏感。在某些情况下,可以使用一个自适应的3值;X在前几次循环时值相对较大,而在接下来的循环中逐渐减小。

5.4.2多层人工神经网络
人工神经网络结构比感知器模型更复杂。这些额外的复杂性来源于多个方面。
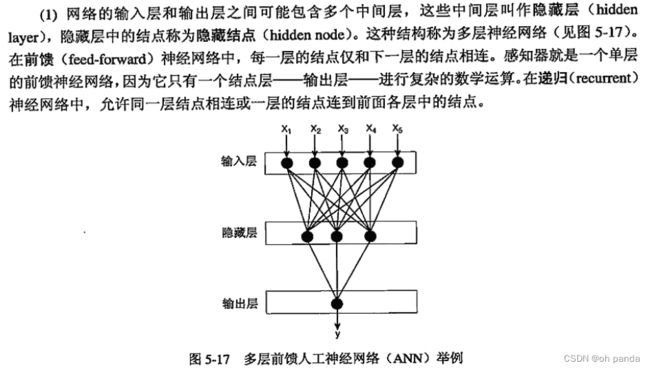


1.学习ANN模型
2.ANN学习中的设计问题
在训练神经网络来学习分类任务之前,应该先考虑以下设计问题。

(2确定输出层的结点数目。对于2-类问题,一个输出结点足矣:而对于k-类问题,则需要k个输出结点。
(3选择网络拓扑结构(例如,隐藏层数和隐藏结点数,前馈还是递归网络结构)。注意,目标函数表示取决于链上的权值、隐藏结点数和隐藏层数、结点的偏置以及激活函数的类型。找出合适的拓扑结构不是件容易的事。一种方法是,开始的时候使用一个有足够多的结点和隐藏层的全连接网络,然后使用较少的结点重复该建模过程。这种方法非常耗时。另-种方法是,不重复建模过程,而是删除一些结点,然后重复模型评价过程来选择合适的模型复杂度。
(4)初始化权值和偏置。随机赋值常常是可取的。
(5)去掉有遗漏值的训练样例,或者用最合理的值来代替。
5.4.3人工神经网络的特点
(1)至少含有一个隐藏层的多层神经网络是一种普适近似(universal approximator),即可以用来近似任何目标函数。由于 ANN具有丰富的假设空间,因此对于给定的问题,选择合适的拓扑结构来防止模型的过分拟合是很重要的。
(2)ANN可以处理冗余特征,因为权值在训练过程中自动学习。冗余特征的权值非常小。(3神经网络对训练数据中的噪声非常敏感。处理噪声问题的一-种方法是使用确认集来确定模型的泛化误差,另一种方法是每次迭代把权值减少一个因子。
(4)ANN权值学习使用的梯度下降方法经常会收敛到局部极小值。避免局部极小值的方法是在权值更新公式中加上一个动量项(momentum term)。
(5训练ANN是一个很耗时的过程,特别是当隐藏结点数量很大时。然而,测试样例分类时非常快。
5.5支持向量机
支持向量机(support vector machine, SVM)已经成为一种倍受关注的分类技术。这种技术具有坚实的统计学理论基础,并在许多实际应用(如手写数字的识别、文本分类等)中展示了大有可为的实践效用。此外,SVM可以很好地应用于高维数据,避免了维灾难问题。这种方法具有一个独特的特点,它使用训练实例的一个子集来表示决策边界,该子集称作支持向量〈supportvector>。
为了解释SVM的基本思想,首先介绍最大边缘超平面(maximal margin hyperplane)的概念以及选择它的基本原理。然后,描述在线性可分的数据上怎样训练一个线性的SVM,从而明确地找到这种最大边缘超平面。最后,介绍如何将SVM方法扩展到非线性可分的数据上。
5.5.1最大边缘超平面
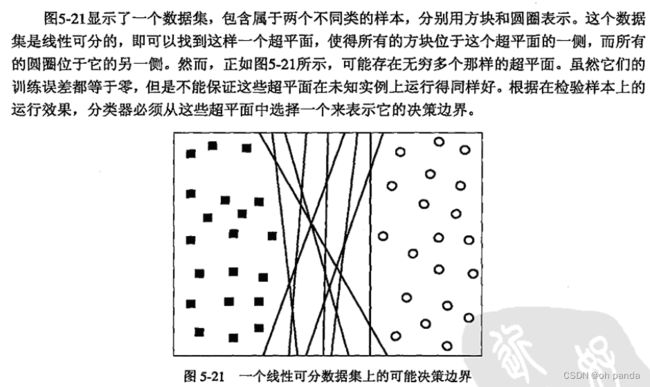

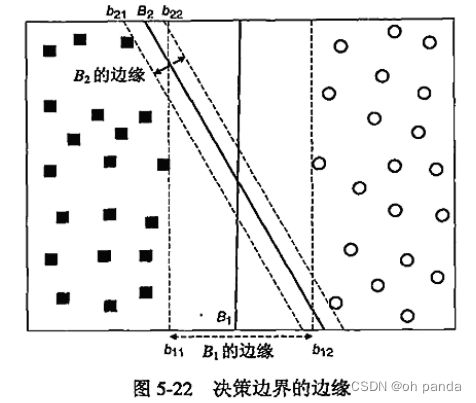

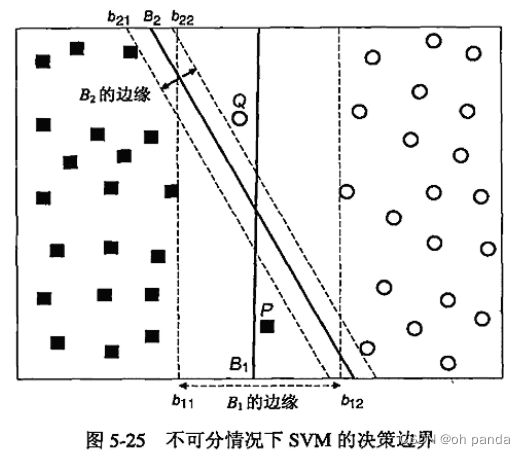
线性模型的能力与它的边缘逆相关。具有较小边缘的模型具有较高的能力,因为与具有较大边缘的模型不同,具有较小边缘的模型更灵活、能拟合更多的训练集。然而,依据SRM原理,随着能力增加,泛化误差的上界也随之提高。因此,需要设计最大化决策边界的边缘的线性分类器,以确保最坏情况下的泛化误差最小。线性SVM (linear SVM)就是这样的分类器,下一节将要详细介绍。
5.5.2线性支持向量机:可分情况
线性SVM是这样一个分类器,它寻找具有最大边缘的超平面,因此它也经常被称为最大边缘分类器
1.线性决策边界
2.线性分类器的边缘
3.学习线性SVM模型
5.5.3线性支持向量机:不可分情况
5.5.4非线性支持向量机
1.属性变换
2.学习非线性SVM模型

定义5.2 非线性 SVM非线性SVM的学习任务可以形式化地表达为以下的优化问题:
3.核技术
4.Mercer定理
对非线性SVM使用的核函数主要的要求是,必须存在一个相应的变换,使得计算一对向量的核函数等价于在变换后的空间中计算这对向量的点积。这个要求可以用Mercer定理形式化地陈述。

5.5.5支持向量机的特征
5.6组合方法
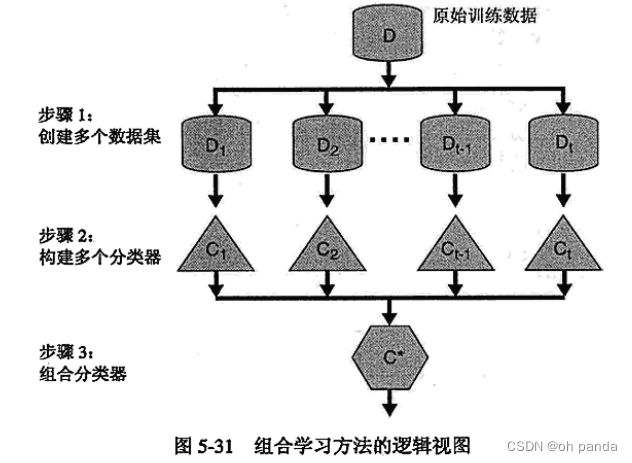
除最近邻方法外,本章迄今为止已经介绍的分类技术都是使用从训练数据得到的单个分类器来预测未知样本的类标号。本节将介绍一些技术,通过聚集多个分类器的预测来提高分类准确率。这些技术称为组合(ensemble)或分类器组合(classifier combination)方法。组合方法由训练数据构建一组基分类器(base classifier),然后通过对每个基分类器的预测进行投票来进行分类。本节将解释为什么组合方法比任意单分类器的效果好,并提供构建组合分类器的技术。
5.6.1组合方法的基本原理


组合分类器的性能优于单个分类器必须满足两个必要的条件:(1)基分类器之间应该是相互独立的;(2)基分类器应当好于随机猜测分类器。实践上,很难保证基分类器之间完全独立。尽管如此,我们看到在基分类器轻微相关的情况下,组合方法可以提高分类的准确率。
5.6.2构建组合分类器的方法
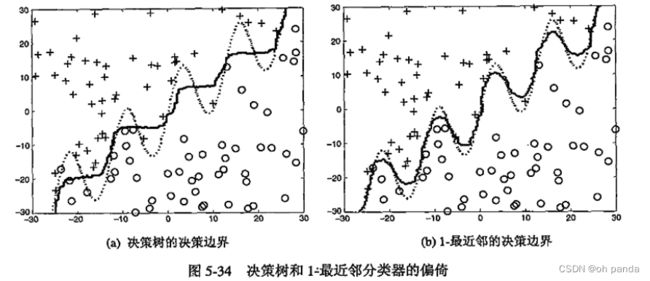
5.6.3偏倚-方差分解
5.6.4装袋


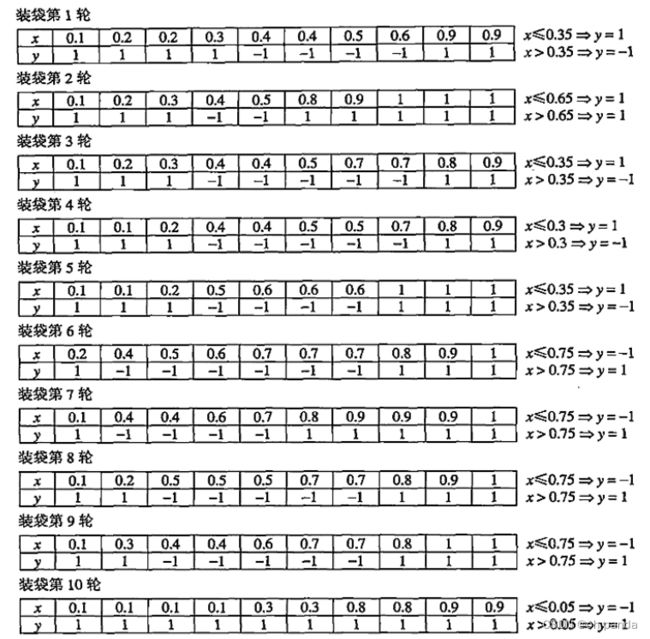

前面的例子也说明了使用组合方法的又一个优点:增强了目标函数的表达功能。即使每个基分类器都是一个决策树桩,组合的分类器也能表示一棵深度为2的决策树。
装袋通过降低基分类器方差改善了泛化误差。装袋的性能依赖于基分类器的稳定性。如果基分类器是不稳定的,装袋有助于减低训练数据的随机波动导致的误差;如果基分类器是稳定的,即对训练数据集中的徽小变化是鲁棒的,则组合分类器的误差主要是由基分类器的偏倚所引起的。在这种情况下,装袋可能不会对基分类器的性能有显著改善,装袋甚至可能降低分类器的性能,因为每个训练集的有效容量比原数据集大约小37%。
最后。由于每一个样本被选中的概率都相同,因此装袋并不侧重于训练数据集中的任何特定实例。因此,用于噪声数据,装袋不太受过分拟合的影响。
5.6.5提升
AdaBoost
5.6.6随机森林
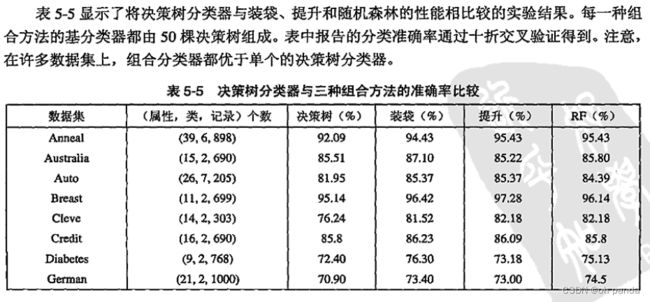
5.6.7组合方法的实验比较
5.7不平衡类问题
具有不平衡类分布的数据集在许多实际应用中都会见到。例如,一个监管产品生产线的下线产品的自动检测系统会发现,不合格产品的数量远远低于合格产品的数量。同样,在信用卡欺诈检测中,合法交易远远多于欺诈交易。在这两个例子中,属于不同类的实例数量都不成比例。不平衡程度随应用不同而不同-一一个在六西格玛原则下运行的制造厂可能会在一百万件出售给顾客的产品中发现四件不合格品,而信用卡欺诈的量级可能是百分之一。尽管它们不常出现,但是在这些应用中,稀有类的正确分类比多数类的正确分类更有价值。然而,由于类分布是不平衡的,这就给那些已有的分类算法带来了很多问题。
本节将给出一些为处理不平衡类问题而开发的方法。首先,介绍除准确率外的一些可选度量,以及一种称为ROC分析的图形化方法。然后,描述如何使用代价敏感学习和基于抽样的方法来改善稀有类的检测。
5.7.1可选度量
由于准确率度量将每个类看得同等重要,因此它可能不适合用来分析不平衡数据集。在不平衡数据集中,稀有类比多数类更有意义。对于二元分类,稀有类通常记为正类,而多数类被认为是负类。表5-6显示了汇总分类模型正确和不正确预测的实例数目的混淆矩阵。





5.7.2接受者操作特征曲线
产生ROC曲线
5.7.3代价敏感学习



有许多办法将代价信息加入分类算法中。例如,在决策树归纳过程中,代价信息可以用来:(1)选择用以分裂数据的最好的属性;(2)决定子树是否需要剪枝;(3处理训练记录的权值,使得学习算法收敛到代价最低的决策树;(4)修改每个叶结点上的决策规则。为了解释最后一种方法,令pp表示属于叶结点t的类i的训练记录所占的比例。如果下面的条件成立,一个典型的二元分类问题的决策规则将正类指派到结点t

5.7.4基于抽样的方法
5.8多类问题
纠错输出编码
第六章 关联分析:基本概念和算法
6.1问题定义



为什么使用支持度和置信度?支持度是一种重要度量,因为支持度很低的规则可能只是偶然出现。从商务角度来看,低支持度的规则多半也是无意义的,因为对顾客很少同时购买的商品进行促销可能并无益处(6.8节讨论的情况则是例外)。因此,支持度通常用来删去那些无意义的规则。此外,正如6.2.1节所示,支持度还具有一种期望的性质,可以用于关联规则的有效发现。
另一方面,置信度度量通过规则进行推理具有可靠性。对于给定的规则X→Y,置信度越高,在包含X的事务中出现的可能性就越大。置信度也可以估计Y在给定X下的条件概率。


通常,频繁项集产生所需的计算开销远大于产生规则所需的计算开销。
6.2频繁项集的产生


有几种方法可以降低产生频繁项集的计算复杂度。
1)减少候选项集的数目(M)。下一-节介绍的先验(apriori〉原理,是一种不用计算支持度值而删除某些候选项集的有效方法。
(2)减少比较次数。替代将每个候选项集与每个事务相匹配,可以使用更高级的数据结构,或者存储候选项集或者压缩数据集,来减少比较次数。
6.2.1先验原理
6.2.2Apriori算法的频繁项集产生
算法6.1Apriori算法的频繁项集产生
6.2.3候选的产生与剪枝




这种方法是完备的,因为每一个频繁t-项集都是由一个频繁(k-1)-项集和一个频繁1-项集组成的。因此,所有的频繁k-项集是这种方法所产生的候选k-项集的一部分。然而,这种方法很难避免重复地产生候选项集。例如,项集{面包,尿布,牛奶}不仅可以由合并项集{面包,尿布}和{牛奶}得到,而且还可以由合并{面包,牛奶}和{尿布}得到,或者由合并{尿布,牛奶}和{面包}得到。避免产生重复的候选项集的一种方法是确保每个频繁项集中的项以字典序存储,每个



6.2.4支持度计数
支持度计数过程确定在apriori-gen函数的候选项剪枝步骤保留下来的每个候选项集出现的频繁程度。支持度计数在算法6.1的第6步到第11步实现。支持度计数的一种方法是,将每个事务与所有的候选项集进行比较(见图6-2),并且更新包含在事务中的候选项集的支持度计数。这种方法是计算昂贵的,尤其当事务和候选项集的数目都很大时。

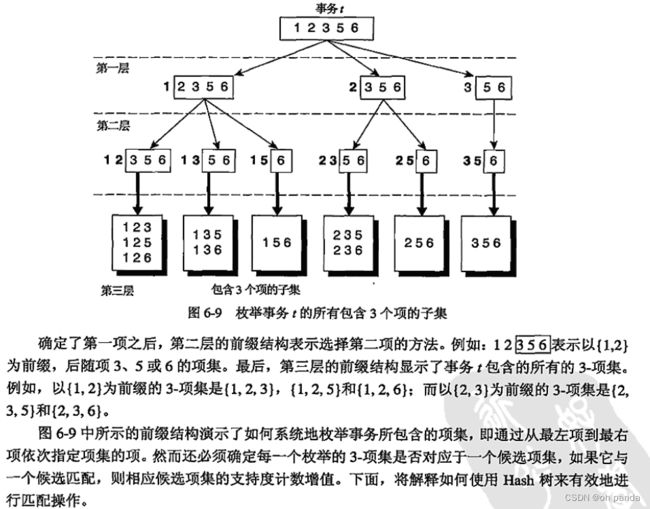
使用Hash树进行支持度计数
在Apriori算法中,候选项集划分为不同的桶,并存放在Hash树中。在支持度计数期间,包含在事务中的项集也散列到相应的桶中。这种方法不是将事务中的每个项集与所有的候选项集进行比较,而是将它与同一桶内候选项集进行匹配,如图6-10所示。


考虑一个事务t={1,2,3,5,6}。为了更新候选项集的支持度计数。必须这样遍历Hash树:所有包含属于事务t的候选3-项集的叶结点至少访问一次。注意,包含在t中的候选3-项集必须以项1,2或3开始,如图6-9中第一层前缀结构所示。这样,在Hash树的根结点,事务中的项1,2和3将分别散列。项1被散列到根结点的左子女,项2被散列到中间子女,而项3被散列到右子女。在树的下一层,事务根据图6-9中的第二层结构列出的第二项进行散列。例如,在根结点散列项1之后,散列事务的项2、3和5。项2和5散列到中间子女,而3散列到右子女,如图6-12所示。继续该过程,直至到达Hash树的叶结点。存放在被访问的叶结点中的候选项集与事务进行比较,如果候选项集是该事务的子集,则增加它的支持度计数。在这个例子中,访问了9个叶结点中的5个,15个项集中的9个与事务进行比较。
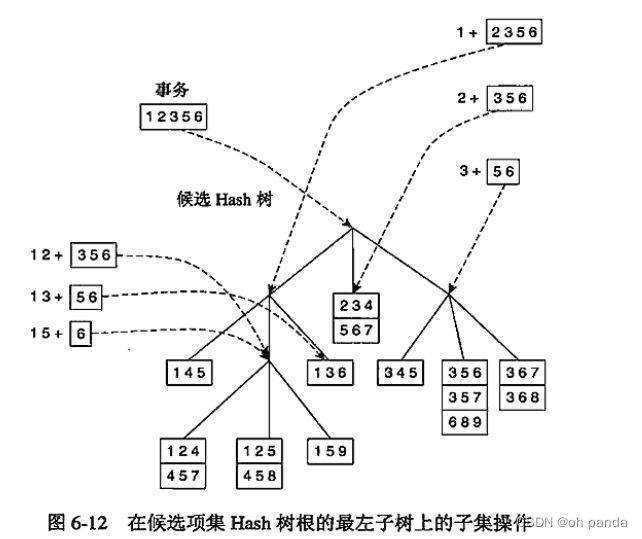
6.2.5计算复杂度
6.3规则产生
6.3.1基于置信度的剪枝
6.3.2Apriori算法中规则的产生
Apriori算法使用一种逐层方法来产生关联规则,其中每层对应于规则后件中的项数。初始,提取规则后件只含一个项的所有高置信度规则,然后,使用这些规则来产生新的候选规则。例如,

6.4频繁项集的紧凑表示
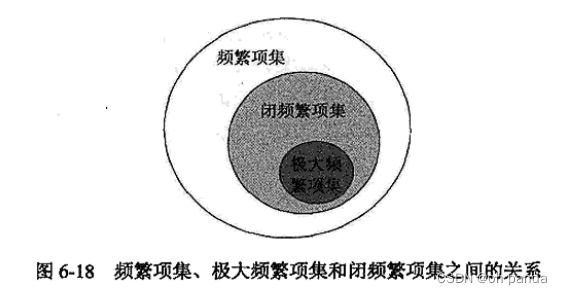
实践中,由事务数据集产生的频繁项集的数量可能非常大。因此,从中识别出可以推导出其他所有的频繁项集的、较小的、具有代表性的项集是有用的。本节将介绍两种具有代表性的项集:极大频繁项集和闭频繁项集。
6.4.1极大频繁项集
定义6.3极大频繁项集(maximal frequent itemset)极大频繁项集是这样的频繁项集,它的直接超集都不是频繁的。

6.4.2闭频繁项集
定义6.4︰闭项集(closed itemset)项集X是闭的,如果它的直接超集都不具有和它相同的支持度计数。

定义6.5闭频繁项集(closed frequent itemset)一个项集是闭频繁项集,如果它是闭的,并且它的支持度大于或等于最小支持度阙值。




6.5产生频繁项集的其他方法
6.6FP增长算法
使用一种称作FP树的紧凑数据结构组织数据,并直接从该结构中提取频繁项集。
6.6.1 FP树表示法
6.6.2FP增长算法的频繁项集产生
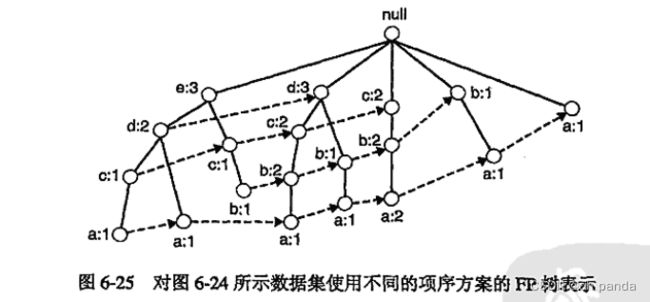
FP增长(FP-growth)是一种以自底向上方式探索树,由P树产生频繁项集的算法。给定图6-24所示的树,算法首先查找以e结尾的频繁项集,接下来依次是d, c,b,最后是a。这种用于发现以某一个特定项结尾的频繁项集的自底向上策略等价于6.5节介绍的基于后缀的方法。由于每一个事务都映射到F树中的一条路径,因而通过仅考察包含特定结点(例如e)的路径,就可以发现以·e结尾的频繁项集。使用与结点e相关联的指针,可以快速访问这些路径。图6-26a显示了所提取的路径。稍后详细解释如何处理这些路径,以得到频繁项集。





6.7关联模式的评估
1.其他客观兴趣度度量
2.客观度量的一致性
3.客观度量的性质
6.7.2多个二元变量的度量
6.7.3辛普森悖论
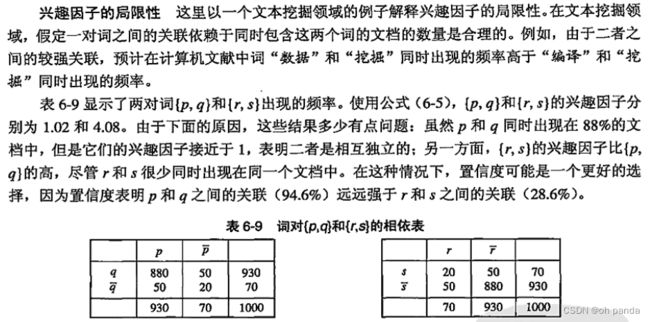
6.8倾斜支持度分布的影响
第七章 关联分析:高级概念
本章将这种表示扩展到具有对称二元属性、分类属性和连续属性的数据集。这种表示还将进一步扩充到包含诸如序列和图形的更复杂的实体。尽管关联分析算法的总体结构保持不变,但是算法的某些方面必须加以修改,以便处理非传统的实体。
7.1处理分类属性
7.2处理连续属性
7.2.1基于离散化的方法
7.2.2基于统计学的方法
7.2.3非离散化方法
7.3处理概念分层
概念分层是什么:定义在一个特定的域中的各种实体或概念的多层组织。
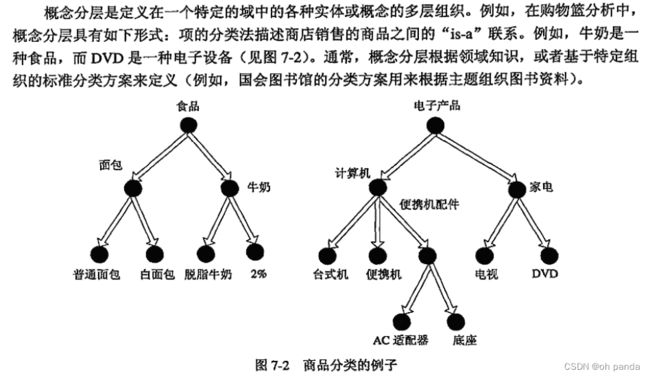
7.4序列模式
7.4.2序列模式发现
序列s的支持度是包含s的所有数据序列所占的比例。如果序列s的支持度大于或等于用户指定的阙值 minsup,则称s是一个序列模式(或频繁序列)。
定义7.1序列模式发现―给定序列数据集D和用户指定的最小支持度阙值minsup,序列模式发现的任务是找出支持度大于或等于minsup 的所有序列。


算法7.1序列模式发现的类Apriori算法
7.4.3时限约束
7.5子图模式
7.5.1图与子图
7.5.2频繁子图挖掘
7.5.3类Apriori方法
7.5.4候选产生
7.5.5候选剪枝
产生候选k-子图后,需要剪去(k-1)-子图非频繁的候选。候选剪枝可以通过如下步骤实现:



7.6非频繁模式
定义7.7非频繁模式非频繁模式是一个项集或规则,其支持度小于阈值minsup。
7.6.1负模式
7.6.2负相关模式
7.6.3非频繁模式、负模式和负相关模式比较
7.6.4挖掘有趣的非频繁模式的技术
7.6.5基于挖掘负模式的技术
7.6.6基于支持度期望的技术
算法7.2挖掘间接关联的算法
第八章 聚类分析:基本概念和算法
8.1概述
8.1.1什么是聚类分析
8.1.2不同的聚类类型
8.1.3 不同的簇类型
8.2K均值
8.2.1基本K均值算法
算法8.1基本K均值算法
8.2.2 K均值:附加的问题
8.2.3二分K均值
二分K均值算法是基本K均值算法的直接扩充,它基于一种简单想法:为了得到K个簇,将所有点的集合分裂成两个簇,从这些簇中选取一个继续分裂,如此下去,直到产生K个簇。
算法8.2二分K均值算法
8.2.4 K均值和不同的簇类型
8.2.5优点与缺点
K均值简单并且可以用于各种数据类型。它也相当有效,尽管常常多次运行。K均值的某些变种(包括二分K均值〉甚至更有效,并且不太受初始化问题的影响。
然而,K均值并不适合所有的数据类型。它不能处理非球形簇、不同尺寸和不同密度的簇,尽管指定足够大的簇个数时它通常可以发现纯子簇。对包含离群点的数据进行聚类时,K均值也有问题。在这种情况下,离群点检测和删除大有帮助。最后,K均值仅限于具有中心(质心)概念的数据。一种相关的K中心点聚类技术没有这种限制,但开销更大。
8.2.6 K均值作为优化问题
8.3凝聚层次聚类
8.3.1基本凝聚层次聚类算法
8.3.2特殊技术
8.3.3簇邻近度的Lance-Williams 公式
8.3.5优点与缺点
具体的凝聚层次聚类算法的优缺点上面已经讨论过。通常,使用这类算法是因为基本应用(如创建一种分类法)需要层次结构。此外,有些研究表明,这些算法能够产生较高质量的聚类。然而,就计算量和存储需求而言,凝聚层次聚类算法是昂贵的。所有合并都是最终的,对于噪声、高维数据(如文档数据),这也可能造成问题。先使用其他技术(如K均值〉进行部分聚类,这两个问题都可以在某种程度上加以解决。
8.4 DBSCAN
基于密度的聚类寻找被低密度区域分离的高密度区域。DBSCAN是一种简单、有效的基于密度的聚类算法,它解释了基于密度的聚类方法的许多重要概念。本节中,在考虑密度的主要概念之后,我们仅关注DBSCAN。其他基于密度的聚类算法将在下一章介绍。
8.4.1传统的密度:基于中心的方法
8.4.2DBSCAN算法
8.4.3优点与缺点
因为DBSCAN使用簇的基于密度的定义,因此它是相对抗噪声的,并且能够处理任意形状和大小的簇。这样,DBSCAN可以发现使用K均值不能发现的许多簇,如图8-22中的那些簇。然而,如前所述,当簇的密度变化太大时,DBSCAN 就会有麻烦。对于高维数据,它也有问题,因为对于这样的数据,密度定义更困难。处理这些问题的一种可行的方法在94.8节给出。最后,当近邻计算需要计算所有的点对邻近度时(对于高维数据,常常如此),DBSCAN 的开销可能是很大的。
8.5簇评估
对于监督分类,结果分类模型的评估是分类模型开发过程中必不可少的部分:并且存在广泛接受的评估度量和过程,如准确率和交叉确认。然而,由于簇的特性,簇评估技术未很好开发,或者说不是聚类分析普遍使用的。尽管如此,簇评估,或者使用更传统的称呼,簇确认(cluster validation),是重要的。
簇评估应当是聚类分析的一部分。它的主要目的是,几乎每种聚类算法都会在数据集中发现簇,即便该数据集根本没有自然的簇结构。
8.5.1概述
8.5.2非监督簇评估:使用凝聚度和分离度
对于划分的聚类方案,簇有效性的许多内部度量都基于凝聚度和分离度概念。

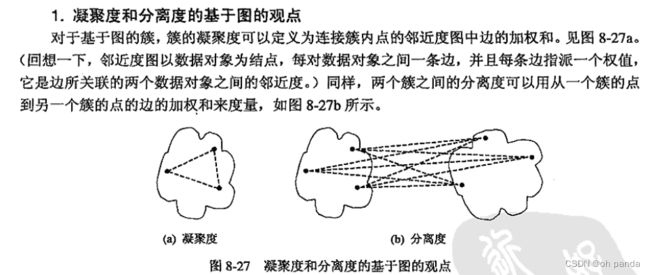


注意,簇的有效性的任何非监督度量都可以作为聚类算法的目标函数使用,反之亦然。



![]()
![]()

8.5.3非监督簇评估:使用邻近度矩阵
8.5.4层次聚类的非监督评估
8.5.5确定正确的簇个数
8.5.6聚类趋势
8.5.7簇有效性的监督度量
8.5.8评估簇有效性度量的显著性
第九章 聚类分析:其他问题与算法
9.1数据、簇和聚类算法的特性
9.1.1例子:比较K均值和DBSCAN
9.1.2数据特性
9.1.3簇特性
9.1.4聚类算法的一般特性
9.2基于原型的聚类
9.2.1模糊聚类
算法9.1基本模糊c均值算法
9.2.2使用混合模型的聚类
算法9.2EM算法
4.使用EM算法的混合模型聚类的优点和局限性
9.2.3自组织映射
1.SOM算法
算法9.3基本SOM算法
2.应用
9.3基于密度的聚类
9.3.1基于网格的聚类
网格是-一-种组织数据集的有效方法,至少在低维空间中如此。其基本思想是,将每个属性的可能值分割成许多相邻的区间,创建网格单元的集合(对于这里和本节其余部分的讨论,我们假·定属性值是序数的、区间的或连续的)。每个对象落入一个网格单元,网格单元对应的属性区间包含该对象的值。扫描一遍数据就可以把对象指派到网格单元中,并且还可以同时收集关于每个单元的信息,如单元中的点数。
算法9.4基本的基于网格的聚类算法
3.由稠密网格单元形成簇
4、优点与局限性
9.3.2子空间聚类
迄今为止,所考虑的聚类技术都是使用所有的属性来发现簇。然而,如果仅考虑特征子集(即数据的子空间),则我们发现的簇可能因子空间不同而很不相同。有两个理由可以推断子空间的簇是有意义的。第一,数据关于少量属性的集合可能可以聚类,而关于其余属性是随机分布的。第二,在某些情况下,在不同的维集合中存在不同的簇。考虑记录不同时间、不同商品销售情况的数据集(时间是维,而商品是对象),某些商品对于特定的月份集(如夏季)可能表现出类似行为,但是不同的簇可能被不同的月份(维)刻画。
1.CLIQUE
算法9.5CLIQUE算法
2.CLIQUE的优点与局限性
CLIQUE的最有用的特征是,它提供了一种搜索子空间发现簇的有效技术。由于这种方法基于源于关联分析的著名的先验原理,它的性质能够被很好地理解。另一个有用特征是 CLIQUE用一小组不等式概括构成一个簇的单元列表的能力。
CLIQUE的许多局限性与前面讨论过的其他基于网格的密度方法相同。其他局限性类似于Apriori算法。具体地说,正如频繁项集可以共享项一样,CLIQUE发现的簇也可以共享对象。允许簇重叠可能大幅度增加簇的个数,并使得解释更加困难。另一个问题是Apriori(和 CLIQUE)潜在地具有指数复杂度。例如,如果在较低的k值产生过多的稠密单元,则CLIQUE将遇到困难。提高密度阈值g可以减缓该问题。CLIQUE的另一个潜在的局限性在本章习题20中考察。
9.3.3 DENCLUE:基于密度聚类的一种基于核的方案
算法9.6 DENCLUE 算法
1、核密度估计
DENCLUE基于一个发展完善的统计学和模式识别领域,称作核密度估计(kernel densityestimation)。这些技术(以及其他许多统计技术)的目标是用函数描述数据的分布。对于核密度估计,每个点对总密度函数的贡献用一个影响(influence)或核函数(kernel function)表示。总密度函数仅仅是与每个点相关联的影响函数之和。
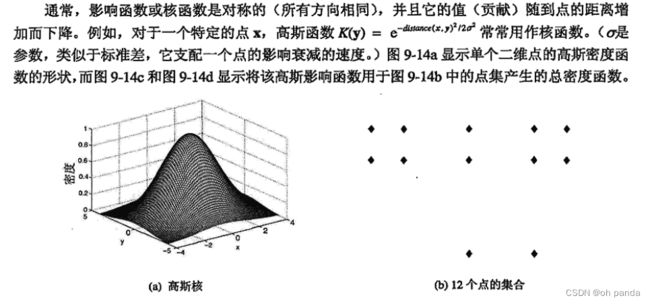
2.实现问题
为了降低时间复杂度,DENCLUE使用一种基于网格的实现来有效地定义近邻,并借此限制定义点的密度所需要考虑的点的数量。首先,预处理步创建网格单元集。仅创建被占据的单元,并且这些单元及其相关信息可以通过搜索树有效地访问。然后计算点的密度。并找出其最近的密度吸引点。DENCLUE只考虑近邻中的点,即相同单元或者与该点所在单元相连接的单元中的点。尽管这种方法牺牲了一些密度估计的精度,但是计算复杂度大大降低。
3.DENCLUE的优点与局限性
9.4基于图的聚类
9.4.1稀疏化
9.4.2最小生成树聚类
算法9.7MST分裂层次聚类算法
9.4.3OPOSSUM:使用METIS的稀疏相似度最优划分
OPOSSUM(Optimal Partitioning of Sparse Similarities Using METTS)是一种专门为诸如文档或购物篮数据等稀疏、高维数据设计的聚类技术。与MST一样,它基于邻近度图的稀疏化进行聚类。然而,OPOSSUM使用METTIS 算法,该算法是专门为划分稀疏图设计的。OPOSSUM的步骤在算法9.8中给出。
算法9.8 OPoSSUM 聚类算法
9.4.4Chameleon:使用动态建模的层次聚类
凝聚层次聚类技术通过合并两个最相似的簇来聚类,其中簇的相似性定义依赖于具体的算法。有些凝聚聚类算法,如组平均,将其相似性概念建立在两个簇之间的连接强度上(例如,两个簇中点的逐对相似性),而其他技术,如单链方法,使用簇的接近性(例如,不同簇中点的最小距离)来度量簇的相似性。尽管有两种基本方法,但是仅使用其中一种方法可能导致错误的簇合并。


2.Chameleon算法
Chameleon算法由三个关键步骤组成:稀疏化、图划分和层次聚类。
算法9.9Chameleon算法
4.优点与局限性
Chameleon 能够有效地聚类空间数据,即便存在噪声和离群点,并且簇具有不同的形状、大小和密度。Chameleon假定由稀疏化和图划分过程产生的对象组群是子簇,即一个划分中的大部分点属于同一个真正的簇。
如果不是,则凝聚层次聚类将混合这些错误,因为它绝对不可能再将已经错误地放到一起的对象分开(见8.3.4节的讨论)。这样,当划分过程未产生子簇时, Chameleon就有问题:对于高维数据,常常出现这种情况。
9.4.5共享最近邻相似度
一般地说,如果直接相似度低,则对于聚类,特别是凝聚层次聚类(最近的点放在一起,并且不能再分开),相似度将成为不可靠的指导。尽管如此,一个对象的大多数最近邻通常仍然属于同一个类;这一事实可以用来定义更适合聚类的邻近性度量。


算法9.10计算共享最近邻相似度
9.4.6Jarvis-Patrick聚类算法
算法9.11Jarvis-Patrick聚类算法
9.4.7 SNN密度
9.4.8基于SNN密度的聚类
算法9.12基于SNN密度的聚类算法
9.5可伸缩的聚类算法
如果运行时间长得不可接受,或者需要的存储量太大,即使最好的聚类算法也没有多大价值。本节考察着重强调可扩展到超大型数据集的聚类技术,这种超大型数据集正变得越来越常见。首先,我们讨论可伸缩的某些一般策略,包括降低邻近度计算数量的方法、数据抽样、数据划分和对数据的汇总表示聚类。然后,我们讨论两个具体的可伸缩聚类算法:CURE和BIRCH。
9.5.1 可伸缩:一般问题和方法
9.5.2BIRCH
算法9.13BIRCH
9.5.3 CURE
算法9.14 CURE
9.6使用哪种聚类算法




第10章 异常检测
异常检测的目标是发现与大部分其他对象不同的对象。
通常,异常对象被称作离群点(outlier),因为在数据的散布图中,它们远离其他数据点。异常检测也称偏差检测(deviationdetection),因为异常对象的属性值明显偏离期望的或常见的属性值。
异常检测也称例外挖掘(exception mining),因为异常在某种意义上是例外的。

异常检测(和消除)通常是数据预处理的一部分。
10.1预备知识
10.1.1异常的成因
一些常见的异常成因:数据来源于不同的类,自然变异,以及数据测量或收集误差。

10.1.2异常检测方法
10.1.3类标号的使用
10.1.4问题
10.2统计方法
10.2.1检测一元正态分布中的离群点
10.2.2多元正态分布的离群点
10.2.3异常检测的混合模型方法
本节提供一种使用混合模型方法的异常检测技术。聚类(见9.2.2节)时,混合模型方法假定数据来自混合概率分布,并且每个簇可以用这些分布之一识别。同样,对于异常检测,数据用两个分布的混合模型建模,一个分布为普通数据,而另一个为离群点。