使用QIS(Quantum Image Sensor)图像重建总结(2)
4 使用QIS来获得彩图
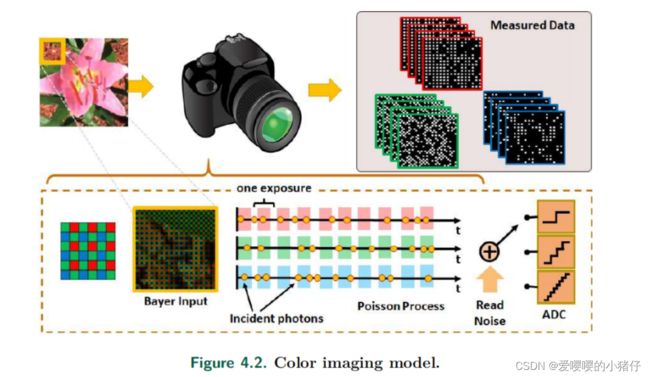
彩色图像通常通过在图像传感器前面放一个彩色滤波器阵列(color filter array, CFA)获得,比如贝叶斯模式CFA,它的每个像素只有一个颜色通道。所捕获的图像将是一个不同颜色的马赛克,如图4.1所示。将这个单通道的马赛克图像转换成三通道的RGB图像称为去马赛克。去马赛克是一项困难的任务,因为我们本质上在做超像素处理,即将每像素一颜色通道转化为每像素三颜色通道。我们需要处理颜色通道的对齐,这需要细致的处理。光子有效的场景下,将进一步增加其难度,因为需要同时处理去马赛克和严重的噪声。
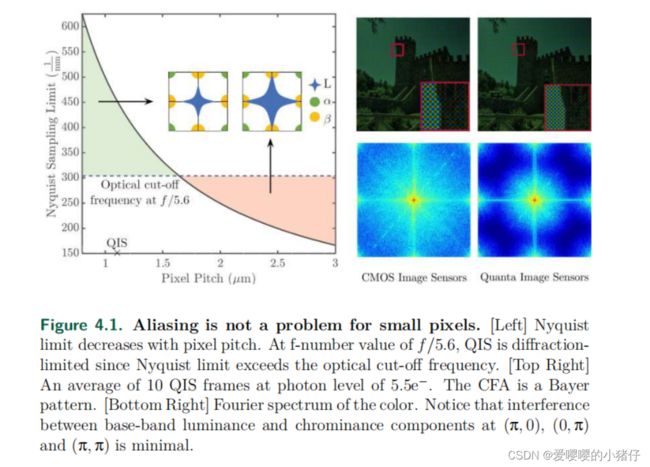
传统的CIS去噪算法通常强调缓解混叠(又名Moire伪影),例如,使用先进的边缘感知除噪方法或使用后处理模块去除除噪伪影。然而,当像素很小时,混叠并不是一个大问题(如图4.1所示),因为衍射极限,可以认为是衍射引入的轻微模糊。由于衍射,混叠不再占主导地位。但是,请注意,由于衍射,图像会被模糊,需要进一步处理才能去模糊。我们并不担心这章中的这种模糊。如果我们忽略模糊,我们可以使用一个简单的方法来去解噪,可能是一些传统的方法,如线性解调和去噪,来重建颜色。
为了详细说明混叠问题,我们在图4.1中展示了三个插图。在图4.1(a)中,我们绘制了彩色滤光片阵列的奈奎斯特采样限制作为像素间距的函数,并说明了与采样限制相关的双色光谱。奈奎斯特极限定义了防止混叠所需的最低空间采样频率。当像素变得很小时,我们有效地对场景进行过采样,增加了奈奎斯特极限。以f/5.6光学系统为例,我们所能负担得起的最大像素间距为1.6µm,它安全地高于当前CIS-QIS的1.1µm间距。可以通过图4.1(b)和4.1©中的合成数据做进一步地证明,这里展示了CFA数据和它对应的光谱。我们可以发现,由于更小的像素尺寸,QIS可以提供更好的光谱。
相关工作
传统去马赛克算法:传统的去马赛克算法通常都是针对拥有良好照明条件的CIS设计的。在低光照条件下,由于噪声严重,去马赛克算法必须拥有好的去噪能力。同时需要注意到,去噪和去马赛克的顺序是很重要的。如果先去马赛克,则插值会破坏噪声的空间独立性,这回使得去噪过程变得复杂。如果先去噪,然后大部分的图像先验不能被使用,因为马赛克图像没有自然的图像统计数据。因而同时进行去马赛克处理和去噪处理是一个更好的选择。然而,大部分的同时去马赛克和去噪方法都是迭代的。
基于深度学习的去马赛克方法:现有的SOTA去马赛克方法基本上都是基于深度学习方法的。这个想法是修改一个通用的深度神经网络,通过添加一个从空间到深度的层,将原始的拜耳图像转化为4个具有四分之一分辨率的拜耳通道。神经网络处理这些下采样的通道,然后使用深度到空间层对其进行上采样,得到满分辨率的彩色图像。
在本章中,我们提出两种方法:一种经典方法,一种深度学习去马赛方法。这两种方法都考虑了噪声和颜色成像背后的物理原理。
基于 Plug-and-play ADMM的图像重建
修改后的图像模型
我们首先介绍了我们在第三章中介绍的成像模型的一些小的变化。回想一下,在没有暗噪声和其他不均匀性的情况下,如果我们假设场景没有随着积分时间的变化而变化,我们可以把照相机的成像模型写成:

这里 β ∈ R N \beta\in\mathbb{R}^N β∈RN是我们想要估计的真实强度( N N N是总的像素数量), α \alpha α和积分时间成正比,决定了平均光子水平, σ r e a d \sigma_{read} σread是读出噪声。我们假设第三章中的ADC偏置 O O O为0。
对于彩色成像,我们认为,对于每一个像素, β \beta β包含了不同的颜色通道。然而,这在这里并不是一个方便的符号,因为我们希望恢复每个像素的所有三个通道。所以我们在成像模型中做了一个小的调整。

其中 θ ∈ R 3 N \theta\in \mathbb{R}^{3N} θ∈R3N包含了三个通道(R,G,B)。 S ∈ R M × 3 M S\in \mathbb{R}^{M\times 3M} S∈RM×3M是一个带有1和0的fat matrix,它根据所使用的彩色滤波器阵列(CFA)来决定每个像素对应的颜色通道。
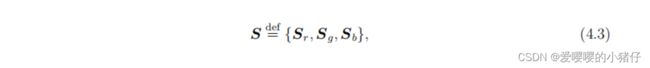
其中, S r , S g \textbf{S}_r,\textbf{S}_g Sr,Sg和 S b \textbf{S}_b Sb都是对角线为1和0的对角矩阵,并且有 S r + S g + S b = I \textbf{S}_r+\textbf{S}_g+\textbf{S}_b=\mathbb{I} Sr+Sg+Sb=I。记住,在这种情况下,我们想要恢复 θ \mathbb{\theta} θ。
在这一章中,我们会处理单位的ADC以及多位的ADC。对于多位的成像,我们假设转化增益 G = 1 G=1 G=1,对于单位ADC,我们使用任意的整数作为转化增益 G G G。
4.2.2 联合去噪和去马赛克
图像重建的任务是从测量值 Y = { Y 1 , … Y T } \mathcal{Y} = \{\textbf{Y} _1,…\textbf{Y}_T \} Y={Y1,…YT}中恢复彩色场景 θ θ θ,其中 T T T是捕获的帧数。在灰度设置下,我们可以将问题表示为最大似然问题,并使用凸优化工具来求解它。我们也可以使用基于学习的方法。我们在这里提出的方法是基于Chan等人的变换-去噪方法。变换-去噪是一种基于物理的方法,对不同的传感器配置具有鲁棒性。例如,在基于学习的方法中,如果我们改变帧数和,我们需要训练一个不同的模型或神经网络。
4.2.3 重建流程
重建算法的流程如图4.3所示。给定测量值 Y = { Y 1 , … Y T } \mathcal{Y} = \{\textbf{Y} _1,…\textbf{Y}_T \} Y={Y1,…YT},我们首先计算出均值来生成单张图像 Z \textbf{Z} Z:
Z = 1 T ∑ t = 1 T Y t (4.4) \textbf{Z}=\frac{1}{T}\sum^T_{t=1}\textbf{Y} _t\tag{4.4} Z=T1t=1∑TYt(4.4)
如果我们愿意,这一步可以集成到相机的硬件中,这样相机的输出将是多帧的平均值。
如果我们假设除了时间平均之外没有对bit的处理,那么如式(3.69)所示,使用均值不变性,我们可以将估计量 β ^ \hat{\beta} β^写为:
β ^ = μ − 1 ( Z ) \hat{\beta}=\mu^{-1}(Z) β^=μ−1(Z)
其中, μ ( β ) \mu(\beta) μ(β)是将基础参数 β β β映射到变量 Z Z Z的对应均值的均值函数( μ ( β ) = E ( Z ) \mu(\beta)=E(Z) μ(β)=E(Z))。

方差稳定变换
现在,我们想要处理数据而不是平均帧。然而,无论是单位(bit)还是多位模式,对二项分布或者泊松分布进行统计都不容易,因为其方差随着均值而变化。这样就无法使用基于高斯分布的现有算法。为了使用这些基于高斯噪声开发的算法(这些算法假设整个图像的噪声强度是均匀的),我们需要用一种技术将整个图像上的噪声稳定到相同强度。这种技术称为方差稳定变换(variance stabilizing transform, VST)。图4.4展示了VST在泊松数据上的效果。

对于单位的VST,由于随机变量是一个二项随机变量,使用Ancombe变换得:
T s i n g l e − b i t ( z ) = d e f T + 1 2 s i n − 1 z + 3 8 T + 3 4 (4.6) \mathcal{T}_{single-bit}(\textbf{z})\overset{\mathrm{def}}{=}\sqrt{T+\frac{1}{2}}sin^{-1}\sqrt{\frac{\textbf{z}+\frac{3}{8}}{T+\frac{3}{4}}}\tag{4.6} Tsingle−bit(z)=defT+21sin−1T+43z+83(4.6)
对于多位的,我们采用延迟路径,并且假设像素在多位下不饱和,并且使用简单泊松随机分布对应的VST:
T m u l t i − b i t ( z ) = d e f z + 3 8 (4.7) \mathcal{T}_{multi-bit}(\textbf{z})\overset{\mathrm{def}}{=}\sqrt{\textbf{z}+\frac{3}{8}}\tag{4.7} Tmulti−bit(z)=defz+83(4.7)
,
如果我们对帧 z \textbf{z} z采用适当的 V S T τ ( ⋅ ) VST \tau(\cdot) VSTτ(⋅),噪声就会稳定下来,我们可以使用任意的高斯方法进行去马赛克和去噪。这个问题可以表述为:

其中, v ∈ R 3 \textbf{v}\in\mathbb{R}^3 v∈R3使我们打算恢复的RGB图像, g g g是控制 v \textbf{v} v平滑度的正则函数。式(4.8)是基于高斯噪声的标准去噪和去马赛克问题。
联合重建和去马赛克
式(4.8)中的优化问题是一个具有正则化函数 g g g的标准最小二乘问题。因此,只要 g g g是凸的,就可以使用大多数凸优化算法。这一部分使用了ADMM(alternating direction method of multiplier)的变式,通过用现成的图像去噪器替代 g g g,这种方法叫做PnP(Plug-and-play) ADMM。
对于式(4.8)中的问题,PnP ADMM迭代更新下面两步:

然后,使用 u ( k + 1 ) = u ( k ) − ( x ( k + 1 ) − v ( k + 1 ) ) u^{(k + 1)}= u^{(k)}-(x^{(k + 1)}-v^{(k + 1)}) u(k+1)=u(k)−(x(k+1)−v(k+1))更新拉格朗日乘数。(详细可以参考论文:Plug-and-play ADMM for image restoration: Fixed-point convergence and applications) ρ \rho ρ是控制收敛性的内部参数。 D D D运算符是一个现成的图像去噪器,例如块匹配和3D滤波(BM3D)或深度神经网络去噪器。下标ρ/λ表示去噪强度,即假定的“噪声方差”。由于 S T S S^TS STS是对角矩阵,因此求逆是逐点进行的。
非迭代算法
QIS的1.1µm像素间距可能导致空间分辨率与传统CMOS传感器相同甚至更高。在某些应用中,我们可以在颜色重建效率和分辨率之间进行权衡。例如,我们可以使用四个jot代替一个像素,如图4.5所示。

使用四个jot代替一个像素可以让我们绕过迭代的ADMM步骤,因为不再有缺失像素问题。在这种情况下,矩阵 S ∈ R M × 3 M S∈\mathbb{R}^{M×3M} S∈RM×3M将变为 S = d i a g { 1 4 I , 1 2 I , 1 4 I } ∈ R 3 M × 3 M S=diag\{\frac{1}{4}I,\frac{1}{2}I,\frac{1}{4}I\}∈\mathbb{R}^{3M×3M} S=diag{41I,21I,41I}∈R3M×3M,因此方程(4.8)简化为具有三个通道不同噪声水平的去噪问题。特别地,绿色通道的方差是红色和蓝色的一半。对于实现,我们可以修改去噪器,例如BM3D以适应不同的噪声方差。由于不再有ADMM迭代,算法显著加快。虽然我们使用BM3D来演示结果,但任何用于CIS基础相机的现成去噪器都可以用于去噪四个jot到一个像素的方法。我们还想强调,Anscombe变换和变换M都可以作为查找表来实现。因此,这种方法可以像CIS基础相机中当前使用的去噪器一样快。
4.2.4 实验结果
基于学习的去马赛克方法
我们将探讨基于深度学习的去马赛克方法,同样我们会考虑彩色图像的物理性质。
4.3.1 创新
1、频率选择:所提出的去马赛克算法是基于经典的滤色器阵列理论。我们开发了一个颜色处理模块,通过选择彩色滤色器阵列的已知载波频率来解调颜色通道。现有的基于深度学习的解决方案使用通用的卷积神经网络,在很大程度上不使用滤色器阵列的物理特性。
2、引导重建:所提出的方法运用了物理常识:luma通道拥有比色谱通道更好的SNR。因此,luma通道保存的信号细节可以被用来指引色谱通道的滤波。现有的卷积神经网络没有探索数据的这些特征。
4.3.2 频率选择去马赛克网络
本方法使用了经典的频率选择方法,并且进行了修改。在这一部分,我们首先提供关于频率选择的背景。随后,介绍了对学习去马赛克低通滤波器和使用亮度(luma)通道引导色度通道的滤波的修改。我们还介绍了损失函数和训练过程。
频率选择
考虑一个彩色图像 y r g b ∈ R H × W × 3 y_{rgb}\in R^{H\times W\times 3} yrgb∈RH×W×3,我们将像素 ( m , n ) (m,n) (m,n)处的红色、绿色以及蓝色通道中的归一化强度表示为:

这里 m = 0 , . . . , H − 1 , n = 0 , . . . , W − 1 m=0,...,H-1,n=0,...,W-1 m=0,...,H−1,n=0,...,W−1。彩色图像 y r g b ∈ R H × W × 3 y_{rgb}\in R^{H\times W\times 3} yrgb∈RH×W×3通过CFA下采样后得到了马赛克图像 y C F A ∈ R H × W y_{CFA}\in R^{H\times W} yCFA∈RH×W。假设CFA遵循标准的拜耳模式,那么可以证明马赛克处图像的像素 ( m , n ) (m,n) (m,n)采用了这种形式(可以参考论文:Frequency-domain methods for demosaicking of bayer-sampled color images和Linear demosaicing inspired by the human visual system):

这里 y L , y α y_L,y_{\alpha} yL,yα和 y β y_{\beta} yβ定义为潜在的RGB颜色像素的线性变换:

注意到式(4.12)是一个前项模型。也就是说,给定亮度和色度成分 ( y L , y α , y β ) (y_L,y_\alpha,y_\beta) (yL,yα,yβ),我们可以决定 y C F A y_{CFA} yCFA。它的逆问题,也就是去马赛克问题,也就是从 y C F A y_{CFA} yCFA中求得 ( y L , y α , y β ) (y_L,y_\alpha,y_\beta) (yL,yα,yβ)。
频率选择的出发点是查看 y C F A y_{CFA} yCFA的傅里叶谱。如果我们取 y C F A y_{CFA} yCFA的二维离散傅里叶变换,我们可以证明 y C F A y_{CFA} yCFA的频率表示为:

其中, μ \mu μ和 v v v表示2D角频率, ( ⋅ ~ ) (\tilde{\cdot}) (⋅~)表示傅里叶变换。式(4.14)表明马赛克图像的光谱 y C F A y_{CFA} yCFA包含了一个亮度通道 y ~ L \tilde{y}_L y~L,两个 α \alpha α色度通道 y ~ α 1 \tilde{y}_{\alpha_1} y~α1和 y ~ α 2 \tilde{y}_{\alpha_2} y~α2以及一个 β \beta β色度通道 y ~ β \tilde{y}_{\beta} y~β。图4.10展示了频率分析的思想。给定一张彩图,我们可以检查由彩色滤波器阵列生成的图像。在频域内,亮度通道占据了光谱的中心,而色度通道则位于光谱的两侧。

式(4.14)中的傅里叶谱说明CFA可以有效地对颜色通道进行调制。因此,一个去马赛克的方法就是对 y C F A y_{CFA} yCFA进行解调,从而还原 ( y L , y α , y β ) (y_L,y_\alpha,y_\beta) (yL,yα,yβ)。解调在这里是可行的,因为我们从二维域采样定理的基本原理中知道CFA和它的载波频率。如果记 y α 1 , y α 2 y_{α_1},y_{α_2} yα1,yα2和 y β y_β yβ的载波频率分别为 ω α 1 , ω α 2 ω_{α_1},ω_{α_2} ωα1,ωα2和 ω β ω_β ωβ,则将载波定义为(以 α 1 α_1 α1为例):
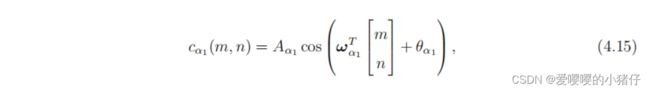
其中, A α 1 A_{\alpha_1} Aα1和 θ α 1 \theta_{\alpha_1} θα1是载波的振幅和相位偏移量。为了解调颜色,我们将 y C F A ( m , n ) y_{CFA}(m,n) yCFA(m,n)与载波 c α 1 ( m , n ) c_{\alpha_1}(m,n) cα1(m,n)相乘,然后和预先定义的低通滤波器 g ( m , n ) g(m,n) g(m,n)进行卷积:

y α 2 y_{\alpha_2} yα2和 y β y_\beta yβ的计算类似。为了简单起见,我们通过平均采样来结合这两个 α \alpha α通道:

通过从输入的CFA图像中减去重新调制的 y α 1 , y α 2 y_{α_1},y_{α_2} yα1,yα2和 y β y_β yβ分量来恢复基带亮度分量:

整个解调的过程如图4.11所示。输入的CFA图像首先和载波相乘。在傅里叶频域(底部的红色曲线),光谱会随着载波频率的变化而转移。由于我们知道CFA,载波的频率是确定的。然后我们将信号通过一个低通滤波器。在这之后,我们再次将信号和载波进行相乘以还原光谱。
为了可以自定义地进行频率选择,我们是低通滤波器可训练。具体来说,我们使用三层 7 × 7 7\times 7 7×7的卷积核来重建垂直、水平和对角线色度通道。再训练过程中,通过对滤波器相关系数进行 l 1 l_1 l1正则化来使其一致。这种滤波器估计更加灵活,因为它在端到端训练中联合执行了滤波器估计和亮度、色度去噪。

引导滤波
频率选择阶段的输出由亮度信号 y L y_L yL和两个色度信号 y α y_α yα和 y β y_β yβ组成。所有的信号都被噪声破坏,因为在频率选择过程中,我们只将颜色与输入解耦,而没有积极地去除噪声。引导滤波步骤的目的是去噪。
引导滤波背后的原理主要是 y L y_L yL, y α y_α yα和 y β y_β yβ的信噪比不同。亮度信号 y L y_L yL,根据定义,它是RGB信号的均值,也就是 y L = ( y r + 2 y g + y b ) / 4 y_L=(y_r+2y_g+y_b)/4 yL=(yr+2yg+yb)/4。这种方法可以更好地抑制噪声。与其独立地对三个通道进行去噪,或者将它们作为一个光谱体进行联合去噪,不如先对亮度通道进行去噪,然后使用恢复的亮度信号来指导色度信号的滤波。
基于这种直觉,我们使用了三个深度网络,如图 4.12 所示。亮度去噪网络是一个标准的 UNet ,层数如图 4.12 中间所示。在这个亮度网络的基础上,我们引入了两个较小的 UNet 用于色度通道。色度通道 UNet 的大小是亮度通道 UNet 的 1 4 \frac{1}{4} 41。在训练网络时,我们提取亮度 UNet 编码器生成的特征,并与色度 UNet 生成的相应特征进行拼接。色度 UNet 受益于这种特征共享,因为它们可以使用亮度去噪器中的高频信息,如边缘和纹理。所有三个 UNet 的层都是卷积层,卷积核大小为 3 × 3。所有图像尺度上的特征通道数量都保持固定,以避免不必要的网络大小增加。我们用不可训练的双线性上采样层替换了标准 UNet 中的可训练转置卷积层,以减少总参数数量。
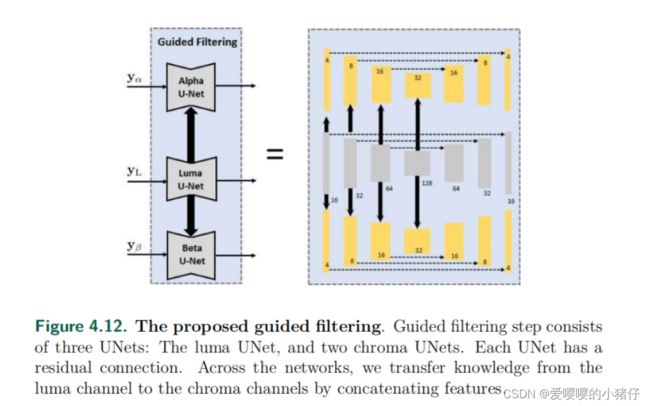
所提出方法的有效性可以从图4.13中直观地看出。

损失函数
为了端到端可训练,我们定义总的损失函数为:

其中, f Θ f_{\Theta} fΘ表示由 Θ \Theta Θ参数化的模型。总的损失函数包括了三个方面。
RGB损失被定义为一个平均绝对误差(mean absolute error,MAE)损失和感知损失的总和。MAE损失是预测图像 f Θ ( y C F A ) f_Θ(y_{CFA}) fΘ(yCFA)和真实图像 x r g b x_{rgb} xrgb之间的 l 1 l_1 l1损失,而感知损失是使用预先训练的网络嵌入的特征之间的 l 2 l_2 l2损失。从直觉上看,如果我们的网络表现良好,那么重建图像的特征就应该接近于干净图像的特征。在这里,这些特征是从VGG-19网络中获得的,尽管也可以使用其他嵌入方式。
亮度和色度损失分别定义为预测亮度值和真实值之间的 l 1 l_1 l1损失,以及预测色度值和真实值之间的 l 1 l_1 l1损失。根据经验选择了超参数 η 1 η_1 η1, η 2 η_2 η2来最小化验证损失。
实现
该模型的训练基于WED数据库,该数据库包含4744张高质量的自然场景彩色图像。彩色图像使用Bayer CFA进行马赛克处理。我们对每个补丁随机模拟平均1到10个光子。我们还通过将标准差设为 0.25 e − 0.25e^- 0.25e−来模拟读出噪声的零均值高斯。然后通过除以平均光子计数并剪切到[0,1]来将图像归一化到[0,1]的范围内。
在每次训练时期,从每张图像中随机裁剪出128×128的补丁,并通过水平和垂直方向的随机翻转进行数据增强。干净和噪声补丁对以64的批量大小输入网络进行训练。网络在混合精度下使用NVIDIA GeForce RTX 2080 GPU(8GB内存)训练共1000个epoch。使用Adam进行优化,前500个epoch和后500个epoch的学习率分别为 1 0 − 4 10^{-4} 10−4和 1 0 − 5 10^{-5} 10−5。
训练超参数为 η 1 = 1 , η 2 = 1 η_1 = 1,η_2 = 1 η1=1,η2=1。可训练的低通滤波器 g ( m , n ) g(m,n) g(m,n)使用7×7内核建模。感知损失基于在VGG-19网络的第8层和第35层计算的MSE损失。在训练期间进行验证时,我们每50个epoch,计算McMaster数据集上的18张彩色图像的平均PSNR和SSIM。
4.3.3实验结果
BURST RECONSTRUCTION WITH QUANTA IMAGE SENSORS
对动态场景建图是一个困难的任务。burst reconstruction是相机用来解决这个问题的标准解决方案之一。这个想法是,如果我们在较短的积分时间内获取多个帧,每一帧都会很尖锐并且有噪声(此时模糊较少),我们可以通过结合多帧的方法来处理噪声。当噪声太大时,将burst合并成单一图像的性能就会受到影响。所以在噪声和模糊之间存在权衡。
当使用QIS成像时,特别是使用低位(bit)的QIS时,处理噪声和运动(模糊)的问题不可避免。所以,我们需要同时处理噪声和运动。这里的主要问题是它们交织在一起。为了去除动态场景中的噪声,我们通常需要对齐帧或者在时空体积上构造一个课可控制的内核。对齐步骤大致相当于光流,构造可操纵核相当于非局部均值或核预测。然而,如果图像受到噪声的污染,光流和核估计都会失败。当这一步失败时,去噪就会变得很困难,因为我们将不容易找到邻近的patch进行滤波。
有QIS burst解决方案需要数百帧来重建。然而,我们还不清楚如何使用更少的帧(< 10帧)进行重建。去噪文献中现有的算法通常只能处理噪声或运动。例如,核预测网络( kernel prediction network,KPN)可以从动态场景中提取运动信息,但当噪声变得很大时,其性能会下降。同样,针对静态场景设计了残余编解码器网络REDNet和DnCNN。在图5.1中,我们展示了一个合成实验的结果。结果说明了基于运动的KPN和单帧REDNet(sRED)的局限性。我们的目标是利用这两者的优势,开发一个解决方案,可以处理更少的帧,仍然重建足够质量的图像。
5.1 方法
5.1.1 学生-导师学习
该方法的基本思想是利用能够完成比所需任务更容易任务的老师网络来将知识蒸馏到我们想要训练的网络中。具体来说,我们提出了一个特定问题:内核预测网络可以很好地处理干净的图像序列。去噪网络可以很好地处理静态图像序列。有没有一种方法可以利用它们的优势来解决动态低光照环境?
图5.2描述了我们的方法。在这种训练协议中有三个参与者:一个运动教师(基于内核预测),一个去噪教师(基于图像去噪网络)和一个学生,即我们最终将使用的网络。两个老师分别使用各自的成像条件进行预先训练。例如,运动教师使用干净且动态内容的序列进行训练,而去噪教师则使用嘈杂但静态内容的序列进行训练。在培训期间,老师们将把他们的知识传递给学生。在测试期间,只使用学生。

为了从两个教师那里迁移知识,学生被设计成有两个分支——一个分支复制运动教师的结构,另一个分支复制去噪教师的结构。在训练学生时,我们生成了三个版本的训练样本。运动老师看到的训练样本是干净的,只包含运动 x m o t i o n x_{motion} xmotion。去噪老师看到的训练样本中没有运动,但被噪声 x n o i s e x_{noise} xnoise破坏。学生看到含有噪声的动态序列 x m o t i o n + n o i s e x_{motion+noise} xmotion+noise。
由于学生和老师拥有一样的分支,我们可以比较老师和学生提取出的特征。具体地,如果我们记由运动老师提取出来的特征为 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅),学生的运动分支提取出来的特征为 ϕ ^ ( ⋅ ) \hat{\phi}(\cdot) ϕ^(⋅),去噪老师提取出来的特征为 φ ( ⋅ ) \varphi(\cdot) φ(⋅),学生的运动分支提取出来的特征为 φ ^ ( ⋅ ) \hat{\varphi}(\cdot) φ^(⋅)。然后我们可以定义一对感知相似性,其中运动相似性为:

去噪相似性为:

直观地说,这对方程确保了学生分支提取的特征与各自教师提取的特征相似。这些特征可以在良好的条件下被提取出来。如果能做到这一点,我们将有一个很好的表示含噪声的动态样本,因此我们可以做一个更好的重建。
两个学生分支可以被视为自动编码器,将输入图像转换为码字。如图5.2右侧所示,我们有一个“解码器”,它将连接的码字翻译回图像。解码器的损失函数由标准均方误差(mean squared error,MSE)损失给出:

其中f是学生网络,因此 f ( x m o t i o n + n o i s y ) f(x_{motion+noisy}) f(xmotion+noisy)表示估计的图像。总体损失函数是这些损失之和:

其中 λ 1 λ_1 λ1和 λ 2 λ_2 λ2是可调参数。训练网络等同于找到编码器 ϕ ^ \hat{\phi} ϕ^和 φ ^ \hat{\varphi} φ^以及解码器 f f f。
5.1.2 老师和学生网络的选择
运动老师是内核预测网络(KPN)。我们通过删除跳过连接来修改它,以保持编码器保留的信息。此外,我们删除池化层和双线性上采样层,以最大化传输到特征层的信息量。经过这些更改,KPN变成了一个完全卷积-反卷积网络。
我们使用的去噪老师是REDNet 的修改版本,也用于另一种QIS重建方法。为了区分这个单帧REDNet和另一个修改版本(将在实验部分讨论),我们将这个单帧REDNet去噪老师称为sRED。与运动老师一样,我们删除残差连接,因为它们会损害学生-教师学习中的特征迁移。
学生网络有两个编码器和一个解码器。编码器具有与教师相同的架构。解码器是由15层堆叠而成,每层都是128通道上卷积。入口层用于连接运动和去噪特征。
5.2 实验
5.2.1 设置
训练数据
训练数据由两部分组成。第一部分是全局运动。我们使用Pascal VOC 2008 dataset,它包含2000张训练图像。第二部分是关于局部动运动的。我们使用Stanford Background Dataset,其中包含715张带有分割的图像。我们从图像中随机裁剪大小为64×64的patch,作为两个数据集的真值。另外还有500张图像用于验证。我们根据一个连续的随机摄像机运动来移动patch,创建全局运动。相机在连续8帧中移动的像素数从7到35个不等。这样的运动速度大约是1m/s。我们固定背景,使用旋转和平移移动前景,从而构建局部运动。平移的实现和全局运动的实现一样,不过只针对前景中的物体。旋转是通过0-15度的角度旋转物体实现的。
训练老师
运动教师使用一组无噪声的动态序列进行训练。损失函数是提出的均方误差(MSE)损失。使用上述数据集对该网络进行了200个epoch的训练。去噪教师使用一组有噪声但静态的图像进行训练。因此,对于每一个真值序列,我们生成三组序列:运动教师用无噪声动态序列,去噪教师用有噪声的静态图像,学生用有噪声的动态序列。我们注意到,这种数据合成方法适用于我们的问题,因为模拟的QIS数据与真实测量值的统计数据相匹配。
基线(Baselines)
提出的方法与三种现有的动态场景重建方法进行了比较:(i) BM4D ,(ii) Kernel Prediction Network (KPN) [141],以及(iii) REDNet 的修改版本。修改后的版本通过在输入层引入3D卷积来汇集特征,从而将REDNet推广到多帧输入。我们将修改后的版本称为多帧RED (mRED)。请注意,mRED具有残差连接,而sRED(去噪教师)则没有。我们认为mRED是一个更公平的基准,因为它采用8个连续帧而不是单个帧作为输入。对于KPN,原始方法建议使用固定内核大小 K = 5 K = 5 K=5;我们通过定义 K K K为运动所经过的最大像素数来修改设置。
实现
所有网络都是使用Keras和TensorFlow实现的。学生-教师训练采用半退火过程。具体来说,正则化参数 λ 1 λ_1 λ1和 λ 2 λ_2 λ2每25个epoch更新一次,使得 λ 1 λ_1 λ1和 λ 2 λ_2 λ2在前100个epoch内呈指数衰减。在接下来的100个epoch内,将 λ 1 λ_1 λ1和 λ 2 λ_2 λ2设置为0,总损失函数变为 L o v e r a l l = L M S E \mathcal{L}_{overall} = \mathcal{L}_{MSE} Loverall=LMSE。
5.2.2 合成数据集上的实验
5.2.3 真实数据集上的实验
5.2.4 Ablation study
图5.10总结了我们研究的5种配置。Config A是一个普通的基线,其中去噪和运动教师都经过预训练。Config B使用单个编码器而不是两个编码器。Ours-I使用学生-教师设置来训练去噪编码器。Ours-II类似于Ours-I,但我们使用运动教师代替去噪教师。Ours-full使用两位老师。所有网络都使用相同的含噪声的动态序列进行训练。实验使用合成数据进行,光子水平为1 ppp,运动为8帧内28像素。结果总结在表5.1中。


学生-教师训练是否必要?
Config A和B不使用任何老师。与Ours-full相比,Config A和Config B的PSNR值低了超过1dB。即使我们与单个老师进行比较,例如Ours-I,它仍然领先Config B 0.8dB,这意味着学生-教师培训协议对性能产生积极影响。
教师编码器是否提取了有意义的信息?
使用两个预训练编码器和一个可训练解码器的Config A,该网络实现了21.51dB,这意味着某些特征对重建有帮助。但是,与Ours-full相比,它要差得多(23.87dB与21.51dB相比)。由于网络架构相同,性能差距可能是由于训练协议造成的,表明学生-教师设置更适合将知识从教师传递给学生网络。
应该使用哪个老师?
配置Ours-I和Ours-II都只使用一个教师。结果表明,如果我们只使用一个教师,则运动教师比去噪教师略有增益(0.1dB)。然而,如果我们像所提出的方法那样同时使用两个老师,我们会观察到另外0.2dB的改进。因此,两个老师的存在都是有益的。
局限和展望
我们已经证明,即使只有8帧,我们也可以在场景移动和弱光下重建一个好的图像。然而,所提出的方法过于严格,不能用于其他设置。如何所提出的方法能够适应任意数量的帧和位深度是一个很好的方向。如何将动态场景重建与第四章中的颜色重建结合起来,将是一件有趣的事情。这个问题的另一个关键方面是,这些低比特深度重建方法需要快速的输出速率,为此,我们需要使这些方法轻量级,以提高推理速度。我们在这里介绍的学生-教师培训计划是一个令人兴奋的想法。稍后,我们将在第7章中看到如何利用它来进行分类和目标检测。