Leetcode刷题笔记
JAVA解题思路模板
-
- 链表
-
- 思路
- 例题+模板
- 数组
-
- 思路
- 例题+模板
- 字符串
-
- 思路
- 二叉树
-
- 思路
- 动态规划
-
- 思路
- 回溯算法
-
- 思路
- 模板
- BFS算法框架
-
- 思路
- 模板
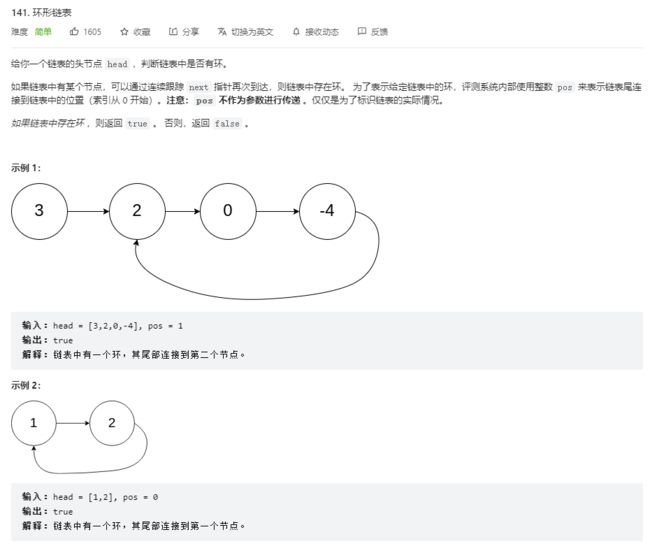
链表
思路
单链表大部分都与双指针有关,看到单链表要想起快慢指针。快慢指针的判断条件要为快指针不为空且快指针的next不为空 (fast != null && fast.next != null)。
例题+模板
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
if(head == null)
return false; //写边界条件
ListNode fast = head, slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
//写判断条件
if(fast == slow)
return true;
}
return false;
}
}
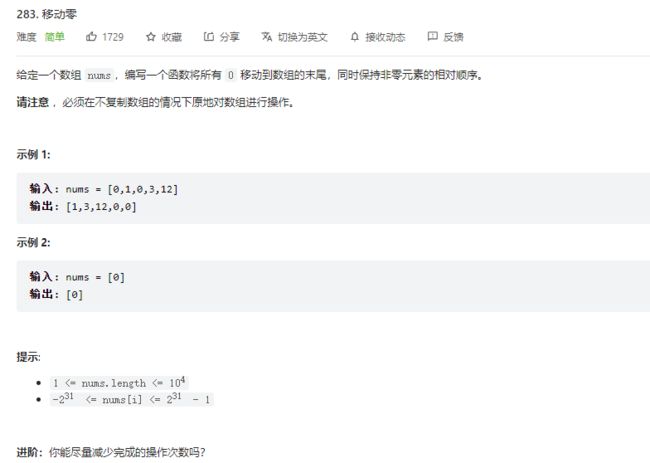
数组
思路
在处理数组和链表相关问题时,双指针技巧是经常用到的,双指针技巧主要分为两类:左右指针和快慢指针。
数组问题中比较常见的快慢指针技巧,是让你原地修改数组和滑动窗口算法。
数组中左右指针的常用题型有二分查找、nSum、反转数组、回文串判断
例题+模板
class Solution {
public void moveZeroes(int[] nums) {
int l = 0, n = nums.length;
for(int r = 0; r < n; r++){
if(nums[r] != 0){
nums[l] = nums[r];
l++;
}
}
while(l < n){
nums[l] = 0;
l++;
}
}
}
字符串
思路
二叉树
思路
二叉树解题的思维模式分两类:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫遍历的思维模式。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫分解问题的思维模式。
无论使用哪种思维模式,你都需要思考:
如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做?
对于经典算法:快速排序和归并排序,我们可以理解为快速排序就是个二叉树的前序遍历,归并排序就是个二叉树的后序遍历。
二叉树的算法思想的运用广泛,甚至可以说,只要涉及递归,都可以抽象成二叉树的问题。
中序位置主要用在 BST(二叉搜索树) 场景中,你完全可以把 BST 的中序遍历认为是遍历有序数组。
前序位置的代码执行是自顶向下的,而后序位置的代码执行是自底向上的。前序位置是刚刚进入节点的时刻,后序位置是即将离开节点的时刻。意味着前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据。
遇到子树问题,首先想到的是给函数设置返回值,然后在后序位置做文章。
快排框架如下:
void sort(int[] nums, int lo, int hi) {
/****** 前序遍历位置 ******/
// 通过交换元素构建分界点 p
int p = partition(nums, lo, hi);
/************************/
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}
归并排序框架如下:
// 定义:排序 nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
int mid = (lo + hi) / 2;
// 排序 nums[lo..mid]
sort(nums, lo, mid);
// 排序 nums[mid+1..hi]
sort(nums, mid + 1, hi);
/****** 后序位置 ******/
// 合并 nums[lo..mid] 和 nums[mid+1..hi]
merge(nums, lo, mid, hi);
/*********************/
}
动态规划
思路
动态规划问题的一般形式就是求最值,求解动态规划的核心问题是穷举。
重叠子问题、最优子结构、状态转移方程就是动态规划三要素。
回溯算法
思路
排列、组合、子集系列问题使用回溯算法,对于数组中可重复的问题要想办法进行剪枝(记得排序)。
模板
组合/子集适用模板:(组合/子集使用start根据位置避免重复选)
List<List<Integer>> res = new LinkedList<>();
// 记录回溯算法的递归路径
LinkedList<Integer> track = new LinkedList<>();
// 主函数
public List<List<Integer>> subsets(int[] nums) {
backtrack(nums, 0);
return res;
}
// 回溯算法核心函数,遍历子集问题的回溯树
void backtrack(int[] nums, int start) {
// 前序位置,每个节点的值都是一个子集
res.add(new LinkedList<>(track));
// 回溯算法标准框架
for (int i = start; i < nums.length; i++) {
// 做选择
track.addLast(nums[i]);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums, i + 1);
// 撤销选择
track.removeLast();
}
}
全排列适用模板:(全排列使用used数组)
List<List<Integer>> res = new LinkedList<>();
// 记录回溯算法的递归路径
LinkedList<Integer> track = new LinkedList<>();
// track 中的元素会被标记为 true
boolean[] used;
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
public List<List<Integer>> permute(int[] nums) {
used = new boolean[nums.length];
backtrack(nums);
return res;
}
// 回溯算法核心函数
void backtrack(int[] nums) {
// base case,到达叶子节点
if (track.size() == nums.length) {
// 收集叶子节点上的值
res.add(new LinkedList(track));
return;
}
// 回溯算法标准框架
for (int i = 0; i < nums.length; i++) {
// 已经存在 track 中的元素,不能重复选择
if (used[i]) {
continue;
}
// 做选择
used[i] = true;
track.addLast(nums[i]);
// 进入下一层回溯树
backtrack(nums);
// 取消选择
track.removeLast();
used[i] = false;
}
}
BFS算法框架
思路
BFS 算法问题本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离。
这个广义的描述可以有各种变体,比如走迷宫,有的格子是围墙不能走,从起点到终点的最短距离是多少?如果这个迷宫带「传送门」可以瞬间传送呢?
再比如说两个单词,要求你通过某些替换,把其中一个变成另一个,每次只能替换一个字符,最少要替换几次?
再比如说连连看游戏,两个方块消除的条件不仅仅是图案相同,还得保证两个方块之间的最短连线不能多于两个拐点。
模板
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj()) {
if (!visited.contains(x)) {
q.offer(x);
visited.add(x);
}
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
//visited 的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有
//子节点到父节点的指针,不会走回头路就不需要 visited。