机器学习笔记之最优化理论与方法(四) 凸函数:定义与基本性质
机器学习笔记之最优化理论与方法——再回首:凸函数定义与基本性质
- 引言
-
- 凸函数的定义
-
- 严格凸函数
- 凸函数的推论:凹函数
- 常见凸函数
- 凸函数的基本性质
- 几种保持函数凸性的运算
- 凸集与凸函数之间的关联关系
引言
本节将介绍凸函数定义及其基本性质。
本文是关于梯度下降法:凸函数 VS \text{VS} VS强凸函数的逻辑补充。涉及的证明过程如:
- 凸函数的一阶条件;
- 凸函数的梯度单调性;
- 凸函数的二阶条件
详见上述链接。
凸函数的定义
关于凸函数的基本定义表示如下:
假设 C \mathcal C C是非空凸集, f ( ⋅ ) f(\cdot) f(⋅)是定义在 C \mathcal C C上的函数,如果对于 ∀ x , y ∈ C \forall x,y \in \mathcal C ∀x,y∈C且 α ∈ ( 0 , 1 ) \alpha \in (0,1) α∈(0,1),均有:
关于凸集的概念、基本性质、凸组合详见凸集的简单认识。
f [ α ⋅ x + ( 1 − α ) ⋅ y ] ≤ α ⋅ f ( x ) + ( 1 − α ) ⋅ f ( y ) f[\alpha \cdot x + (1 - \alpha) \cdot y] \leq \alpha \cdot f(x) + (1 - \alpha) \cdot f(y) f[α⋅x+(1−α)⋅y]≤α⋅f(x)+(1−α)⋅f(y)
则称函数 f ( ⋅ ) f(\cdot) f(⋅)为凸集 C \mathcal C C上的凸函数。
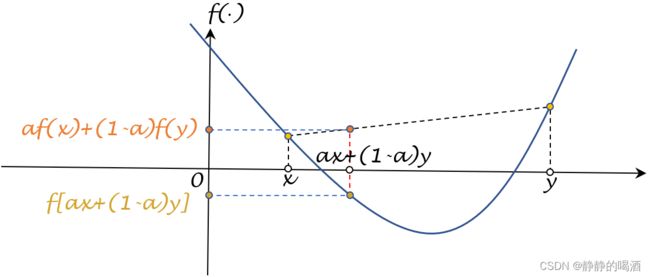
- 观察不等式左侧:其中 α ⋅ x + ( 1 − α ) ⋅ y \alpha \cdot x + (1 - \alpha) \cdot y α⋅x+(1−α)⋅y是点 x , y x,y x,y的凸组合,也就是连接点 x , y x,y x,y的线段上的点;而 f [ α ⋅ x + ( 1 − α ) ⋅ y ] f[\alpha \cdot x + (1 - \alpha) \cdot y] f[α⋅x+(1−α)⋅y]则表示连接点 x , y x,y x,y线段上点的函数值。
- 观察不等式右侧:同左侧,它描述的是:点 f ( x ) , f ( y ) f(x),f(y) f(x),f(y)的凸组合,并始终满足小于等于的关系。
凸函数的几何意义解释如下图所示:
很明显,橙色点相比于黄色点对应的函数值要小。当x , y x,y x,y两点重合时,上式取等。
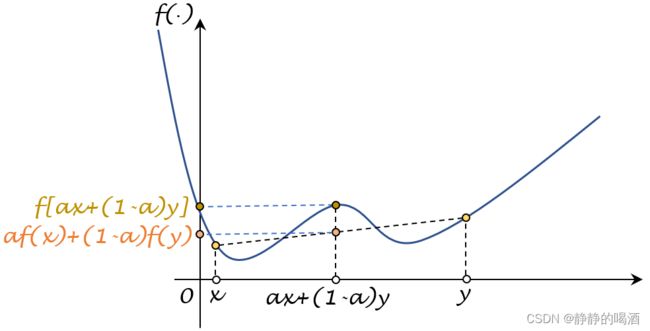
相反,某函数的函数图像表示如下:
在x , y x,y x,y这种取值的情况下,并不满足上述函数。因而该函数不是一个凸函数。
严格凸函数
严格凸函数是在凸函数的基础上增加了相关要求。它的定义方式仅将凸函数的定义修改为:
从而对 x , y ∈ C x,y \in \mathcal C x,y∈C条件下增加了新的要求:点 x , y x,y x,y不能重合。
f [ α ⋅ x + ( 1 − α ) ⋅ y ] < α ⋅ f ( x ) + ( 1 − α ) ⋅ f ( y ) f[\alpha \cdot x + (1 - \alpha) \cdot y] < \alpha \cdot f(x) + (1 - \alpha) \cdot f(y) f[α⋅x+(1−α)⋅y]<α⋅f(x)+(1−α)⋅f(y)
很明显,上面描述的第一个图像对应的函数是严格凸函数;相反:什么样的函数是凸函数,但不是严格凸函数 ? ? ?例如线性函数 f ( x ) = x f(x) = x f(x)=x,它的函数图像就是一条直线:
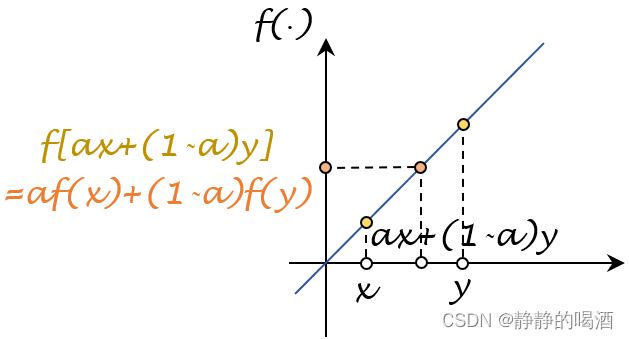
上述函数完全满足凸函数的定义;但不满足严格凸函数的定义。
凸函数的推论:凹函数
如果从定义的角度表述,那么凹函数的定义方式仅将凸函数的定义修改为:
其他条件不变~
f [ α ⋅ x + ( 1 − α ) ⋅ y ] ≥ α ⋅ f ( x ) + ( 1 − α ) ⋅ f ( y ) f[\alpha \cdot x + (1 - \alpha) \cdot y] \geq \alpha \cdot f(x) + (1 - \alpha) \cdot f(y) f[α⋅x+(1−α)⋅y]≥α⋅f(x)+(1−α)⋅f(y)
同上,凹函数的函数图像示例如下:

从凸函数的角度观察,可以得到推论:若 − f ( ⋅ ) -f(\cdot) −f(⋅)是凸函数,则 f ( ⋅ ) f(\cdot) f(⋅)是凹函数。
延伸:如果是关于凹函数 f ( x ) f(x) f(x)的优化问题,如 max f ( x ) \max f(x) maxf(x);可以将其转化为相应凸函数的优化问题: min − f ( x ) \min -f(x) min−f(x)。
常见凸函数
常见凸函数有如下几种:
- 线性函数: f ( x ) = A T x + b f(x) = \mathcal A^T x + b f(x)=ATx+b;需要注意的是:线性函数是唯一一类既是凸函数,也是凹函数的函数。
- 二次函数:它由二次型 x T Q x x^T\mathcal Q x xTQx与线性函数 A T x + b \mathcal A^Tx + b ATx+b组成:
f ( x ) = x T Q x + A T x + b f(x) = x^T \mathcal Q x + \mathcal A^Tx + b f(x)=xTQx+ATx+b
其中 Q ∈ S + n \mathcal Q \in \mathcal S_{+}^n Q∈S+n。在凸集的简单认识(上)中介绍过, S + n \mathcal S_{+}^n S+n描述的可行域是半定矩阵锥:所有 n n n阶半正定矩阵组成的集合:
其中集合S n \mathcal S^n Sn描述所有 n n n阶对称矩阵组成的集合。
S + n { X ∈ S n ∣ X ≽ 0 } \mathcal S_{+}^n \{\mathcal X \in \mathcal S^n \mid \mathcal X \succcurlyeq 0\} S+n{X∈Sn∣X≽0}
并且 S + n \mathcal S_{+}^n S+n是一个凸集;也就是说:矩阵 Q \mathcal Q Q必然至少是一个半正定矩阵。相反,如果对称矩阵 Q \mathcal Q Q的特征值存在负值(如不定矩阵)甚至是负定矩阵,那么对应二次型 x T Q x x^T \mathcal Qx xTQx展开后其二次项系数可能是负值,对应的二次函数就不是凸函数。 - 最小二乘函数:在线性回归一节中介绍了最小二乘法 ( Least Square Method ) (\text{Least Square Method}) (Least Square Method):它通常在线性回归任务中描述模型预测结果与真实标签之间差异性的考量:
L ( W ) = ∑ i = 1 N ∥ W T x ( i ) − y ( i ) ∥ 2 2 \mathcal L(\mathcal W) = \sum_{i=1}^N \|\mathcal W^T x^{(i)} - y^{(i)}\|_2^2 L(W)=i=1∑N∥WTx(i)−y(i)∥22
其中 ( x ( i ) , y ( i ) ) ∈ D = { ( x ( i ) , y ( i ) ) } i = 1 N (x^{(i)},y^{(i)}) \in \mathcal D = \{(x^{(i)},y^{(i)})\}_{i=1}^N (x(i),y(i))∈D={(x(i),y(i))}i=1N。而最小二乘函数定义为如下形式:
f ( x ) = ∥ A x − b ∥ 2 2 f(x) = \|\mathcal Ax - b\|_2^2 f(x)=∥Ax−b∥22
实际上,该函数可将其描述为二次函数:
f ( x ) = ∥ A x − b ∥ 2 2 = ( A x − b ) T ( A x − b ) = ( A x ) T A x − b T A x − ( A x ) T b + b T b = x T A T A x + b T A x − x T A T b + b T b \begin{aligned} f(x) & = \|\mathcal A x - b\|_2^2 \\ & = (\mathcal Ax - b)^T (\mathcal A x - b) \\ & = (\mathcal Ax)^T \mathcal Ax - b^T\mathcal Ax - (\mathcal Ax)^T b + b^Tb \\ & = x^T \mathcal A^T \mathcal A x + b^T \mathcal Ax - x^T \mathcal A^T b + b^T b \\ \end{aligned} f(x)=∥Ax−b∥22=(Ax−b)T(Ax−b)=(Ax)TAx−bTAx−(Ax)Tb+bTb=xTATAx+bTAx−xTATb+bTb
很明显,对应上式中的二次型是: x T A T A x x^T \mathcal A^T \mathcal A x xTATAx,而矩阵 A T A \mathcal A^T \mathcal A ATA必然至少是一个半正定矩阵。因此:最小二乘函数一定是凸函数。 - m m m范数函数:在正则化——拉格朗日乘数法角度中介绍过明可夫斯基距离 ( Minikowski Distance ) (\text{Minikowski Distance}) (Minikowski Distance)。关于向量 x ( i ) ∈ R p x^{(i)} \in \mathbb R^p x(i)∈Rp与 p p p维空间原点之间的明可夫斯基距离表示如下:
∥ x ( i ) ∥ p = [ ∑ k = 1 p ∣ x k ( i ) − 0 ∣ m ] 1 m \|x^{(i)}\|_p = \left[\sum_{k=1}^p |x_k^{(i)} - 0|^m\right]^{\frac{1}{m}} ∥x(i)∥p=[k=1∑p∣xk(i)−0∣m]m1
可以将上述函数描述为关于向量 x ( i ) x^{(i)} x(i)的函数 f [ x ( i ) ] f[x^{(i)}] f[x(i)]:
f ( x ) = [ ∑ k = 1 p ∣ x k ∣ m ] 1 m f(x) = \left[\sum_{k=1}^p |x_k|^m\right]^{\frac{1}{m}} f(x)=[k=1∑p∣xk∣m]m1
其中关于 m ≥ 0 m \geq 0 m≥0时,函数 f ( x ) f(x) f(x)在 m m m不同取值的函数图像示例表示如下:
其中当m = 0 m=0 m=0时,f ( x ) = ∥ x ∥ 0 f(x) = \|x\|_0 f(x)=∥x∥0即x x x非零分量的个数。它是一个非凸函数~
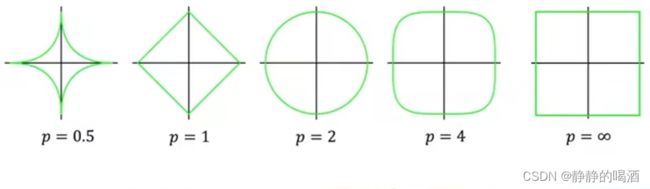
根据凸函数定义可以看出:当 m ≥ 1 m \geq 1 m≥1时,该函数是凸函数;该函数围城的区域是凸集。因而,在 m ≥ 1 m \geq 1 m≥1时, m m m范函数才是凸函数。
凸函数的基本性质
-
如果 f ( x ) f(x) f(x)是凸函数,那么 f ( x ) f(x) f(x)自身在其定义域内一定是连续函数。
-
如果 f ( x ) f(x) f(x)是凸函数 ⇔ ∀ x , y ∈ R n \Leftrightarrow \forall x,y \in \mathbb R^n ⇔∀x,y∈Rn,一元函数 ϕ ( α ) \phi(\alpha) ϕ(α)表示如下:
ϕ ( α ) = f ( x + α ⋅ y ) \phi(\alpha) = f(x + \alpha \cdot y) ϕ(α)=f(x+α⋅y)
并且该函数是凸函数。如果从几何意义的角度解释:由于向量 x , y x,y x,y已知,那么向量 x + α ⋅ y x + \alpha \cdot y x+α⋅y可看作是:从向量 x x x所在位置出发,沿着向量 y y y的方向,移动一段距离后的向量结果。只不过这个距离由 α \alpha α控制。对应图像表示如下:
如果α \alpha α是负值,相当于沿着向量 y y y的反方向移动相应的距离。下图中的y y y更多表示移动的方向;而α ∈ R \alpha \in \mathbb R α∈R控制移动的距离。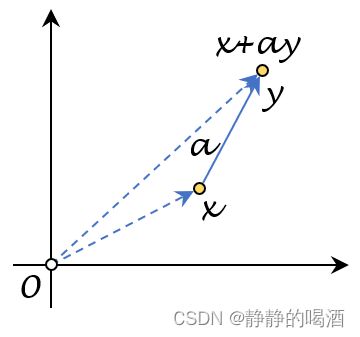
那么关于 ϕ ( α ) = f ( x + α ⋅ y ) \phi(\alpha) = f(x + \alpha \cdot y) ϕ(α)=f(x+α⋅y)它的函数图像示例如下:
其中黄色平面描述 x + α ⋅ y x + \alpha \cdot y x+α⋅y的函数图像,而f ( x + α ⋅ y ) f(x + \alpha \cdot y) f(x+α⋅y)则表示x + α ⋅ y x+\alpha \cdot y x+α⋅y的函数图像与凸函数 f ( ⋅ ) f(\cdot) f(⋅)对应函数图像切面产生的图像黄色虚线,可以看出,这个切面图像也是一个凸函数。

-
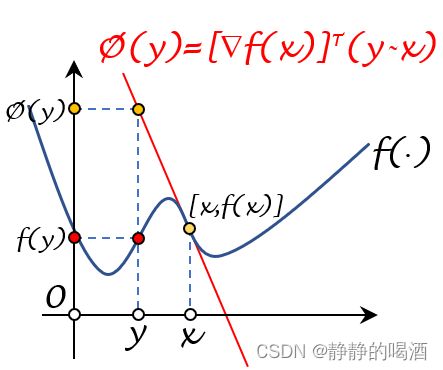
凸函数的一阶条件: f ( x ) f(x) f(x)是 C \mathcal C C上的凸函数充要条件是:
f ( y ) ≥ f ( x ) + [ ∇ f ( x ) ] T ( y − x ) ∀ x , y ∈ C f(y) \geq f(x) + [\nabla f(x)]^T (y - x) \quad \forall x,y \in \mathcal C f(y)≥f(x)+[∇f(x)]T(y−x)∀x,y∈C
该条件的几何图像描述表示如下:
假设将x x x固定住,此时∇ f ( x ) \nabla f(x) ∇f(x)是一个常量,它表示函数 f ( ⋅ ) f(\cdot) f(⋅)在 x x x点处的斜率从而不等式右侧是关于y y y的一次函数,并且经过点 [ x , f ( x ) ] [x,f(x)] [x,f(x)]。可以发现:f ( y ) f(y) f(y)的图像总是在 ϕ ( y ) \phi(y) ϕ(y)的上方(可以重合)。

相反,非凸函数并不具备这个性质。示例如下:
此时f ( y ) < ϕ ( y ) f(y) < \phi(y) f(y)<ϕ(y)。
其证明过程见开头链接,这里不再赘述。 -
凸函数的二阶条件:假设 C ⊂ R n \mathcal C \sub \mathbb R^n C⊂Rn是非空开凸集,并且函数 f ( x ) f(x) f(x)在 C \mathcal C C上二阶连续可微,则有:
f ( x ) is Convex ⇔ ∇ 2 f ( x ) ≽ 0 , ∀ x ∈ C f(x)\text{ is Convex } \Leftrightarrow \nabla^2 f(x) \succcurlyeq 0, \forall x \in \mathcal C f(x) is Convex ⇔∇2f(x)≽0,∀x∈C
如果 x x x是一个标量,那么它关于函数 f ( ⋅ ) f(\cdot) f(⋅)在 x x x点处的 Hessian Matrix ⇒ ∇ 2 f ( x ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(x) Hessian Matrix⇒∇2f(x)则退化成二阶导数 f ′ ′ ( x ) f''(x) f′′(x)。这意味着: f ′ ′ ( x ) ≥ 0 ⇒ f ′ ( x ) f''(x) \geq 0 \Rightarrow f'(x) f′′(x)≥0⇒f′(x)的变化率随着 x x x的增加,处于一个增加/稳定的状态。同上,这里的证明见开头链接,这里不再赘述。
几种保持函数凸性的运算
在函数 f ( x ) f(x) f(x)是凸函数的基础上,对 f ( x ) f(x) f(x)执行一些运算/变换,运算结果其凸函数性质保持不变。
- 透视函数 ( Perspective Function ) (\text{Perspective Function}) (Perspective Function):若 f ( x ) f(x) f(x)是凸函数, x ∈ R n x \in \mathbb R^n x∈Rn。令:
此时G ( ⋅ ) \mathcal G(\cdot) G(⋅)函数内的变量有n + 1 n+1 n+1个。
G ( x , t ) = t ⋅ f ( x t ) t > 0 \mathcal G(x,t) = t \cdot f \left(\frac{x}{t} \right) \quad t > 0 G(x,t)=t⋅f(tx)t>0
则 G ( x , t ) \mathcal G(x,t) G(x,t)也是凸函数。
这里假设 f ( x ) f(x) f(x)是一元函数,且 f ( x ) = x 2 f(x) = x^2 f(x)=x2,那么对应的 G ( x , t ) = x 2 t \begin{aligned}\mathcal G(x,t) = \frac{x^2}{t}\end{aligned} G(x,t)=tx2。该二元函数对应的函数图像表示如下:
即虚线描述的范围,如一个展开的光幕~凑合看吧。其中[ 0 , 1 ] [0,1] [0,1]的部分这里没有表示~

- 非负组合:若 f i ( x ) ( i = 1 , 2 , ⋯ , m ) f_i(x)(i=1,2,\cdots,m) fi(x)(i=1,2,⋯,m)均是凸函数,对于 W i ≥ 0 ( i = 1 , 2 , ⋯ , m ) \mathcal W_i \geq 0(i=1,2,\cdots,m) Wi≥0(i=1,2,⋯,m),有:
G ( x ) = ∑ i = 1 m W i ⋅ f i ( x ) \mathcal G(x) = \sum_{i=1}^m \mathcal W_i \cdot f_i(x) G(x)=i=1∑mWi⋅fi(x)
那么 G ( x ) \mathcal G(x) G(x)是凸函数。
可以观察 G ( x ) \mathcal G(x) G(x)函数在 x x x点处的 Hessian Matrix ⇒ ∇ 2 G ( x ) \text{Hessian Matrix} \Rightarrow \nabla^2 \mathcal G(x) Hessian Matrix⇒∇2G(x):
∇ 2 G ( x ) = ∑ i = 1 m W i ⋅ ∇ 2 f i ( x ) \nabla^2 \mathcal G(x) = \sum_{i=1}^m \mathcal W_i \cdot \nabla^2 f_i(x) ∇2G(x)=i=1∑mWi⋅∇2fi(x)
很明显, ∇ 2 f i ( x ) ( i = 1 , 2 , ⋯ , m ) \nabla^2 f_i(x)(i=1,2,\cdots,m) ∇2fi(x)(i=1,2,⋯,m)必然是半正定的;各 ∇ 2 f i ( x ) \nabla^2 f_i(x) ∇2fi(x)对应的线性组合 ( W i ≥ 0 ) (\mathcal W_i \geq 0) (Wi≥0),其最终结果必然也是半正定的。 - 一组凸函数求最大值:已知 f i ( x ) ( i = 1 , 2 , ⋯ , m ) f_i(x)(i=1,2,\cdots,m) fi(x)(i=1,2,⋯,m)是凸函数,有:
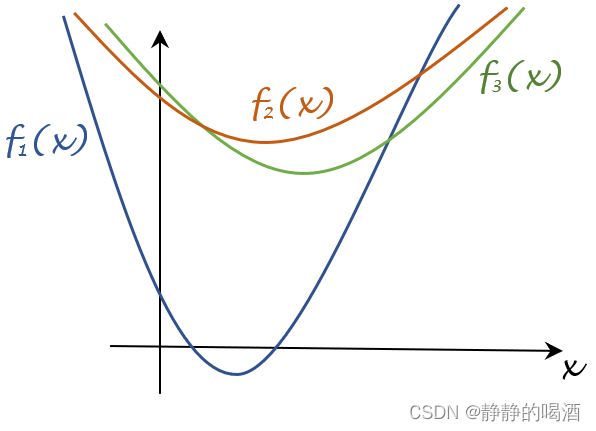
G ( x ) = max { f i ( x ) } i = 1 , 2 , ⋯ , m \mathcal G(x) = \max \{f_i(x)\} \quad i=1,2,\cdots,m G(x)=max{fi(x)}i=1,2,⋯,m
那么 G ( x ) \mathcal G(x) G(x)是凸函数。示例图像表示如下:
求最大值实际上是求交集的一种情况。
凸集与凸函数之间的关联关系
-
工具 1 1 1 - 水平集。其定义对应数学符号描述表示如下:
L a = { x ∣ f ( x ) ≤ a , x ∈ C } \mathcal L_a = \{x \mid f(x) \leq a,x \in \mathcal C\} La={x∣f(x)≤a,x∈C}
任意函数都可以定义水平集,其中 a a a被称作水平值。以二元凸函数为例,给定水平集 a a a,相当于水平集所描述平面横截二元函数图像,并将处在水平集下方的函数图像进行投影。对应图像表示如下:
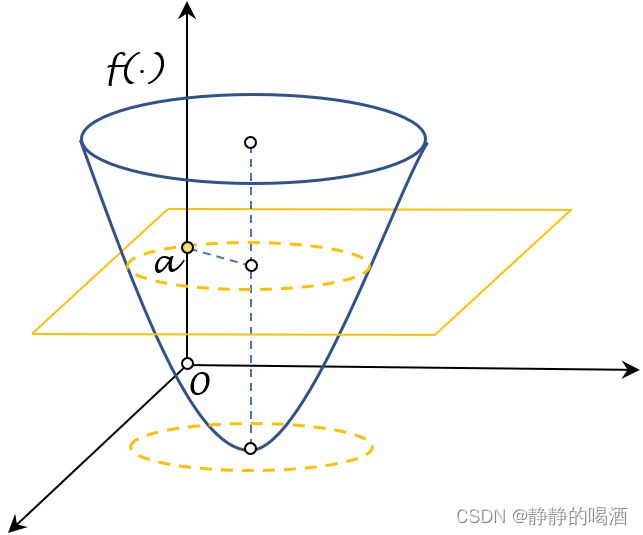
可以明显观察到:投影产生的集合明显是一个凸集。可以使用凸集定义进行证明:- 假设 f ( ⋅ ) f(\cdot) f(⋅)是凸函数,存在值 a a a,其水平集表示为 L a \mathcal L_a La。
- ∀ x , y ∈ L a ; ∀ λ ∈ [ 0 , 1 ] \forall x,y \in \mathcal L_a;\forall \lambda \in [0,1] ∀x,y∈La;∀λ∈[0,1],仅需要判断: λ ⋅ x + ( 1 − λ ) ⋅ y \lambda \cdot x + (1 - \lambda) \cdot y λ⋅x+(1−λ)⋅y是否也在 L a \mathcal L_a La内即可。观察 f [ λ ⋅ x + ( 1 − λ ) ⋅ y ] f[\lambda \cdot x + (1 - \lambda) \cdot y] f[λ⋅x+(1−λ)⋅y]的结果:
f [ λ ⋅ x + ( 1 − λ ) ⋅ y ] ≤ λ ⋅ f ( x ) + ( 1 − λ ) ⋅ f ( y ) f[\lambda \cdot x + (1 - \lambda) \cdot y] \leq \lambda \cdot f(x) + (1 - \lambda) \cdot f(y) f[λ⋅x+(1−λ)⋅y]≤λ⋅f(x)+(1−λ)⋅f(y)
由于 f ( x ) ≤ a f(x) \leq a f(x)≤a且 f ( y ) ≤ a f(y) \leq a f(y)≤a因而 λ ⋅ f ( x ) + ( 1 − λ ) ⋅ f ( y ) ≤ a \lambda \cdot f(x) + (1 - \lambda) \cdot f(y) \leq a λ⋅f(x)+(1−λ)⋅f(y)≤a恒成立。从而 λ ⋅ x + ( 1 − λ ) ⋅ y \lambda \cdot x + (1 - \lambda) \cdot y λ⋅x+(1−λ)⋅y也在 L a \mathcal L_a La内。因而 L a \mathcal L_a La必然是一个凸集。
\quad
相反呢 ? ? ?如果任意取 a a a,函数 f ( x ) f(x) f(x)对应的水平集均是凸集,那么 f ( ⋅ ) f(\cdot) f(⋅)是否为凸函数 ? ? ?不一定。如下图描述的函数:
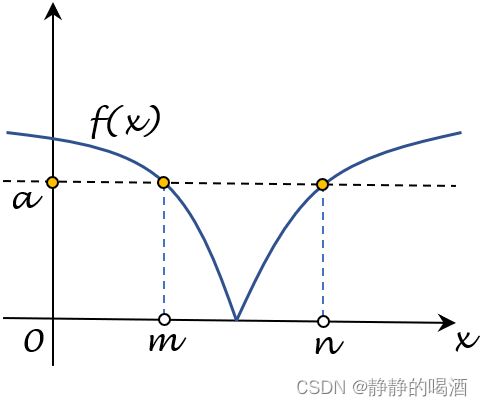
-
工具 2 2 2 - EpiGragh \text{EpiGragh} EpiGragh。关于函数 f ( x ) f(x) f(x)的 EpiGragh \text{EpiGragh} EpiGragh定义表示如下:
Epi ( f ) = { ( x y ) ∣ f ( x ) ≤ y , x ∈ C } \text{Epi}(f) = \left\{\begin{pmatrix}x \\ y\end{pmatrix} \mid f(x) \leq y,x \in \mathcal C \right\} Epi(f)={(xy)∣f(x)≤y,x∈C}
其中 y y y是一个变量,仅满足: f ( x ) ≤ y f(x) \leq y f(x)≤y即可。很明显,若 x ∈ R n x \in \mathbb R^n x∈Rn,那么 ( x y ) \begin{pmatrix}x \\ y\end{pmatrix} (xy)是一个 n + 1 n+1 n+1维向量。而 Epi(f) \text{Epi(f)} Epi(f)就是由该向量组成的集合。如果 f ( x ) f(x) f(x)是一个一维函数,那么它对应的 EpiGragh \text{EpiGragh} EpiGragh示例如下:
由于y y y进满足f ( x ) ≤ y f(x) \leq y f(x)≤y即可,因此阴影部分可以无限向上延伸( y ⇒ ∞ ) (y \Rightarrow \infty) (y⇒∞),这里没有画出来。

其中阴影部分即 Epi(f) \text{Epi(f)} Epi(f)描述的集合。很明显,它比 x x x要高一维。关于 EpiGraph \text{EpiGraph} EpiGraph的一个充要条件:
f ( ⋅ ) is Convex Function ⇔ Epi ( f ) is Convex Set f(\cdot) \text{ is Convex Function} \Leftrightarrow \text{Epi}(f) \text{ is Convex Set} f(⋅) is Convex Function⇔Epi(f) is Convex Set
Reference \text{Reference} Reference:
最优化理论与方法-第三讲-凸函数:定义与基本性质