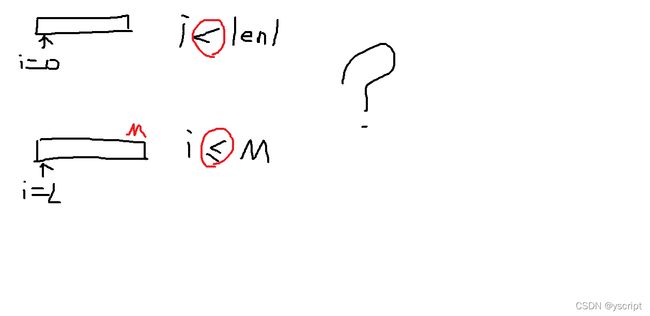详解归并排序
文章目录
- 一、问题引入
- 二、解决
-
- 1.first_merge
-
- 1.1代码分析
- 1.2 first_merge的常见问题
-
- 1.1.1 在函数内使用sizeof(int *p)
- 1.1.2 长度确定的数组作为形参传输时
- 1.1.3遗漏情况
- 三、分治
-
- 1. second_merge
-
- 1.1注释和分析
- 2.和first_merge的区别与联系
- 3.注意问题和容易出错之处
-
- 3.1一些细节问题的个人理解
-
- 3.1.1关于两个指针
- 3.1.2关于等于号
- 四、简化的最终版
一、问题引入
键盘输入两个有序(从小到大)的整数数组(各四个元素),输出两个数组的所有元素,以从小到大的顺序。
样例
输入:
1 5 9 12
2 8 10 11
输出:
1 2 5 8 9 10 11 12
注意:此题算法越优化,分数越高。仅仅AC,只能得基本分60分。
二、解决
1.first_merge
注意,在这道题目中,你当然可以使用冒泡排序AC,但是有比冒泡排序更好的方法。
在这里把问题泛化,将数组长度视为可变。
上代码:
#include1.1代码分析
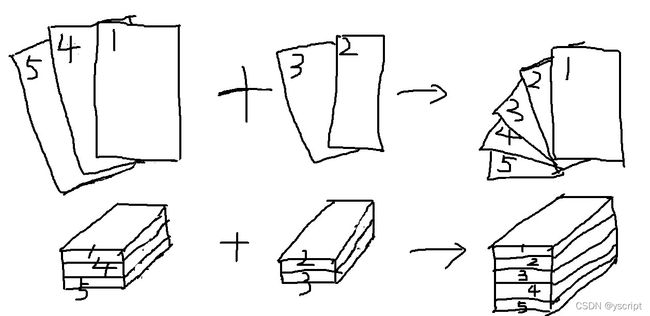
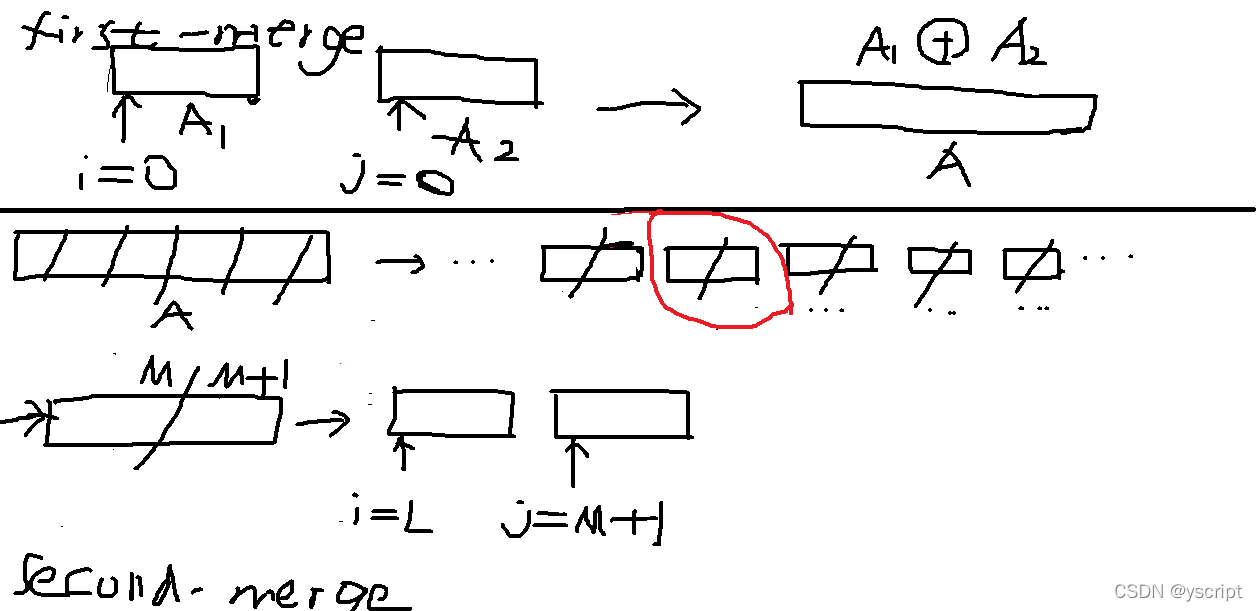
把这种问题类比为两堆已经排好序的牌,做相应的操作使其有序。见下图:
下面是代码注释和分析:
#include1.2 first_merge的常见问题
1.1.1 在函数内使用sizeof(int *p)
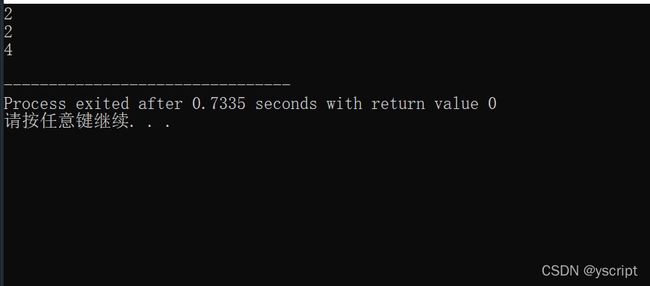
#include结果是这样的:
这是一种很常见的错误,原因是在函数内部使用了sizeof()去求length.
我们加入几行代码:
cout<<len<<endl;
cout<<len1<<endl;
cout<<len2<<endl;
在32位平台下,无论指针的类型是什么,sizeof(指针名)都是4,在64位平台下,无论指针的类型是什么,sizeof(指针名)都是8。
在本程序中,可以看到,不管是什么类型的指针,用sizeof()之后得到的都是8.
而程序的得到的2,2,4,是因为sizeof(int) = 4
8 / 4 = 2
数组名虽然可以视作指针,但对sizeof来说,sizeof(数组名)和sizeof(指针)是不同的。
不管是函数传进去的参数:
void function(int *array);
还是动态内存分配时用的:
int n;
cin>>n;
int *array = new int[n];
sizeof(int *array)得到的都是8;
!注意:只有一个数组arr的长度一开始就被指定好了,sizeof(arr)/sizeof(a[0])才是数组长度
比如:
int array = {1,2,3,4,5,};
或:
void funtion(int array[N]);
解决方法:
1.把数组长度当参数传进去
2.使用全局变量(本题解法)
1.1.2 长度确定的数组作为形参传输时
如果我们希望传参(数组是参数,也就是指针)时按照引用传递;
注意:这里的假设是十分特殊的,就是想用数组的引用
有人会这么写:
...
void function(int *&px);
...
int a[] = {1,2,5,9,14,19};
int *p = a;
function(p);
...
这是没有意义的,因为
int *p = a 这条语句实际上是做了一个指针的赋值,和a = b没有什么差别;
而int *&px = p; 实际上px已经成为p的引用,和数组没有什么关系了,我们希望的是传入数组的引用。
我们需要的是一个指针的引用,或者指向指针的指针。
修改程序为下面的样子:
...
void function(int *&px);
...
int a[] = {1,2,5,9,14,19};
int * & p = a;
function(p);
...
程序还是会提示出错;
[Error] cannot bind non-const lvalue reference of type 'int*&' to an rvalue of type 'int*'
注意这个 ‘non-const’, 数组名a,即数组的首地址是‘不变’的,在编译器眼中为const.
而你实际上声明了一个指针p来作为a的引用,p所指向的对象是可变的,因此是 ‘non-const’.
在编译器眼中,把一个‘non-const’作为’const’的引用是非法的。
改成:
...
void function(int * const &px);
...
int a[] = {1,2,5,9,14,19};
int * const & p = a;
function(p);
...
可以正常运行。
1.1.3遗漏情况
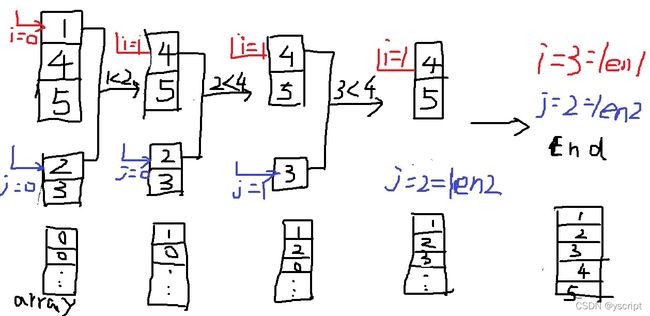
while(i < len1){
array[cnt] = A1[i];
i++;
cnt++;
}
while(j < len2){
array[cnt] = A2[j];
j++;
cnt++;
}
上面的代码特别容易被遗忘,而且不容易发现(因为有可能得到正确的答案)
遗忘后可能出现结果中有 0,0,0这样的数字。
三、分治
1. second_merge
分治是一种非常重要的算法思想,简单来讲就是‘分而治之’,把大的问题切割成小的问题,然后逐个解决。
在first_merge中,我们已经可以做到把两个有序的数组合并成一个新的数组。
现在的新问题是,给一个任意的数组,怎么把它变成有序?
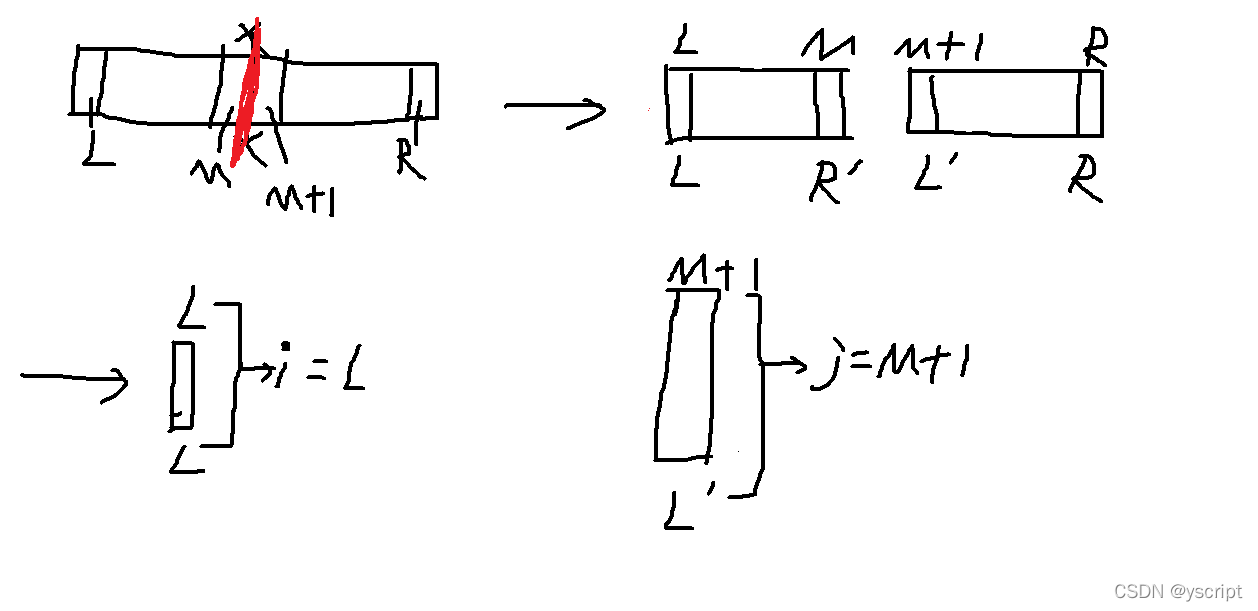
第一步:分——把数组切割,直到每一个小数组有序。
第二步:合——用类似first_merge的方法把一个个有序的数组合并。
既然first_merge针对两个数组,我们就每次把数组切割成两份,最后合并的都是两个两个的数组。
注意:单个的数就是视作有序的!这将是递归的起点。
代码:
#include1.1注释和分析
#include2.和first_merge的区别与联系
看下面两段代码:
一、
int i = 0, j = 0,cnt = 0;
while(i < len1 && j < len2){
if(A1[i] < A2[j]){
array[cnt] = A1[i];
i++;
}
else{
array[cnt] = A2[j];
j++;
}
cnt++;
}
while(i < len1){
array[cnt] = A1[i];
i++;
cnt++;
}
while(j < len2){
array[cnt] = A2[j];
j++;
cnt++;
}
二、
int i = left;
int j = middle + 1;
int cnt = left;
while(i <= middle && j <= right){
if(A[i] < A[j]){
B[cnt] = A[i];
i++;
cnt++;
}else{
B[cnt] = A[j];
j++;
cnt++;
}
}
while(i <= middle){
B[cnt] = A[i];
i++;
cnt++;
}
while(j <= right){
B[cnt] = A[j];
j++;
cnt++;
}
可以看到,两个算法的核心是及其相似的,分治后做类似的first_merge,然后合并、递归,得到对一个数组的归并排序方法。
区别:
区别1.first_merge中,我们使用了i,j两个指针,初始值赋为0,然后比较i与len1,j与len2;
second_merge中,我们使用i,j两个指针,初始值赋为left、middle + 1,然后比较i,j与middle,right.
区别2.first_merge一次就排序完毕,而second_merge中运用了递归,相当与把first_merge做了多次。
区别3.second_merge开辟了一个新的数组B。
3.注意问题和容易出错之处
3.1一些细节问题的个人理解
3.1.1关于两个指针
在first_merge中,i,j两个指针初始化为0,是因为对A1、A2来讲,指针指向的初始位置就是A1和A2头部。
second_merge中,切割后的每个小数组的头部是它对应的left。
因此对一个数组A来说,做一次切割分为两个数组后,有:
3.1.2关于等于号
可以发现,两者是等价的。
四、简化的最终版
#include 文章定有不当之处,还请方家批评指正。