【牛客网题目】合并两个排序的链表
目录
描述
题目分析
描述
输入两个递增的链表,单个链表的长度为n,合并这两个链表并使新链表中的节点仍然是递增排序的。
数据范围:0≤n≤1000,1000≤节点值≤1000
要求:空间复杂度 O(1),时间复杂度 O(n)
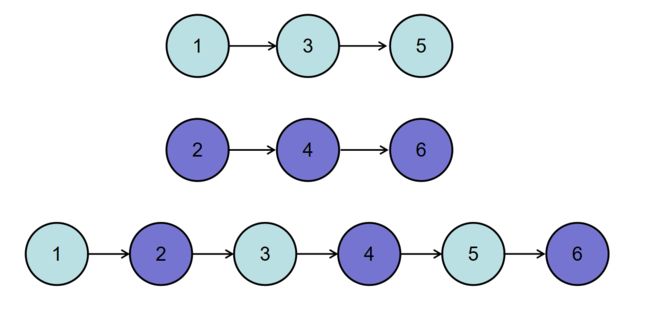
如输入{1,3,5},{2,4,6}时,合并后的链表为{1,2,3,4,5,6},所以对应的输出为{1,2,3,4,5,6},转换过程如下图所示:
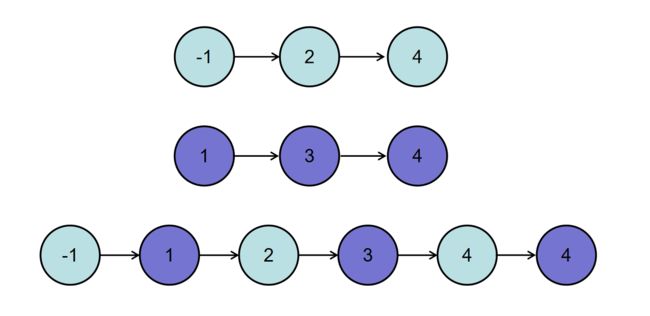
或输入{-1,2,4},{1,3,4}时,合并后的链表为{-1,1,2,3,4,4},所以对应的输出为{-1,1,2,3,4,4},转换过程如下图所示:
示例1
输入:{1,3,5},{2,4,6}
返回值:{1,2,3,4,5,6}示例2
输入:{},{}
返回值:{}示例3
输入:{-1,2,4},{1,3,4}
返回值:{-1,1,2,3,4,4}题目分析
方法一:迭代版本求解
初始化:定义cur指向新链表的头结点
操作:
- 如果l1指向的结点值小于等于l2指向的结点值,则将l1指向的结点值链接到cur的next指针,然后l1指向下一个结点值
- 否则,让l2指向下一个结点值
- 循环步骤1,2,直到l1或者l2为nullptr
- 将l1或者l2剩下的部分链接到cur的后面
技巧
一般创建单链表,都会设一个虚拟头结点,也叫哨兵,因为这样每一个结点都有一个前驱结点。
代码
class Solution {
public:
ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
{
ListNode *vhead = new ListNode(-1);
ListNode *cur = vhead;
while (pHead1 && pHead2) {
if (pHead1->val <= pHead2->val) {
cur->next = pHead1;
pHead1 = pHead1->next;
}
else {
cur->next = pHead2;
pHead2 = pHead2->next;
}
cur = cur->next;
}
cur->next = pHead1 ? pHead1 : pHead2;
return vhead->next;
}
};时间复杂度:O(m+n),m,n分别为两个单链表的长度
空间复杂度:O(1)
方法二:递归版本
方法一的迭代版本,很好理解,代码也好写。但是有必要介绍一下递归版本,可以练习递归代码。
写递归代码,最重要的要明白递归函数的功能。可以不必关心递归函数的具体实现。
比如这个ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
函数功能:合并两个单链表,返回两个单链表头结点值小的那个节点。
如果知道了这个函数功能,那么接下来需要考虑2个问题:
递归函数结束的条件是什么?
递归函数一定是缩小递归区间的,那么下一步的递归区间是什么?
对于问题1.对于链表就是,如果为空,返回什么
对于问题2,跟迭代方法中的一样,如果PHead1的所指节点值小于等于pHead2所指的结点值,那么phead1后续节点和pHead节点继续递归
代码
class Solution {
public:
ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
{
if (!pHead1) return pHead2;
if (!pHead2) return pHead1;
if (pHead1->val <= pHead2->val) {
pHead1->next = Merge(pHead1->next, pHead2);
return pHead1;
}
else {
pHead2->next = Merge(pHead1, pHead2->next);
return pHead2;
}
}
};时间复杂度:O(m+n)
空间复杂度:O(m+n),每一次递归,递归栈都会保存一个变量,最差情况会保存(m+n)个变量