机器学习技术（六）——有监督学习算法之线性回归算法实操

机器学习技术（五）——有监督学习之线性回归算法实操

引言：

机器学习监督算法是一种基于已有标记数据的学习方法，通过对已知输入和输出数据的学习，建立一个模型来预测新的输入数据的输出。这种算法模仿人类的学习过程，从已有的经验中总结规律，并将其应用于新的情况。

本文将介绍有监督学习算法之线性回归的案例实操。

一、线性回归算法实操

通过基于线性回归模型对1960-2010年的年份对全球气温以及二氧化碳排放量的线性关系进行建模以及探索，一共51个数数据点，通过对这51个样本的分析得出两者的线性关系预测。

数据下载地址：https://download.csdn.net/download/tianhai12/88275733

1、实验目的

采用线性回归模型对1960年至2010年年份以及全球温度和二氧化碳排放量的数据进行训练并进行预测。

2、导入相关依赖

#导入相关依赖库
import matplotlib.pyplot as plt
import matplotlib as mpl
import pandas as pd
import seaborn as sns
import sklearn
import numpy as np

3、读取并查看数据

将全球气温数据以及二氧化碳排放量数据进行导入。

#读取数据
co2_df = pd.read_csv('global_co2.csv')
temp_df = pd.read_csv('annual_temp.csv')
#查看前五行数据
print(co2_df.head())
print(temp_df.head())

结果显示如下，二氧化碳排放量共有八个变量。全球气温统计共有GCAG以及GISTEMP两种来源。

  Year  Total  Gas Fuel  Liquid Fuel  Solid Fuel  Cement  Gas Flaring  \
0  1751      3         0            0           3       0            0   
1  1752      3         0            0           3       0            0   
2  1753      3         0            0           3       0            0   
3  1754      3         0            0           3       0            0   
4  1755      3         0            0           3       0            0   

   Per Capita  
0         NaN  
1         NaN  
2         NaN  
3         NaN  
4         NaN  
    Source  Year    Mean
0     GCAG  2015  0.8990
1  GISTEMP  2015  0.8700
2     GCAG  2014  0.7402
3  GISTEMP  2014  0.7500
4     GCAG  2013  0.6687

4、数据清洗

将我们所需数据从原有数据集中提取并重新整合命名。

# 数据清洗
co2_df = co2_df.iloc[:,:2]                     # 只提取CO2的总量和年份数据
co2_df = co2_df.loc[co2_df['Year'] >= 1960]   # 只获取 1960 - 2010年的数据
co2_df.columns=['Year','CO2']                # 重命名列名
co2_df = co2_df.reset_index(drop=True)       # 重新设定索引

# 只保留GCAS一个燃气
temp_df = temp_df[temp_df.Source != 'GISTEMP']                              
# Drop name of source
temp_df.drop('Source', inplace=True, axis=1)                                
# 重置索引
temp_df = temp_df.reindex(index=temp_df.index[::-1])                        
# 只保留 1960 - 2010
temp_df = temp_df.loc[temp_df['Year'] >= 1960].loc[temp_df['Year'] <= 2010]   
# 重命名列
temp_df.columns=['Year','Temperature']                                    
# 重置索引
temp_df = temp_df.reset_index(drop=True)                                  
# 输出前五行
print(co2_df.head())
print(temp_df.head())

结果如下所示，只留下CO2排放量以及来源GCAG的温度统计。

   Year   CO2
0  1960  2569
1  1961  2580
2  1962  2686
3  1963  2833
4  1964  2995
   Year  Temperature
0  1960       0.0252
1  1961       0.0818
2  1962       0.0924
3  1963       0.1100
4  1964      -0.1461

5、合并两个数据集

将数据整合在一起便于后续回归计算。

#整合两个数据表到一个表中
climate_change_df = pd.concat([co2_df, temp_df.Temperature], axis=1)
#打印新数据集的前五行
print(climate_change_df.head())

得到如下结果

 Year   CO2  Temperature
0  1960  2569       0.0252
1  1961  2580       0.0818
2  1962  2686       0.0924
3  1963  2833       0.1100
4  1964  2995      -0.1461

6、数据可视化

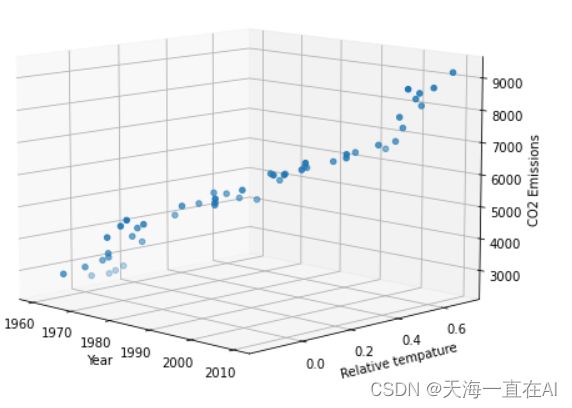
1、绘制3D图

导入所需方法，对年份，二氧化碳排放量以及全球温度构建3D图

#导入绘制3D图像的方法
from mpl_toolkits.mplot3d import Axes3D
#创建画布
fig = plt.figure()
#设定画布大下
fig.set_size_inches(12.5, 7.5)
ax = fig.add_subplot(111, projection='3d')
#绘制散点图
ax.scatter(xs=climate_change_df['Year'], ys=climate_change_df['Temperature'], zs=climate_change_df['CO2'])
#添加xlabel, ylabel,标题
ax.set_ylabel('Relative tempature'); ax.set_xlabel('Year'); ax.set_zlabel('CO2 Emissions')
ax.view_init(10, -45)

得到下图

2、构建折线图

从上图样本点可以看出变量之间一个近似线性的关系，为了更好理解数据分别构建年份与CO2折线图以及年份与温度折线图，相当于将3D拆分为2D。

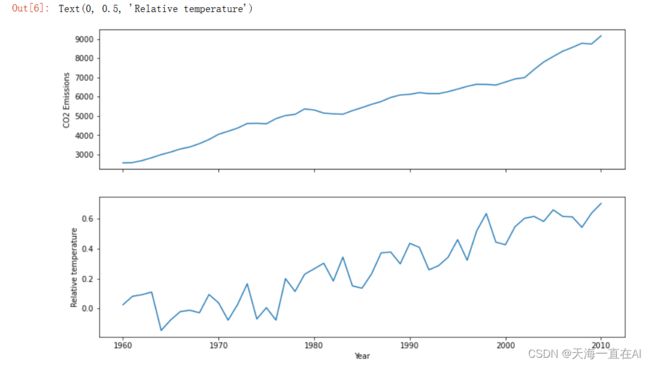
可见二氧化碳排放量随着年份上升，相对平稳上涨。相比之下全球相对温度随着年份上升起伏较大，但总体也呈上升阶段。

7、训练模型并进行可视化

1、划分数据集

划分训练集以及测试集，利用线性回归模型对数据进行建模，并输出可视化图像。

#导入数据集的划分方法
from sklearn.model_selection import train_test_split
#分别给X,Y进行赋值
X = climate_change_df['Year']
X = X.values
X = X.reshape(-1,1)
Y = climate_change_df[['CO2', 'Temperature']].astype('float32')
Y = Y.values
#划分训练集和测试集，test_size参数为指定测试集的比例，此处为10%的数据集设置为测试集。
X_train, X_test, y_train, y_test = np.asarray(train_test_split(X, Y, test_size=0.1))

2、训练模型

导入所需方法并创建模型输出模型测试结果。

#导入线性回归方法
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.metrics import accuracy_score
#创建模型
reg = LinearRegression()
#使用训练集训练模型
reg.fit(X_train, y_train)
#测试集进行测试，并输出模型测试结果
y_pred=list(reg.predict(X_test.reshape(-1, 1)))
#测试集进行测试，并输出模型测试结果
r2_score(y_test, y_pred, multioutput= 'variance_weighted')

每次输出的值都不相同，不过都在0.9以上，说明得分情况比较优秀

3、数据可视化

标准化后进行可视化步骤，对该三维数据形成三维折线图。

#生成数组，并进行标准化
x_line = np.arange(1960,2011).reshape(-1,1)
p = reg.predict(x_line).T
#生成画布
fig2 = plt.figure()
#设置画布大小
fig2.set_size_inches(12.5, 7.5)
ax = fig2.add_subplot(111, projection='3d')
#绘制3D散点图，三个维度分别表示年份，温度和CO2
ax.scatter(xs=climate_change_df['Year'], ys=climate_change_df['Temperature'], zs=climate_change_df['CO2'])
#添加各坐标轴的描述
ax.set_ylabel('Relative tempature'); ax.set_xlabel('Year'); ax.set_zlabel('CO2 Emissions')
#绘制折线图
ax.plot(xs=x_line, ys=p[1], zs=p[0], color='green')
ax.view_init(10, -45)

将两个表现在二维空间的一元线性模型投射于三维空间中的一根直线虽然只有一条直线，但其实x轴和y轴，x轴和z轴形成两个一元线性模型。

分别可视化两个模型为2D

#生成画布
f, axarr = plt.subplots(2, sharex=True)
#设置画布大小
f.set_size_inches(12.5, 7.5)
#绘制第一个折线图，横纵坐标分别为年份和CO2
axarr[0].plot(climate_change_df['Year'], climate_change_df['CO2'])
#在第一个折线图中添加预测的线性回归模型
axarr[0].plot(x_line, p[0])
#添加Y轴的描述
axarr[0].set_ylabel('CO2 Emissions')
#绘制第二个折线图，横纵坐标分别为年份和温度
axarr[1].plot(climate_change_df['Year'], climate_change_df['Temperature'])
#添加预测的模型
axarr[1].plot(x_line, p[1])
#添加X，Y轴的描述
axarr[1].set_xlabel('Year')
axarr[1].set_ylabel('Relative temperature')

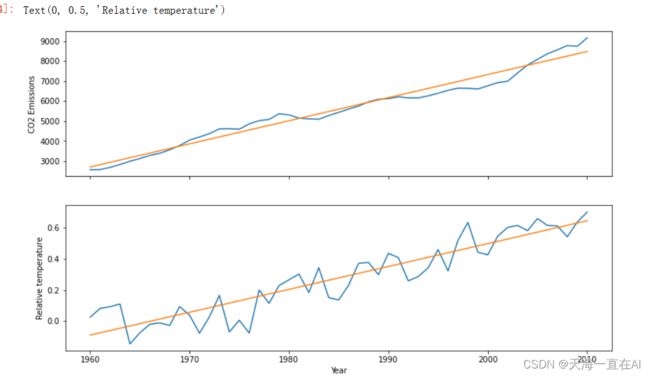
输出分别为年份对于CO2排放量的一元线性回归模型，以及年份对于全球温度的一元线性回归，可以看出，线性模型符合数据趋势，相比之下年份与CO2排放量的模型拟合表现更好。