Java【手撕滑动窗口】LeetCode 438. “字符串中所有异位词“, 图文详解思路分析 + 代码
文章目录
- 前言
- 一、字符串中所有异位词
-
- 1, 题目
- 2, 思路分析
-
- 2.1, 引入哈希表找出异位词
- 2.2, 引入变量记录"有效字符的个数"
- 2.3, left 右移维护窗口
- 2.4, 总结核心步骤
- 3, 代码
前言
各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你:
JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等
Java数据结构: 顺序表, 链表, 堆, 二叉树, 二叉搜索树, 哈希表等
JavaEE初阶: 多线程, 网络编程, TCP/IP协议, HTTP协议, Tomcat, Servlet, Linux, JVM等(正在持续更新)
一、字符串中所有异位词
1, 题目
OJ链接
以示例1为例, 给定字符串 s 为 : "cbaebabacd", 字符串 p 为"abc", "abc"和 "cba", "acb", "bca" 等是异位词, 要求在 s 中找到 p 的所有异位词, 意思就是在 s 中找到连续的子区间, 这段区间是 p 的异位词
- 关于异位词
我们只需要 s 的连续子区间内找到包含 ‘a’, ‘b’, ‘c’ 的三个字符即可, 不一定非要是"abc", 这点很重要 ! !
一般来说, 如果我们研究的对象是 “连续的区间” 就可以考虑滑动窗口
滑动窗口其实就是"同向双指针", 滑动窗口的特点是, 前后两个指针不会回退, 并且窗口总是向前滑动, 窗口不是固定大小的, 可能边长也可能变短, 如果你在分析题目的时候发现了这些特征, 那就基本是滑动窗口的解法了
2, 思路分析
首先可以确定的是, 一定要有两个哈希表, 一个哈希表来记录字符串 p 中的字符出现了几次, 一个哈希表用来记录在字符串 s 的子区间中的字符出现了几次
基本思路 :
- 1, 为了方便, 可以将字符串 s 和 p 分别转化为字符数组 : arrayS 和 arrayP
- 2, 定义两个哈希表, hashP 和 hashWindow
- 3, 定义 left 和 right 指针, 初始位置都从0开始, left 用于标记子序列的左边界, right 用于标记子序列的右边界
题目中说明了字符都是 ‘a’ ~ ‘z’ 的小写字符, 为了进一步提高效率, 可以直接使用长度为 26 的 int[] 数组来模拟哈希表, 用字符来映射出 0~25下标, 例如字符 ‘a’ 在哈希表中的下标就是 ‘a’ - ‘a’ = 0, 字符 ‘c’ 在哈希表中的下标就是 ‘c’ - ‘a’ = 2
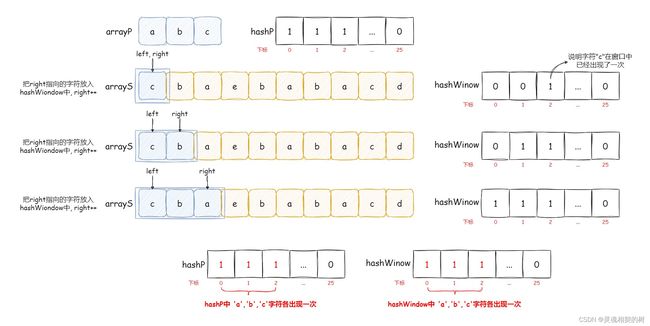
2.1, 引入哈希表找出异位词
首先要把 arrayP (字符串 p 的字符数组) 中的字符在哈希表中映射, 出现几次就把哈希表中对应下标的值设为几
然后在 arrayS (字符串 s 的字符数组) 中找到的字符也在哈希表中映射, 同上
要注意, 使用者两个哈希表的目的是记录 “字符出现的次数”, 而不是"字符出现的个数"
例如要找 “bbc” 的异位词, ‘b’ 在哈希表中出现两次, ‘c’ 在哈希表中出现一次, 重点是字符出现的次数而不是个数
由于我们要找的子区间长度是和字符串 p 长度一致的, 所以要让 right 和 left 维护子区间的长度
此时 right 和 left 维护的子区间的长度和 arrayP 长度一致, 并且我们发现两个哈希表中的所记录的 “字符出现的次数” 是一致的, 那就可以认为我们找到了一个异位词
这里可以做优化 ! ! 如何判断两个哈希表中的所记录的 “字符出现的次数” 是一致的?
如果每次在 arrayS 中找到长度为 3 的子区间都遍历两个 hash 表, 是比较浪费时间的, 我们可以引入一个变量 count 用于记录"有效字符的个数"
2.2, 引入变量记录"有效字符的个数"
首先图解一下什么情况下, 字符为有效, 什么情况下不有效
注意观察不同示例下的 arrayS 和 arrayP

综上所述, right 每遍历到一个新的字符时, 就可以对比两个哈希表中的值来判断该字符是否有效
- 当
hashWindow[arrayS[right] - 'a'] <= hashP[arrayS[right] - 'a']时, 为有效字符, 此时可以让变量 count++ - 当
count == arrayP时, 说明 right 和 left 维护的子区间的字符全都是有效字符, 即全都是 arrayP 中的字符, 此时可以把 left 加入到 list 中, 作为返回结果
2.3, left 右移维护窗口
上面说过, 假设我们要找的异位词的长度为 3 , 那么 right 和 left 维护的子区间(窗口)的长度就不能大于 3, 当窗口长度为 3 时, 判断 count 的值以判断是否为异位词
所以当窗口长度大于 3 时, 需要让 left 右移来实现"滑动窗口", 这一步有值得注意的细节
本题的窗口在"滑动:过程中长度总是为 arrayP.length, 在"滑动窗口"中属于窗口长度不变的类型
2.4, 总结核心步骤
- 1, right 指向新字符时, 在 hashWindow 中更新该字符出现的次数
- 2, 判断 right 指向的字符是否为有效字符, 如果是, 令 count++
- 3, 判断窗口大小是否大于 arrayP.length, 如果是, 令 left–
- 4, 在 left-- 之前判断当前 left 指向的字符是否为有效字符, 如果是, 则 count- -
- 5, 判断 count 是否和 arrayP.length 相等, 如果是, 令当前 left 存入 list 中
3, 代码
public List<Integer> findAnagrams(String s, String p) {
List<Integer> ret = new ArrayList<>();
char[] arrayP = p.toCharArray();
char[] arrayS = s.toCharArray();
int[] hashP = new int[26];
int[] hashWindow = new int[26];
for(char ch : arrayP) {
hashP[ch-'a']++;
}
int left = 0;
int right = 0;
int count = 0;// 有效字符个数
while(right < arrayS.length) {
hashWindow[arrayS[right] - 'a']++;
if(hashWindow[arrayS[right] - 'a'] <= hashP[arrayS[right] - 'a']) {
count++;
}
if(right - left + 1 > arrayP.length) {
// left 右移之前要先判断是否为有效字符
if(hashWindow[arrayS[left] - 'a'] <= hashP[arrayS[left] - 'a']) {
// 说明是有效字符
count--;
}
// hash表里面的该字符也要自减一次
hashWindow[arrayS[left] - 'a']--;
left++;
}
if(count == arrayP.length) {
ret.add(left);
}
right++;
}
return ret;
}