算法题目练习(C/c++/java)
记录做过的经典题型,以便于以后查看
目录
-
- 二分法
-
- 1. 二分查找一个数
- 2. 二分查找左边界
- 3. 二分查找右边界
- 计算最大公约数
-
- 辗转相除
- 递归辗转
- 链表的逆置
- 前缀和求法
-
- 一维前缀和:
- 二维前缀和:
- 包子凑数
- 扩展欧几里得算法:
-
- 例子:青蛙的约会
- dp最长单调子序列
- 判断哪日期合法性
- 快速排序
- 归并排序算法
- 计算时间 按时分秒格式输出
- 树状数组和线段数组
- 三数之和(双指针)
- 滑动窗口
-
- 找异步词
- 乘积小于k的数组
- 岛屿问题详解
-
-
- 基本框架代码 dfs
- 岛屿数量
- 岛屿周长
- 岛屿面积
-
- 图的问题 省份数量(dfs)
- 二叉树的遍历
-
- 先/中/后序遍历
- 层序遍历
- 二叉树最大深度
- 合并二叉树
- 二叉树的镜像
- 判断二叉搜索树
- 判断完全二叉树
- 判断是否是平衡二叉树
- 在二叉树中找到两个节点的最近公共祖先
- 字符串题目练习
-
- 最长前缀
- 字符串排列查找 (用滑动窗口做)
- 大数的乘法(用字符串表示结果)
- 大数加法
- 翻转字符串
- 最长回文串
- 简化路径
- 复原IP地址
- 并查集学习
- 合并有序数组
- 合并区间
- 最长公共子序列
二分法
运用二分法查找的场景:二分查找一个数的位置、 二分查找左边界、二分查找右边界。
1. 二分查找一个数
//二分查找一个数
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
while(left <= right) { // 注意
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
2. 二分查找左边界
//二分法寻找左边界
int find_left(int arr[],int k)
{
int l = 0, r = n;//搜索的区间为[l,r)
while(l<r)
{
int mid = (l+r)/2;
if(arr[mid] >= k)
{
r = mid;//为了找左边界
}
else if(arr[mid] < k)
{
l = mid+1;
}
}
//k比所有数都大了 不存在
if(l==n)
return -1;
return arr[l]==k ? l : -1;
}
3. 二分查找右边界
//二分法找右边界
int find_right(int arr[],int k)
{
int l = 0,r = n;
while(l<r)
{
int mid = (l+r)/2;
if(arr[mid] <= k)
{
l = mid+1;//为了找到右边界
}
else
{
r = mid;
}
}
if(l==0)
return -1;
return arr[l-1]==k ? (l-1) : -1;
}
计算最大公约数
辗转相除
int gcd(int a,int b)
{
int r,t;
if(a<b)
{
t = a;
a = b;
b = t;
}
while (b!=0)
{
r = a%b;
a = b;
b = r;
}
return a;
递归辗转
int gcd(int a,int b)
{//a>b
return b==0 ? a : gcd(b,a%b);
}
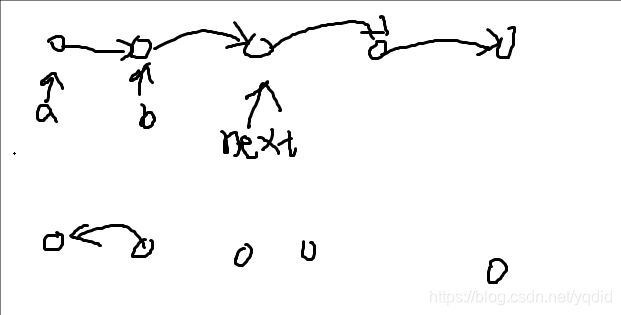
链表的逆置
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head || !head->next) return head;
//迭代的做法
ListNode *a = nullptr;//空指针
ListNode *b = head;
while(b)
{
ListNode *next = b->next;//先把b的下个节点存起
b->next = a;
a = b;
b = next;
}
return a;
}
};
前缀和求法
一维前缀和:
例题:
输入一个长度为 n的整数序列。接下来再输入 m个询问,每个询问输入一对 l,r。 对于每个询问,输出原序列中从第 l个数到第 r 个数的和。
输入样例:
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例
3
6
10
思路:
定义一个sum[] ,sum[i]表示前a数组中i个数相加的和。
求前缀和运算:
const int N=1e5+10;
int sum[N],a[N];
for(int i=1;i<=n;i++)
{
cin>>a[i];
sum[i]=sum[i-1]+a[i];
}
对于每次查询,只需执行 sum[r]-sum[l-1] ,时间复杂度为O(1)
则代码为:
#include
// {
// sum += arr[i];
// }
// return sum;
// }
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>arr[i];
sum[i] = arr[i]+sum[i-1];//直接就加上
}
for(int i=0;i<m;i++)
{
cin>>l>>r;
//cout<
cout<<sum[r]-sum[l-1]<<endl;
}
return 0;
}
二维前缀和:

由图可知:
整个外围蓝色矩形面积s[i][j] = 绿色面积s[i-1][j] + 紫色面积s[i][j-1] - 重复加的红色的面积s[i-1][j-1]+小方块的面积a[i][j];
则二维前缀和的预处理公式:
s[i][j] = s[i-1][j]+s[i][j-1]+a[i][j]-s[i-1][j-1]
求以(x1,y1) 为左上角,(x2,y2)为右下角的矩阵元素的和

s = s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]
包子凑数
欧几里得算法 最大公约数
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)
#include ax+by=c 有整数解 --> c/gcd(a,b)
|
|
扩展欧几里得算法:
即如果a、b是整数,那么一定存在整数x、y使得ax+by=gcd(a,b)
换句话说,如果ax+by=m有解,那么m一定是gcd(a,b)的若干倍。(可以用来判断一个这样的式子有没有解)
详解链接
#include例子:青蛙的约会
#include 中国剩余定理
https://blog.csdn.net/shenmingxueIT/article/details/108537370
dp最长单调子序列
求最长上升子序列
求长度
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
if(a[i]>a[j]) f[i]=max(f[i],f[j]+1);
}
for(int i=1;i<=n;i++) ans=max(ans,f[i]);
判断哪日期合法性
int months[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
bool check(int date)
{
int year = date / 10000;
int month = date % 10000 / 100;
int day = date % 100;
if (!month || month >= 13 || !day) return false;
if (month != 2 && day > months[month]) return false;
if (month == 2)
{
bool leap = year % 4 == 0 && year % 100 || year % 400 == 0;
if (day > 28 + leap) return false;
}
return true;
}
快速排序
void quickSort(vector<int>& arr,int l,int r){
if(l>=r) return;
int i=l,j=r;
int base = arr[i];
while(i<j){
//从后往前找,找到比base小的值
while(arr[j]>=base && i<j) j--;
//从前往后找 找到比base大的值
while(arr[i]<= base && i<j) i++;
//找到符合条件的值 交换
if(i<j){
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
//先挪,然后再把中枢放到指定位置
arr[l] = arr[i];
//修改该位置的数据为base
arr[i] = base;
//递归左右两边
quickSort(arr,l,i-1);
quickSort(arr,i+1,r);
}
优化一点:
思路:
一趟快速排序的算法是:
-
设置两个变量i、j,排序开始的时候:令i=0,j=length-1;
-
以第一个数组元素作为枢轴,赋值给key,即key=array[0];
-
从j开始向前扫描,找到第一个小于key的值array[j],将array[j]和array[i]的值交换;
-
从i开始向后扫描,找到第一个大于key的值array[i],将array[i]和array[j]的值交换;
-
重复第3、4步,直到i==j,将枢轴元素移到正确位置上,即将key赋值给array[i]。
时间复杂度 O(nlogn) 最坏:O(n^2)
void QuickSort(int *array,int low,int high){ //快排
if(low>=high){ //若待排序序列只有一个元素,返回空
return ;
}
int i=low; //i作为指针从左向右扫描
int j=high; //j作为指针从右向左扫描
int key=array[low];//第一个数作为基准数
while(i<j){
while(array[j]>=key&&i<j){ //从右边找小于基准数的元素 (此处由于j值可能会变,所以仍需判断i是否小于j)
j--; //找不到则j减一
}
array[i]=array[j]; //找到则赋值
while(array[i]<=key&&i<j){ //从左边找大于基准数的元素
i++; //找不到则i加一
}
array[j]=array[i]; //找到则赋值
}
array[i]=key; //当i和j相遇,将基准元素赋值到指针i处
QuickSort(array,low,i-1); //i左边的序列继续递归调用快排
QuickSort(array,i+1,high); //i右边的序列继续递归调用快排
}
归并排序算法
时间复杂度:O(nlogn)
思路:
1、一分为二,确定分界点 mid=(l+r)/2
2、递归排序左右区间
3、将左右两边的有序区间合并 用双指针 临时数组存
详细代码如下:
#include计算时间 按时分秒格式输出
只要知道秒数 就可以按以下公式算出 相应的时分秒
//ss为距离0时0分0秒经过的秒数
h=ss/3600;
m=ss/60%60;
s=ss%60;
//输出格式
printf("%02d:%02d:%02d",h,m,s);
例子:
输入格式
一个输入包含多组数据。
输入第一行为一个正整数 T
,表示输入数据组数。
每组数据包含两行,第一行为去程的起降时间,第二行为回程的起降时间。
起降时间的格式如下:
h1:m1:s1 h2:m2:s2 h1:m1:s1 h3:m3:s3 (+1) h1:m1:s1 h4:m4:s4 (+2)第一种格式表示该航班在当地时间h1时m1分s1秒起飞,在当地时间当日h2时m2分s2秒降落。
第二种格式表示该航班在当地时间h1时m1分s1秒起飞,在当地时间次日h2时m2分s2秒降落。
第三种格式表示该航班在当地时间h1时m1分s1秒起飞,在当地时间第三日h2时m2分s2秒降落。
输出格式
对于每一组数据输出一行一个时间hh:mm:ss,表示飞行时间为hh小时mm分ss秒。
注意,当时间为一位数时,要补齐前导零,如三小时四分五秒应写为03:04:05。
数据范围保证输入时间合法(0≤h≤23,0≤m,s≤59 ),飞行时间不超过24小时。
输入样例:
3
17:48:19 21:57:24
11:05:18 15:14:23
17:21:07 00:31:46 (+1)
23:02:41 16:13:20 (+1)
10:19:19 20:41:24
22:19:04 16:41:09 (+1)输出样例:
04:09:05 12:10:39 14:22:05
#include 树状数组和线段数组
三数之和(双指针)
题目:
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
题解:
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
//思路: 先排序,~~然后去重~~ 再找符合条件的三元组
vector<vector<int>> ans;
int n=nums.size();
if(n<3){//长度小于3 无解
return ans;
}
sort(nums.begin(),nums.end());
if(nums[0]>0){//排序后第一个元素大于0 无解
return ans;
}
for(int i=0;i<n;i++)
{
if(nums[i]>0) break;
if(i>0 && nums[i] == nums[i-1]) continue;//去重
int l=i+1,r=n-1;
while(l<r){
int sum = nums[i] + nums[l] + nums[r];
if(sum==0){
// 加入res
ans.push_back({nums[i],nums[l],nums[r]});
while(l<r && nums[l] == nums[l+1]) l++;//去重
while(l<r && nums[r] == nums[r-1]) r--;//去重
l++;
r--;
}
else if(sum<0) l++;
else if(sum>0) r--;
}
}
return ans;
}
};
滑动窗口
找异步词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异步词:字母相同,但排列不同的字符串。
例子:
输入: s = “cbaebabacd”, p = “abc”
输出: [0,6]
解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
// 用ascll值比较异步词
// 因为字符串中的字符全是小写字母,可以用长度为26的数组记录字母出现的次数
vector<int> pcounter(26,0);//记录p字符串的字母频次
vector<int> scounter(26,0);//记录s字符串前m个字母频次
vector<int> res;
int s_len=s.length();
int p_len=p.length(),l=0;//利用l记录异步词出现的位置
for(int i=0;i<p_len;i++){//记录下p的串对应的ascll码在数组的出现的次数 方便比较
pcounter[p[i]-'a']++;
}
for(int i=0;i<s_len;i++)
{
scounter[s[i]-'a']++;
if(i<p_len-1) continue;//窗口还未达到p的长度
if(pcounter == scounter) res.push_back(l);//l = i-p_len+1
//在s_cnt中每次增加一个新字母,去除一个旧字母
scounter[s[l]-'a']--;//窗口移动
l++;
}
return res;
}
};
乘积小于k的数组
给定一个正整数数组 nums和整数 k 。
请找出该数组内乘积小于 k 的连续的子数组的个数。
输入: nums = [10,5,2,6], k = 100
输出: 8
解释: 8个乘积小于100的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于100的子数组。
class Solution {
public:
int numSubarrayProductLessThanK(vector<int>& nums, int k) {
if(k==0 || k==1) return 0;
int n = nums.size();
int l=0,r=0;
int s=1;
int res=0;
//超时
/*for(l=0;ln-1) break;
s*=nums[r] ;
if(s
while(r<n){
s *= nums[r++];
while(s >= k){
s /= nums[l++];
}
res += r-l;
}
return res;
}
};
岛屿问题详解
基本框架代码 dfs
void dfs(int[][] grid, int r, int c) {
// 判断 base case
if (!inArea(grid, r, c)) {
return;
}
// 如果这个格子不是岛屿,直接返回
if (grid[r][c] != 1) {
return;
}
grid[r][c] = 2; // 将格子标记为「已遍历过」
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}
作者:nettee
链接:https://leetcode-cn.com/problems/number-of-islands/solution/dao-yu-lei-wen-ti-de-tong-yong-jie-fa-dfs-bian-li-/
来源:力扣(LeetCode)
岛屿数量
题目描述:
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外,你可以假设该网格的四条边均被水包围。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/number-of-islands
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
class Solution {
public int numIslands(char[][] grid) {
int r = grid.length;
int c = grid[0].length;
int res=0;
for(int i=0;i<r;i++){
for(int j=0;j<c;j++){
if(grid[i][j] == '1'){
dfs(grid,i,j);
res++;
}
}
}
return res;
}
public void dfs(char[][] grid,int r,int c){
//边界
if(r<0 || r>= grid.length || c<0 || c>= grid[0].length
|| grid[r][c] != '1'){
return;
}
//标记访问过的岛屿
grid[r][c]='2';
dfs(grid,r+1,c);
dfs(grid,r-1,c);
dfs(grid,r,c+1);
dfs(grid,r,c-1);
}
}
岛屿周长
示例 2:
输入:grid = [[1]]
输出:4
class Solution {
public int islandPerimeter(int[][] grid) {
if(grid==null || grid.length==0){
return 0;
}
int res=0;
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
/*//1.简单的做法
if(grid[i][j]==1){
res+=4;
//检查左上方有无岛屿,有就-2
if(i>0 && grid[i-1][j] == 1){
res -= 2;
}
if(j>0 && grid[i][j-1] == 1){
res-=2;
}
}*/
//2.用dfs
if(grid[i][j] == 1){
res += dfs(grid,i,j);
}
}
}
return res;
}
public int dfs(int[][] grid,int r, int c){
// 边界
if(r<0 || c<0 || r>= grid.length || c>=grid[0].length){
return 1;
}
// 遇到海洋
if(grid[r][c] == 0){
return 1;
}
// 遍历过的岛屿
if(grid[r][c] != 1){
return 0;
}
grid[r][c] = 2;//标记遍历过的
return dfs(grid,r-1,c)+dfs(grid,r+1,c)+dfs(grid,r,c+1)+dfs(grid,r,c-1);
}
}
岛屿面积
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int r = grid.length;
int c = grid[0].length;
int res=0;
for(int i=0;i<r;i++){
for(int j=0;j<c;j++){
if(grid[i][j]==1){
int area=dfs(grid,i,j);
res = Math.max(res,area);
}
}
}
return res;
}
public int dfs(int[][] grid,int r,int c){
//判断越界
if(r<0 || c<0 || r>=grid.length || c>=grid[0].length || grid[r][c] != 1){
return 0;
}
//边界访问过的岛屿
grid[r][c] = 2;
/*
int count = 1;
count += dfs(grid, i+1, j);
count += dfs(grid, i-1, j);
count += dfs(grid, i, j+1);
count += dfs(grid, i, j-1);
return count;
*/
return 1+dfs(grid,r+1,c)+dfs(grid,r-1,c)+dfs(grid,r,c+1)+dfs(grid,r,c-1);
}
}
图的问题 省份数量(dfs)
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
class Solution {
public int findCircleNum(int[][] isConnected) {
if(isConnected == null || isConnected.length==0){
return 0;
}
//用来标记访问数组
boolean[] visited = new boolean[isConnected.length];
int res=0;
for(int i=0;i<isConnected.length;i++){
// 若当前顶点 i 未被访问,说明又是一个新的连通域,
if(!visited[i]){
res++;
dfs(isConnected,i,visited);
}
}
return res;
}
private void dfs(int[][] isConnected, int i, boolean[] visited){
// 标记访问过的数组
visited[i] = true;
// 遍历与顶点 i 相邻的顶点(使用 visited 数组防止重复访问)
for(int j=0;j<isConnected.length;j++){
if(isConnected[i][j]==1 && !visited[j]){
dfs(isConnected,j,visited);
}
}
}
}
二叉树的遍历
先/中/后序遍历
c++代码模板:
中序遍历:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
vec.push_back(cur->val); // 中
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
traversal(root, result);
return result;
}
};
java代码:
前序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
traversal(root,res);
return res;
}
public void traversal(TreeNode cur,List<Integer> list){
if(cur==null) {
return;
}
list.add(cur.val);
traversal(cur.left,list);
traversal(cur.right,list);
}
}
层序遍历
队列先进先出,符合一层一层遍历的逻辑
栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
c++ 代码模板
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
if(root != NULL) q.push(root);
vector<vector<int>> res;
while(!q.empty()){
int size = q.size();
vector<int> vec;
while(size-- > 0){
TreeNode* node = q.front();//取队首
q.pop();//出队列
vec.push_back(node->val);//将队首值存入vec数组
if(node->left != NULL) q.push(node->left);
if(node->right != NULL) q.push(node->right);
}
res.push_back(vec);
}
return res;
}
};
二叉树最大深度
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
class Solution {
public:
/**
*
* @param root TreeNode类
* @return int整型
*/
int maxDepth(TreeNode* root) {
// write code here
/*解法一:层序遍历
queue q;
if(root!=NULL) q.push(root);
int cnt=0;
while(!q.empty()){
int size = q.size();
cnt++;
while(size--){
TreeNode* node=q.front();
q.pop();
if(node->left!=NULL) q.push(node->left);
if(node->right!=NULL) q.push(node->right);
}
}
return cnt;*/
//递归写法:
if(root == NULL) return 0;
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
};
合并二叉树
已知两颗二叉树,将它们合并成一颗二叉树。合并规则是:都存在的结点,就将结点值加起来,否则空的位置就由另一个树的结点来代替。
输入: {1,3,2,5},{2,1,3,#,4,#,7}
返回值: {3,4,5,5,4,#,7}
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
// write code here
if(t1!=NULL && t2!=NULL){
t2->val +=t1->val;
t2->left = mergeTrees(t1->left,t2->left);
t2->right = mergeTrees(t1->right,t2->right);
}
return t2 == NULL ? t1 : t2;
}
二叉树的镜像
操作给定的二叉树,将其变换为源二叉树的镜像。 数据范围:二叉树的节点数 0≤n≤10000 \le n \le 10000≤n≤1000
, 二叉树每个节点的值 0≤val≤10000\le val \le 1000 0≤val≤1000
要求: 空间复杂度
O(n)O(n)O(n) 。
本题也有原地操作,即空间复杂度 O(1)O(1)O(1) 的解法,时间复杂度 O(n)O(n)O(n)
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pRoot TreeNode类
* @return TreeNode类
*/
TreeNode* Mirror(TreeNode* pRoot) {
// write code here
if(!pRoot)return pRoot;
queue<TreeNode*>q;
q.push(pRoot);
while(!q.empty()){
TreeNode* p = q.front();
q.pop();
TreeNode* temp = p->left;
p->left = p->right;
p->right = temp;
if(p->left)q.push(p->left);
if(p->right)q.push(p->right);
}
return pRoot;
}
};
判断二叉搜索树
二叉搜索树的定义: 二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根节点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值; (3)左、右子树也分别为二叉搜索树
1、中序遍历二叉树,判断得到的结果是否是升序排列
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
bool isValidBST(TreeNode* root) {
// write code here
if(root==NULL) return true;
vector<int> arr;
midddle(root, arr);
for(int i=0;i<arr.size()-1;i++){
if(arr[i]>arr[i+1]){
return false;
}
}
return true;
}
//中序遍历 判断数组是否升序
void midddle(TreeNode* root,vector<int> &vec){
if(root == NULL) return;
midddle(root->left,vec);
vec.push_back(root->val);
midddle(root->right,vec);
}
};
2、递归
step 1:首先递归到最左,初始化maxLeft与pre。
step 2:然后往后遍历整棵树,依次连接pre与当前节点,并更新pre。
step 3:左子树如果不是二叉搜索树返回false。
step 4:判断当前节点是不是小于前置节点,更新前置节点。
step 5:最后由右子树的后面节点决定。
class Solution {
public:
long pre = INT_MIN;
//中序遍历
bool isValidBST(TreeNode* root) {
if(root == NULL)
return true;
//先进入左子树
if(!isValidBST(root->left))
return false;
if(root->val <= pre)
return false;
//更新最值
pre = root->val;
//再进入右子树
if(!isValidBST(root->right))
return false;
return true;
}
};
判断完全二叉树
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
bool isCompleteTree(TreeNode* root) {
// write code here
if(root==NULL) return true;
queue<TreeNode*> q;
q.push(root);
bool flag = false;//这个flag用来作为是否是一棵完全二叉树的标记
while(!q.empty()){
int size = q.size();
while(size--){
TreeNode* node = q.front();
q.pop();
//这里如果当前结点为空,那么说明后续不应该再出现不为空的值
//就把flag置为真,表示这是一个完全二叉树
if(node==NULL) flag = true;
else{
//这里出现了不为空的结点,但是flag又表示一棵完全二叉树,故出现矛盾点,返回错误。
if(flag) return false;
q.push(node->left);
q.push(node->right);
}
}
}
return true;
}
};
判断是否是平衡二叉树
题目:
输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。
在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树
平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
class Solution {
public:
bool IsBalanced_Solution(TreeNode* pRoot) {
if(pRoot==NULL) return true;
int l = deep(pRoot->left);
int r = deep(pRoot->right);
// 高度差大于1就不是平衡二叉树
if(abs(l-r)>1) return false;
//递归判断左右子树是否平衡
return IsBalanced_Solution(pRoot->left)&&IsBalanced_Solution(pRoot->right);
}
//计算二叉树书的深度
int deep(TreeNode *root){
if(root==NULL) return 0;
return max(deep(root->left),deep(root->right))+1;
}
};
在二叉树中找到两个节点的最近公共祖先
1、递归
step 1:如果o1和o2中的任一个和root匹配,那么root就是最近公共祖先。
step 2:如果都不匹配,则分别递归左、右子树。
step 3:如果有一个节点出现在左子树,并且另一个节点出现在右子树,则root就是最近公共祖先.
step 4:如果两个节点都出现在左子树,则说明最低公共祖先在左子树中,否则在右子树。
step 5:继续递归左、右子树,直到遇到step1或者step3的情况。
class Solution {
public:
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
//该子树没找到,返回-1
if(root == NULL)
return -1;
//该节点是其中某一个节点
if(root->val == o1 || root->val == o2)
return root->val;
//左子树寻找公共祖先
int left = lowestCommonAncestor(root->left, o1, o2);
//右子树寻找公共祖先
int right = lowestCommonAncestor(root->right, o1, o2);
//左子树为没找到,则在右子树中
if(left == -1)
return right;
//右子树没找到,则在左子树中
if(right == -1)
return left;
//否则是当前节点
return root->val;
}
};
2、求包含该节点的路径
step 1:利用dfs求得根节点到两个目标节点的路径:每次选择二叉树的一棵子树往下找,同时路径数组增加这个遍历的节点值。
step 2:一旦遍历到了叶子节点也没有,则回溯到父节点,寻找其他路径,回溯时要去掉数组中刚刚加入的元素。
step 3:然后遍历两条路径数组,依次比较元素值。
step 4:找到两条路径第一个不相同的节点即是最近公共祖先
class Solution {
public:
//记录是否找到到o的路径
bool flag = false;
//求得根节点到目标节点的路径
void dfs(TreeNode* root, vector<int>& path, int o){
if(flag || root == NULL)
return;
path.push_back(root->val);
//节点值都不同,可以直接用值比较
if(root->val == o){
flag = true;
return;
}
//dfs遍历查找
dfs(root->left, path, o);
dfs(root->right, path, o);
//找到
if(flag)
return;
//该子树没有,回溯
path.pop_back();
}
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
vector<int> path1, path2;
//求根节点到两个节点的路径
dfs(root, path1, o1);
//重置flag,查找下一个
flag = false;
dfs(root, path2, o2);
int res;
//比较两个路径,找到第一个不同的点
for(int i = 0; i < path1.size() && i < path2.size(); i++){
if(path1[i] == path2[i])
//最后一个相同的节点就是最近公共祖先
res = path1[i];
else
break;
}
return res;
}
};
字符串题目练习
最长前缀
题目:
给定一个二叉树,确定他是否是一个完全二叉树。
完全二叉树的定义:若二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大个数,第 h 层所有的叶子结点都连续集中在最左边,这就是完全二叉树。(第 h 层可能包含 [1~2h] 个节点)
输入:
{1,2,3,4,5,6}
返回值:
true
输入:
{1,2,3,4,5,#,6}
返回值:
false
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
int n = strs.size();//字符数组的长度
int j = strs[0].size();//第一个子串的长度
string res = strs[0];//以第一个子串为基准 判断
int flag = 1;
if(n==1) return res;
while(flag==1 && j>=0){
for(int i=0;i<n;i++){
if(strs[i].find(res)!=0){//有一个不匹配就减字符重新匹配
break;
}
if(i==n-1 && strs[i].find(res) == 0){//所有的都匹配成功直接找到正确答案
flag=0;
}
}
if(flag){
res = res.erase(j--);//删除最后一位字符后再比较
}
}
if(flag == 1) res = "";
return res;
}
};
字符串排列查找 (用滑动窗口做)
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。
换句话说,s1 的排列之一是 s2 的 子串 。
示例:
输入:s1 = “ab” s2 = “eidbaooo”
输出:true
解释:s2 包含 s1 的排列之一 (“ba”).
class Solution {
public:
bool checkInclusion(string s1, string s2) {
//滑动窗口解法
// 利用长度为26的数组记录字母出现的频次 就可用来判断字母相同排列不同的组合
vector<int> s1cnt(26,0);
vector<int> s2cnt(26,0);
for(int i=0;i<s1.size();i++){
s1cnt[s1[i]-'a']++;
}
for(int i=0;i<s2.size();i++){
s2cnt[s2[i]-'a']++;
if(i<s1.size()-1) continue;//小于窗口大小 继续移动
if(s1cnt == s2cnt) return true;//找到一个直接返回true
s2cnt[s2[i-s1.size()+1]-'a']--;//没找到继续滑动窗口
}
return false;
}
};
大数的乘法(用字符串表示结果)
参考博客 大数相乘
关键:arr[i+j] += a[i]a[j]
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
num1 和 num2 的长度小于110。
num1 和 num2 只包含数字 0-9。
num1 和 num2 均不以零开头,除非是数字 0 本身。
不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。
string multiply(string num1, string num2) {
string res="";
vector<int> c(num1.size() + num2.size() + 1,0); //输出结果最大为a.size()+b.size()+1,其中加1考虑的是进位
for(int i=0;i<num1.size();i++){
for(int j=0;j<num2.size();j++){
int ai = num1[num1.size()-1-i]-'0';//最后一位开始 最低位
int bj = num2[num2.size()-1-j]-'0';
c[i+j] = c[i+j]+ai*bj;
}
}
//考虑进位
for(int i=0;i<c.size();i++){
if(c[i]>=10){
c[i+1] += c[i]/10;
c[i] %= 10;
}
}
//去掉高位的0
for(int i=c.size()-1;i>0;i--){//i>0 因为有可能乘积为0
if(c[i]==0 && c.size()!=1) c.pop_back();
else break;
}
//转化为字符 反向
for(int i=c.size()-1;i>=0;i--){
res += c[i]+'0';//转化为字符
}
return res;
}
大数加法
题目:
以字符串的形式读入两个数字,编写一个函数计算它们的和,以字符串形式返回。
#include翻转字符串
给你一个字符串 s ,逐个翻转字符串中的所有 单词 。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
请你返回一个翻转 s 中单词顺序并用单个空格相连的字符串。
说明:
输入字符串 s 可以在前面、后面或者单词间包含多余的空格。
翻转后单词间应当仅用一个空格分隔。
翻转后的字符串中不应包含额外的空格。
来源:力扣(LeetCode)
输入:s = " hello world "
输出:“world hello”
解释:输入字符串可以在前面或者后面包含多余的空格,但是翻转后的字符不能包括。
我的做法:
class Solution {
public:
string reverseWords(string s) {
// 先不要空格翻转
string res="";
for(int i=0;i<s.size();i++){
string temp="";//临时变量存每个单词
int j;
if(s[i] == ' ') continue;//空格就不管
if(s[i]!=' '){
j=i;
while(s[j]!=' ' && j<s.size()){//处理每个单词
temp+=s[j];
j++;
}
i=j-1;
res = ' '+temp+res;//将单词前插法插入res
}
}
res=res.erase(0,1);//处理首字符多余空格
return res;
}
};
官方题解:
class Solution {
public:
string reverseWords(string s) {
// 反转整个字符串
reverse(s.begin(), s.end());
int n = s.size();
int idx = 0;
for (int start = 0; start < n; ++start) {
if (s[start] != ' ') {
// 填一个空白字符然后将idx移动到下一个单词的开头位置
if (idx != 0) s[idx++] = ' ';
// 循环遍历至单词的末尾
int end = start;
while (end < n && s[end] != ' ') s[idx++] = s[end++];
// 反转整个单词
reverse(s.begin() + idx - (end - start), s.begin() + idx);
// 更新start,去找下一个单词
start = end;
}
}
s.erase(s.begin() + idx, s.end());
return s;
}
};
最长回文串
对于长度为n的一个字符串A(仅包含数字,大小写英文字母),请设计一个高效算法,计算其中最长回文子串的长度。
 具体做法:
具体做法:
step 1:遍历字符串每个字符。
step 2:以每次遍历到的字符为中心(分奇数长度和偶数长度两种情况),不断向两边扩展。
step 3:如果两边都是相同的就是回文,不断扩大到最大长度即是以这个字符(或偶数两个)为中心的最长回文子串。
step 4:我们比较完每个字符为中心的最长回文子串,取最大值即可。
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* @param A string字符串
* @return int整型
*/
每个中心点开始扩展
int fun(string& str,int l,int r){
while(l>=0 && r<str.length() && str[l]==str[r]){
l--;
r++;
}
return r-l-1;
}
int getLongestPalindrome(string A) {
// write code here
int res = 1;
if(A.length()<=1) return A.length();
//以每个点为中心,向外扩散
for(int i=0;i<A.length()-1;i++){
//分奇数长度和偶数长度向两边扩展
res = max(res,max(fun(A,i,i),fun(A,i,i+1)));
}
return res;
}
};
简化路径
用到stringstream 字符流方法
stringstream详解
//还不懂
class Solution {
public:
string simplifyPath(string path) {
// stringstream 用于字符串的输入输出 通常是用来做数据转换
stringstream istr(path);//
vector<string> strs;
string res="",tmp="";
while(getline(istr,tmp,'/')){
if(tmp=="" || tmp==".") continue;
else if(tmp == ".." &&!strs.empty()) strs.pop_back();
else if(tmp != "..") strs.push_back(tmp);
}
for(string str:strs) res += "/" +str;
if(res.empty()) return "/";
return res;
}
};
复原IP地址
startIndex记录下一层起始位置
pointNum记录添加‘.’的数量
终止条件为:分割点数量为3,说明字符串分成了4段了。
然后验证一下第四段是否合法,如果合法就加入到结果集里。
在循环中判断区间内的字符串是否合法,合法就加上分割点,不合法就结束本层循环剪枝。
递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符.),同时记录分割符的数量pointNum 要 +1。
回溯时,将刚刚加入的分隔符. 删除 用s.erase(),pointNum-1。
再有一个判断IP是否合法的函数
class Solution {
public:
vector<string> restoreIpAddresses(string s) {
int len = s.size();
vector<string> res;
res.clear();
if(len<4 || len>12) return res;//剪枝
backTrack(res,s,0,0);
return res;
}
//回溯法
void backTrack(vector<string> &res,string &s,int startIndex,int pointNum){
if(pointNum == 3) {//点为3 终止
if(isValid(s,startIndex,s.size()-1)){//判断第4段是否合法
res.push_back(s);
}
return;
}
for(int i=startIndex;i<s.size();i++){
if(isValid(s,startIndex,i)){//判断[index,i]区间是否合法
s.insert(s.begin()+i+1,'.');//在第i个后面插入‘.’
pointNum++;//点数增加
backTrack(res,s,i+2,pointNum);//插入逗点之后下一个子串的起始位置为i+2
pointNum--;//回溯
s.erase(s.begin()+i+1);//回溯删掉前一个'.'
}
else break;//剪枝
}
}
//判断字符串在l到r区间是否合法
bool isValid(const string& s,int l,int r){
if(l>r) return false;
if(s[l] == '0' && l != r) return false;//先导0不合法
else{
string temp;
for(int i=l;i<=r;i++) temp.push_back(s[i]);
int b;
stringstream ss;
ss<<temp;
ss>>b;
if(b<0||b>255) return false;
//字符串转数字
// int temp=0;
// for(int i=l;i<=r;i++){
// if(s[i]>'9' || s[i]<'0'){
// return false;
// }
// temp = temp*10 + (s[i]-'0');
// if(temp>255) return false;
// }
}
return true;
}
};
并查集学习
添加链接描述
合并有序数组
题目:
给出一个有序的整数数组 A 和有序的整数数组 B ,请将数组 B 合并到数组 A 中,变成一个有序的升序数组
数据范围: 0≤n,m≤1000 \le n,m \le 1000≤n,m≤100,∣Ai∣<=100|A_i| <=100∣Ai∣<=100, ∣Bi∣<=100|B_i| <= 100∣Bi∣<=100
输入:
[4,5,6],[1,2,3]
返回值:
[1,2,3,4,5,6]
注意:
1.保证 A 数组有足够的空间存放 B 数组的元素, A 和 B 中初始的元素数目分别为 m 和 n,A的数组空间大小为 m+n
void merge(int A[], int m, int B[], int n) {
int j=n-1,i=m-1;
int p = n+m-1;
while(i>=0 && j>=0){
A[p--] = A[i] > B[j] ? A[i--] : B[j--];
}
while(j>=0) A[p--] = B[j--];
//return A;
for(int k=0;k<m+n;k++) cout<<A[k]<<" ";
}
合并区间
输入:
[[10,30],[20,60],[80,100],[150,180]]
返回值:
[[10,60],[80,100],[150,180]]
/**
* Definition for an interval.
* struct Interval {
* int start;
* int end;
* Interval() : start(0), end(0) {}
* Interval(int s, int e) : start(s), end(e) {}
* };
*/
class Solution {
public:
static bool compare(Interval &a, Interval &b){
return a.start<b.start;
};
vector<Interval> merge(vector<Interval> &intervals) {
vector<Interval> res;
//特殊情况
if(intervals.size() == 0)
return res;
//按start 排序
sort(intervals.begin(),intervals.end(),compare);
//将第一个放入
res.push_back(intervals[0]);
for(int i=1;i<intervals.size();i++){
if(intervals[i].start<=res.back().end){
//更新最后一个的end
res.back().end = max(res.back().end, intervals[i].end);
}else{
//没有重叠 直接加入
res.push_back(intervals[i]);
}
}
return res;
}
};
最长公共子序列
给定两个字符串str1和str2,输出两个字符串的最长公共子序列。如果最长公共子序列为空,则返回"-1"。目前给出的数据,仅仅会存在一个最长的公共子序列
输入:
“1A2C3D4B56”,“B1D23A456A”
返回值:
“123456”
class Solution {
public:
/**
* longest common subsequence
* @param s1 string字符串 the string
* @param s2 string字符串 the string
* @return string字符串
*/
string LCS(string s1, string s2) {
// write code here
if(s1=="" || s2 =="") return "-1";
int dp[s1.size()+1][s2.size()+1];
//初始化
for(int i=0;i<=s1.length();i++) dp[i][0] = 0;
for(int j=0;j<=s2.length();j++) dp[0][j] = 0;
//构造dp
for(int i=1;i<=s1.length();i++){
for(int j=1;j<=s2.length();j++){
if(s1[i-1]==s2[j-1]){
dp[i][j] = dp[i-1][j-1]+1;
}else{
dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
}
}
}
string res="";
int i=s1.size(),j=s2.size();
while(dp[i][j]>=1){
if(s1[i-1]==s2[j-1]){
res+=s1[i-1];
i--;
j--;
}else if(dp[i-1][j]>=dp[i][j-1]) {
i--;
} else{
j--;
}
}
reverse(res.begin(),res.end());
return res.empty() ? "-1" : res;
}
};