保姆级别带你手撕红黑树BRTree
目录
二、从头介绍
三、引出红黑树
四、红黑树性质
五、红黑树的一些推论
六、手撕BRTree
6.1、红黑树结点的结构体
6.2、红黑树结构体
6.3、左旋操作
6.4、右旋操作
6.5、插入新结点操作
6.6、插入新结点后调整
6.7、删除结点
6.7.1、查找某个结点
6.7.2、找以某结点为根的那棵树的最小/大值结点
6.7.3、找某结点的中序遍历的后继结点
6.7.4、如何删除结点
6.8、删除结点后进行调整
6.9 测试
七、总结
本文是自己在学习过程中，记录下的一些总结，以便日后复习，同时分享出来，方便与更多人学习交流，共同进步。（不要看篇幅长就吓住，其实不难，只是我画了很多图，做了很详细的解释）鄙人水平有限，若有误，请不吝赐教。
二、从头介绍
红黑树树是一种二叉树，比较常用的数据结构，如果对二叉树不是很熟悉或者有遗忘的朋友，可以看看我之前做的笔记。
第一篇介绍二叉树的基础知识：数据结构与算法 树_振予的博客-CSDN博客
第二篇介绍二叉搜索树和二叉平衡树树：数据结构与算法 查找_振予的博客-CSDN博客
三、引出红黑树
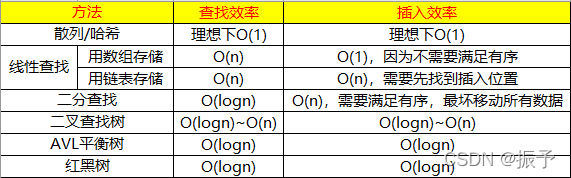
每当我们打开电脑查找一个文档、在教务系统输入我们的用户名、上网购物搜索时，都会用到查找这个功能，查找的效率直接关系到用户体验的舒适度。不同的应用场景和不同量级别的数据采取的查找策略也不同。下面，从简单的说起：（假如我们的数据量为n）
哈希/散列查找，根据key值计算value，理想情况下效率为O(1)。不过得构造一个好的哈希函数。
线性查找，挨个比对，效率最低，时间复杂度为O(n)。
二分查找，每次能排除一半的数据，前提是有序，时间复杂度为O(logn)。
二叉查找树，平均效率和二分查找一样，但是，当二叉查找树结构成为二叉链（即，全是右孩子或左孩子），又退化成线性查找O(n)。
AVL平衡树，查找效率高，时间复杂度O(logn)。
红黑树，也是一种比较平衡的二叉树，查找时间复杂度O(logn)。
前面总结了查找效率，同时，插入一个数据也需要不能太慢。对于对于线性查找，在线性表中插入一个数据，最坏情况下需要移动所有数据，二分查找也一样。二叉查找树插入效率最好情况为O(logn)，最坏会退化到O(n)。因此出现了AVL平衡树，它的所有结点的左右子树高度差不超过1，因此对于查找来说，是极好的，但是当有频繁插入数据操作时，可能每一次插入都需要进行调整，效率就又低下来了，于是有红黑树就好办了，红黑树的平衡要求没有AVL严格，但是又保证了查找的效率，综合两种因素，因此应用场景也比较多（Linux进程调度CFS、Nginx Timer事件管理、Epoll事件块的管理）。
四、红黑树性质
1、每个结点是红色的或者黑色的
2、根结点是黑色的
3、规定每个叶子结点NIL是黑色的
4、每个红色结点的子结点都是黑色的
5、对于每个结点，该结点到其所有子孙结点的所有路径上包含相同数目的黑结点（相同黑高）
******（提炼出三条非常非常重要的结论：根为黑、红子为黑、黑高相同）******
（后面堆红黑树进行插入，是否需要修复就是根据这三个性质）
一颗红黑树（隐藏了叶子结点NIL）
五、红黑树的一些推论
我们可以由前面的几条性质得到一些推论如下：
1、红黑树可以没有红色结点
2、树中一定有黑色存在，即使root==NIL，也可看做黑色
3、红色结点的父结点一定存在且为黑色
4、黑色结点可以连续存在
5、最长路径至多是最短路径的两倍
6、任意一条路径上不可能存在两个连续的红色结点（红色结点没有红色父亲和红色孩子）
六、手撕BRTree
红黑树能便于我们快速的查找元素，我们在插入一个元素之后或者删除一个元素之后，需要保持红黑树的性质，因此插入后者删除后可能失衡，就得进行调整，红黑树的难点也在这里，下面一一分析。
6.1、红黑树结点的结构体
一个结点有颜色、左孩子、右孩子、父结点、值域和其他操作。如下：
#include
#include
#include
#define RED 1
#define BLACK 2
typedef int KEY_TYPE; // 值域的类型根据实际情况而定
typedef struct _rbtree_node {
unsigned char color;
struct _rbtree_node *right;
struct _rbtree_node *left;
struct _rbtree_node *parent;
KEY_TYPE key;
void *value;
} rbtree_node;
int main()
{
return 0;
} 6.2、红黑树结构体
typedef struct struct_rbtree{
rbtree_node *root; // 根结点
rbtree_node *nil; // 通用叶子结点的孩子，哨兵
}rbtree;这里解释一下哨兵：为了便于处理红黑树代码中的边界条件，使用一个哨兵来代表NIL。对于一颗红黑树T，哨兵T.nil是一个与普通结点具有相同属性的对象，它的color为BLACK，其他属性可以设为任意值，如下图，所有指向NIL的指针可以用哨兵T.nil的指针替换。
6.3、左旋操作
结点x和y不能为T.nil，左旋后，x成为y的左孩子，y的左孩子成为x的右孩子。看图写代码：
（注意，每次旋转时，传的参数是离根结点近的那个结点）
void rbtree_left_rotate(rbtree *T, rbtree_node *x){ // 将T树的x结点左旋
rbtree_node *y = x->right; // 结点的右孩子
// 1、x右孩子 <==> y左孩子
x->right = y->left; // x结点的右孩子指向y结点的左孩子
if(y->left != T->nil){ // 如果y的左孩子不空，则左孩子的父节点指向x
y->left->parent = x;
}
// 2、x右孩子y <==> x父节点互相指
y->parent = x->parent;
if(x->parent == T->nil){
T->root = y;
} else if(x == x->parent->left){
x->parent->left = y;
} else {
x->parent->right = y;
}
// 3、x <==> y左孩子
y->left = x;
x->parent = y;
}6.4、右旋操作
结点x和y不能为T.nil，左旋后，y成为x的右孩子，x的右孩子成为y的左孩子。看图写代码：
（注意，每次旋转时，传的参数是离根结点近的那个结点）
void rbtree_right_rotate(rbtree *T, rbtree_node *y){ // 将T树的y结点右旋
rbtree_node *x = y->left; // 结点的左孩子
// 1、y左孩子 <==> x右孩子
y->left = x->right; // x结点的右孩子指向y结点的左孩子
if(x->right != T->nil){ // 如果y的左孩子不空，则左孩子的父结点指向x
x->right->parent = y;
}
// 2、y左孩子 <==> y父结点互相指
x->parent = y->parent;
if(y->parent == T->nil){
T->root = x;
} else if(y == y->parent->right){
y->parent->right = x;
} else {
y->parent->left = x;
}
// 3、y <==> x右孩子
x->right = y;
y->parent = x;
}6.5、插入新结点操作
先来来复习一下三条最重要的性质：根为黑、红子为黑、黑高相同。
插入结点时，先找到应该插入的位置，按照一颗普通的二叉搜索树，加入插入结点为z，那么就不断遍历T树，从树根开始，如果z->key小于当前遍历的结点的值域，则往左继续找，否则往右，直到到达叶子结点。插入后需要将z结点的颜色赋为红色（因为，如果赋为黑色会马上破坏黑高这条性质，如果赋为红色，有可能不会破坏三条重要的性质，就不用修复，大大提高效率），下面是插入的代码：
void rbtree_insert(rbtree *T, rbtree_node *z){ // 在T树中插入结点z
rbtree_node *x = T->root;
rbtree_node *y = T->nil; // y是x的父结点
while(x != T->nil){
y = x;
if(z->key < x->key){ // 新结点值域比当前结点值域小往左子树找
x = x->left;
} else if(z->key > x->key){ // 新结点值域比当前结点值域小往左子树找
x = x->right;
} else { // 相等时，不同场景处理不同
return ;
}
}
z->parent = y; // z的父结点指向y
if(y == T->nil){ // 如果T是空树
T->root = z; // T的根结点则是z
} else if(z->key < y->key){ // 新结点插入到y的左孩子结点上
y->left = z;
} else{ // 新结点插入到y的右孩子结点上
y->right = z;
}
z->left = T->nil; // 叶子结点的左孩子赋值T->nil
z->right = T->nil; // 叶子结点的右孩子赋值T->nil
z->color = RED; // 将z结点颜色赋为红色
rbtree_insert_fixup(T, z); // 插入后可能需要调整，此函数在下面一小节
}6.6、插入新结点后调整
为了更好理解，我们做一些说明：
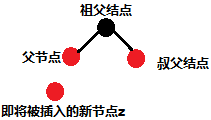
插入的新结点为z，其父结点的父结点叫祖父结点，其祖父结点的另一个孩子结点叫叔父结点：
插入删除修正一个大的原则:
可以通过染色直接解决修复问题则先染色，否则再考虑旋转，尽量把问题控制在局部进行。每次插入一个新结点，只有两种性质2（根结点是黑色的）和性质4（每个红色结点的子结点都是黑色的）可能被破坏。我们对所有的可能出现的情况和策略做分析：
1、父结点为空，即z是根结点，染黑即可；
2、插入到黑色结点上面，没有破坏性质2和4，不用修复；
3、插入到红色结点上面，需要修复，这里分两大类情况分析（每一类又可以分为新插入的结点z，其父结点是左孩子还是右孩子讨论）：
a、新插入的结点z有叔父结点且为红色；
这种情况，需要把父结点和叔父结点颜色变为黑色，祖父结点变为红色，即父辈结点的颜色与之前相反，然后z = 祖父结点，让其等价为新插入的结点，因为祖父结点变为红色可能会破坏了红黑树的性质，就这样一直回溯的修复，直到新等价的插入结点的父结点为黑色，或者直到回溯到根结点，最后把根重新变黑一下。
【1】、z结点的父结点是祖父结点的左孩子：
【2】、z结点的父结点是祖父结点的右孩子：
说明：情况a中，插入的新结点z是左孩子还是右孩子都没有区别，我们插入后就不会对z进行改动。虽然【1】和【2】好像没有区别，但是在写代码的时候，我们需要分区清插入的新结点是祖父结点的左孩子还是右孩子，便于判断叔父结点应在在哪边，当然也可以合并到一个判断语句中，只不过代码就很长，比较冗余了，不便阅读和更改。
b、新插入的结点没有叔父结点或者有叔父结点且为黑色；
这种情况，需要把新插入的结点z变为和其父结点成为一条线上，即如果父结点是祖父结点的左孩子，则z结点也得旋转到左边；如果是右孩子则z结点也得旋转到右边。然后让父结点与祖父结点颜色互换，再旋转祖父结点，这是父结点和祖父结点身份互换了，也达到了修复的目的。（左/右旋操作前面已经说过了，就不再细说）
【1】、父结点是祖父结点的左孩子：
444和555分别改变颜色，然后555结点右旋。
z结点先左旋，到三结点成一条线，然后500和555结点改变颜色，555结点再右旋。
【2】、父结点是祖父结点的右孩子：
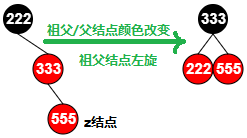
222和333结点改变颜色，然后222结点左旋。
z结点先甩到和父结点祖父结点一条线上，然后祖父结点变红，父结点变黑，再让祖父结点左旋。
不想看我说废话的可以跳过我下面用括号括起来的这些内容，直接跳到总结图哪那里！
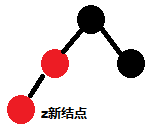
【【【不知道细心的朋友有没有发现，前面说了，b这种情况， 是新插入的结点没有叔父结点或者有叔父结点且为黑色，上面举的几种例子没有出现过叔父结点为黑色的。why? 想一想就能发现，其实不会在刚刚插入z结点就出现叔父结点为黑色的情况，如果有，就成了这样：
在z结点插入之前，就已经不满足红黑树的性质了。那么啥时候会出现z结点的叔父结点为黑色呢。还记得前面的a情况吗？a情况中，当改变父结点、叔父结点和祖父结点的颜色时，会把祖父结点更新为新的插入结点，因为祖父结点变为红色后，可能与他的父结点产生矛盾，这种时候就可能出现z结点的叔父结点为黑色，看下面：
ok，废话不多说，最后的总结，下面上一个图】】】
上代码：
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) { // 插入后修复，调整z结点
while (z->parent->color == RED) { // 当z结点的父节点是红色的，就需要一直调整
if (z->parent == z->parent->parent->left) { // z的父节点是z的祖父结点的左孩子
rbtree_node *uncle = z->parent->parent->right; // 祖父结点的右孩子 - 叔父结点
if (uncle->color == RED) { // 如果叔父是红色的，则改变祖父结点、其左右孩子结点、z的颜色
z->parent->color = BLACK;
uncle->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; // 更新z结点为其祖父结点
} else { // 如果叔父结点为黑色（包含了不存在的情况，即是T->nil时，其颜色也是黑色的）
if (z == z->parent->right) { // z为其父结点的右孩子。这时需要把三辈分结点调整到一条线上
z = z->parent; // 为了让左旋后，z还是孩子节点，提前将父节点赋为z
rbtree_left_rotate(T, z); // 左旋
}
z->parent->color = BLACK; // 将其父节点改为黑色
z->parent->parent->color = RED; // 其祖父结点改为红色
rbtree_right_rotate(T, z->parent->parent); // 祖父结点右旋
return ; // 这种情况调整完直接就修复完了
}
} else { // z的父节点是z的祖父结点的右孩子
rbtree_node *uncle = z->parent->parent->left; // 祖父结点的左孩子 - 叔父结点
if (uncle->color == RED) { // 如果叔父是红色的，则改变祖父结点、其左右孩子结点、z的颜色
z->parent->color = BLACK;
uncle->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; // 更新z结点为其祖父结点
} else { // 如果叔父结点为黑色（包含了不存在的情况，即是T->nil时，其颜色也是黑色的）
if (z == z->parent->left) { // z为其父结点的左孩子。这时需要把三辈分结点调整到一条线上
z = z->parent; // 为了让右旋后，z还是孩子节点，提前将父节点赋为z
rbtree_right_rotate(T, z); // 右旋
}
z->parent->color = BLACK; // 将其父节点改为黑色
z->parent->parent->color = RED; // 其祖父结点改为红色
rbtree_left_rotate(T, z->parent->parent); // 祖父结点左旋
return ; // 这种情况调整完直接就修复完了
}
}
}
T->root->color = BLACK; // 以防根结点被更新成其他结点，所以需要再次赋一下颜色
}代码说明：函数里有一个while循环，一直修复，直到修复完成或者到达树根。主要分成了两种情况，父结点是祖父结点的左孩子还是右孩子（这里分类和前面介绍分类不同）每种情况下，又分为叔父结点的不存在/存在颜色为黑、存在颜色为红两类。之所以代码这样写，因为可以先写父结点是祖父结点的左孩子，然后else里的代码直接赋值if里的代码，然后把left和right互换就行，节省时间。
6.7、删除结点
删除结点比插入插入结点稍微复杂，不过不要怕，如果上面的都已经理解了，那么鼓励一下自己吧：
首先要找到删除结点的位置，这个很简单，就是搜索要删除的结点，我们先来看看下面一些代码。因为后面会用到。
6.7.1、查找某个结点
rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) { // 根据关键字key查找结点
rbtree_node *node = T->root;
while (node != T->nil) {
if (key < node->key) { // 往左找
node = node->left;
} else if (key > node->key) { // 往右找
node = node->right;
} else { // 找到，返回该结点
return node;
}
}
return T->nil; // 没有找到
}6.7.2、找以某结点为根的那棵树的最小/大值结点
rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) { // 找以x为根的最左边的那个结点
while (x->left != T->nil) { // 只要不为空，就一直往左边找
x = x->left;
}
return x;
}
rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) { // 找以x为根的最左边的那个结点
while (x->right != T->nil) { // 只要不为空，就一直往右边找
x = x->right;
}
return x;
}6.7.3、找某结点的中序遍历的后继结点
比如这棵树，中序遍历结果为：2、3、4、6、7、9、13、15、17、18、20（是有序的）
如果某个结点有右孩子，则右孩子的最左边的那个结点（包括右孩子）就是它的后继结点，比如6的后继结点是7，3的后继结点是4。如果没有右孩子，则不断往上找，对应代码的while循环，因为我们中序遍历的时候，先不断递归到某个结点的左孩子，左子树全部遍历结束后，才到根结点，比如，13结点的后继结点是15，要把15结点的所有左子树遍历完才遍历15，那么我们找某个结点的后继结点时，需要递归找父结点的父结点，并且每次都是父结点的右孩子才行，如果最终返回的不是空，则找到了，否则，该结点是最后一个结点，它没有后继结点，比如20是最后一个结点，没有后继结点。
rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x) { // 找到z的后继结点
rbtree_node *y = x->parent;
if (x->right != T->nil) { // 找到比x结点的key大的最小的值的结点
return rbtree_mini(T, x->right);
}
while ((y != T->nil) && (x == y->right)) {
x = y;
y = y->parent;
}
return y;
}6.7.4、如何删除结点
先不讨论，删除结点会不会影响颜色的平衡，先按照二叉查找树来看看如何删除。分三种情况：
第一、该结点没有左右孩子，那么直接删除即可。
第二、有一个孩子，那么让孩子顶替该结点的位置即可。
第三、有两个孩子，需要找到该结点的后继结点，去顶替该结点。为了简便，我们可以先找到该结点的后继结点，然后让后继结点的值赋给该结点，这时就等于删除后继结点，不断递归，最终会递归到前面两种情况的某一种。
（这个思路是完全按照《算法导论》的伪代码，如果想要这本PDF可以在评论区留言）
好，下面看看代码如何写：（如果还是有点懵，请看代码后面的图）
rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) { // z是即将被被删除的结点
rbtree_node *y = T->nil; // y指向将要被删除的结点，初始为nil
rbtree_node *x = T->nil; // x指向将要被删除的结点的唯一儿子
// 如果z有一个孩子为空，那么可以直接删除z，先让y指向z
if ((z->left == T->nil) || (z->right == T->nil)) {
y = z;
} else { // 否则有两个孩子结点，那么需要找到z的后继结点
y = rbtree_successor(T, z); // 找到按照中序遍历结果中z的后继结点
}
// x为即将被删除结点y的孩子，以便后面让x顶替y的位置
if (y->left != T->nil) {
x = y->left;
} else if (y->right != T->nil) {
x = y->right;
}
x->parent = y->parent; // 让y的孩子指向y的父结点
if (y->parent == T->nil) { // y是根结点，删除y，它的孩子就是根结点了
T->root = x;
} else if (y == y->parent->left) { // x顶替y作为它父亲左孩子的位置
y->parent->left = x;
} else { // x顶替y作为它父亲右孩子的位置
y->parent->right = x;
}
if (y != z) { // 这个y是替代的结点，即是z的后继结点（因为z有左右孩子，所以需要找后继结点）
// 此时，把后继结点的值传给了z，改而去删除后继结点
z->key = y->key;
z->value = y->value;
}
if (y->color == BLACK) { // 如果被删除的结点的颜色是黑色，就需要调整一下，否则会影响黑高
rbtree_delete_fixup(T, x); // 然后传入被删除结点的孩子作为参数
}
return y; // 最后返回被删除的结点，释放它的空间
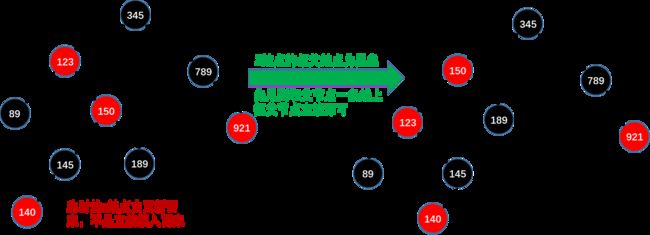
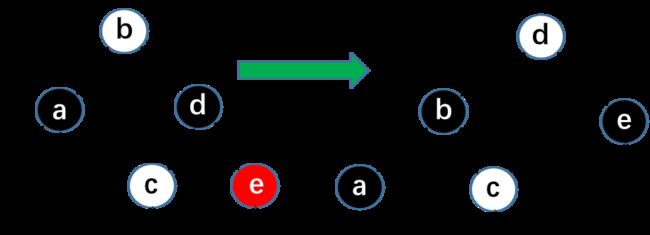
}我们把所有可能的情况用图画出来，如下：（别介意图，有亿点点丑）
第1、5情况，可以直接删除，第2、3、6、7删除后用其孩子顶替z的位置，第4、8情况，先找到后继结点，然后把后继结点的值传给z结点，再去删除后继结点y。注意，上面一排，z不是根结点，下面一排z是根结点，根结点的父结点用T->nil哨兵代替（红黑树种，根结点的父亲和叶子结点的孩子都用哨兵T->nil代替，而不是像二叉树的NULL这种）。然后，不会出现情况9，它的后继结点在上面，因为这种情况，z没有右孩子，而没有右孩子的时候，我们按照情况1、2或者5、6处理。这样就完美对照开头说的第一、第二、第三。
这里为什么要多用两个变量x、y？x是指向即将删除结点的孩子，让孩子替代被删除结点的位置，至于y，用以判断z == y？，如果不等，就是找的替补，如果相等就是直接删除，这两种情况的处理不一样，所以要两个变量。最后需要判断被删除结点y的颜色，如是黑色，我们还需要做调整。
6.8、删除结点后进行调整
能看到这里的朋友，都不简单哟！加油！
也许你会看了一些博客，发现他们的方式和这里不同，别怀疑，调整方式也有不同，但是最后能调整好，不破坏红黑树的性质都是ok的。这里完全按照《算法导论》的介绍，进行调整，一共分了两大类，第一大类就是x结点是红色的，这时只需要把其变黑，就可以弥补上因被删除结点而减少的黑高，第二大类，x结点本来就是黑色的，这就需要其兄弟结点帮忙了，这时就又分四种情况。
情况1：x的兄弟w是红色的。
改变w和x.parent结点的颜色，即w变黑色，x.parent变红色，然后左旋x.parent，然后就转为下面的某个情况了，如果w是黑色的，也会在下面的2、3、4某种情况中。
情况2：x的兄弟结点w是黑色的，而且w的两个子结点都是黑色的。
只需要把兄弟结点变红，就使得两边的黑高相同了，但是x.parent结点b的颜色不知道，如果为红色，就会跳出while循环，在最后会再给x重新赋为黑色。
情况3：x的兄弟结点w是黑色的，w的左孩子是红色的，右孩子是黑色的。
交换兄弟结点w和其左孩子的颜色，然后对兄弟结点w进行右旋，这时，兄弟结点w的左孩子就成了新的兄弟结点，然后就转成了情况4。
情况4：x的兄弟结点w是黑色的，右孩子是红色的。
将兄弟结点与其父结点颜色交换，再将兄弟结点的右孩子染黑，然后将父结点左旋，最后将x设为树根，就跳出了循环。
下面看代码如如何写：
void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {
while ((x != T->root) && (x->color == BLACK)) { // x不为树根且x的颜色为黑色时
if (x == x->parent->left) { // x是左孩子
rbtree_node *w = x->parent->right; // w是x的兄弟结点
if (w->color == RED) { // 情况1：兄弟结点w是红色的
w->color = BLACK;
x->parent->color = RED;
rbtree_left_rotate(T, x->parent);
w = x->parent->right; // 左旋后，更新兄弟结点w，进入情况2、3、4某一种
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) { // 情况2：黑色兄弟结点左右孩子全黑
w->color = RED;
x = x->parent;
} else {
if (w->right->color == BLACK) { // 情况3：黑色兄弟结点右孩子是黑色的
w->left->color = BLACK;
w->color = RED;
rbtree_right_rotate(T, w);
w = x->parent->right; // 右旋后，更新兄弟结点w，进入情况4
}
/* 下面是情况4（黑色兄弟结点w的右孩子是红色的）的操作 */
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
rbtree_left_rotate(T, x->parent);
x = T->root; // 将x设置为根，结束调整，退出while循环
}
} else { // x是右孩子。可以完全复制上面代码，然后left<->right互换
rbtree_node *w = x->parent->left;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_right_rotate(T, x->parent);
w = x->parent->left;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->left->color == BLACK) {
w->right->color = BLACK;
w->color = RED;
rbtree_left_rotate(T, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
rbtree_right_rotate(T, x->parent);
x = T->root;
}
}
}
x->color = BLACK; // 如果x的颜色不为红的，让x颜色变黑就弥补上被删除结点的缺失的黑高了
}6.9 测试
终，终，终于结束了，估计你也看累了，我写到这里手也废了，能不能给个赞呀，呜呜，qwq。
好了，还是要看看代码到底有没有bug，那么来测试一下下喽。
我们一共写了这些函数：
左旋、右旋、找x的最左子结点、找x的最右子节点、插入结点、插入后修复、找z的后继结点、删除结点、删除后修复、遍历树、查找某结点。
还有一个遍历树没有写，下面来吧：
void rbtree_traversal(rbtree *T, rbtree_node *node) { // 遍历
if (node != T->nil) {
rbtree_traversal(T, node->left); // 左子树
printf("key:%d, color:%d\n", node->key, node->color); // 输出key和颜色
rbtree_traversal(T, node->right); // 右子树
}
}下面是主函数，就没有把其他函数放进来了，你可以把上面的函数放到自己的主函数上面，完全可以跑起来的，我每个都测试成功了才放出来的。
int main() {
int keyArray[20] = {24, 25, 13, 35, 23, 26, 67, 47, 38, 98, 20, 19, 17, 49, 12, 21, 9, 18, 14, 15};
rbtree *T = (rbtree *)malloc(sizeof(rbtree)); // 定义一棵树
if (T == NULL) { // 申请空间失败
printf("malloc failed\n");
return -1;
}
/* 红黑树的哨兵（树根结点的父结点和叶子结点的孩子指向它） */
T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
T->nil->color = BLACK;
T->root = T->nil;
rbtree_node *node = T->nil;
int i = 0;
for (i = 0;i < 20;i ++) { // 插入结点
node = (rbtree_node*)malloc(sizeof(rbtree_node));
node->key = keyArray[i];
node->value = NULL;
rbtree_insert(T, node);
}
rbtree_traversal(T, T->root); // 遍历红黑树
printf("----------------------------------------\n");
for (i = 0;i < 20;i ++) { // 删除节点
rbtree_node *node = rbtree_search(T, keyArray[i]); // 先找到要删除key为keyArray[i]的结点
rbtree_node *cur = rbtree_delete(T, node); // 删除
free(cur); // 释放空间
rbtree_traversal(T, T->root); // 删除后遍历一下
printf("----------------------------------------\n");
}
}那么结果如何呢？
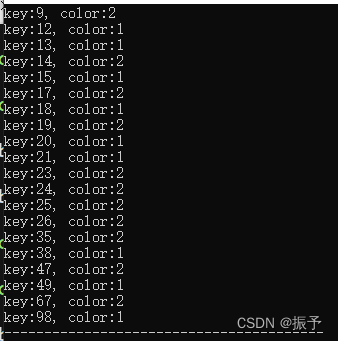
这是建立红黑树完成，输出整棵树。
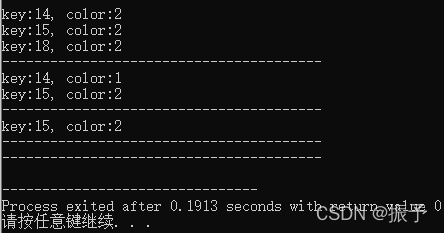
这时每删除一个结点就输出一下树，图中只展示了最后删除几个结点后输出树的情况，最后一个输出时树已经空了，只输出了一根虚线。
七、总结
前前后后主要从引入红黑树，到对红黑树的各种操作做了详细的介绍。红黑树用的地方很多，还需要进一步学习（我是说我自己，大佬请忽略）。由于篇幅长，难免有出错的地方，若有误，请评论区或私信留言。最后需要代码又不想一个一个的粘贴复制的，评论区留言。如果这篇文章对你有帮助，可以多多转发，评论，关注。感谢您的认可！