使用Java实现二叉树相关问题
使用Java实现二叉树相关问题
- 根据前序和中序遍历重建二叉树
- 根据已知二叉树求其前序遍历、中序遍历、后序遍历以及层次遍历
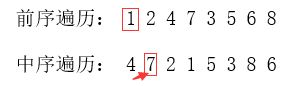
1. 题目：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。
分析：根据前序遍历和中序遍历很容易求得二叉树，并画出其图形，如下图所示。
前序遍历第一个值为根节点的值，可以依次对比中序遍历得到的数组中的值，当等于根节点时，中序遍历数组中根节点的左部分为左子树，右部分为右子树。其左右子树也采取同样的方式划分，直到该二叉树被重建。
- 前序遍历中第一个节点即根节点保持不动，依次对比中序遍历，分出左右子树。
![**[1,2,4,7,3,5,6,8]**](http://img.e-com-net.com/image/info8/4dc18531e87d4b0ea08eb03b10b46abc.jpg)
- 对左子树执行相同操作。
- 对右子树执行相同操作。
代码实现：
// 二叉树定义
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
@Override
public String toString() {
return "TreeNode [val=" + val + ", left=" + left + ", right=" + right
+ "]";
}
//重建二叉树代码
public static TreeNode reConstructBinaryTree(int[] pre, int[] in) {
//pre为前序遍历数组，in为中序遍历数组，加上其收尾下标值
TreeNode tree = binaryTreeRecursive(pre,0,pre.length-1,in,0,in.length-1);
return tree;
}
public static TreeNode binaryTreeRecursive(int[] pre, int preStart, int preEnd,
int[] in, int inStart, int inEnd) {
TreeNode treeNode = new TreeNode(pre[preStart]);
treeNode.left = null;
treeNode.right = null;
if (preStart == preEnd && inStart == inEnd) {
return treeNode;
}
int root = 0; //每次都找出根节点所在位置
for (root = inStart; root < in.length; root++) {
if (pre[preStart] == in[root]) {
break;
}
}
int leftLength = root - inStart;
int rightLength = inEnd - root;
if (leftLength>0) {
treeNode.left = binaryTreeRecursive(pre, preStart + 1, preStart + leftLength, in, inStart, root - 1);
}
if (rightLength>0) {
treeNode.right = binaryTreeRecursive(pre, preStart + leftLength + 1, preEnd, in, root + 1, inEnd);
}
return treeNode;
}
打印结果为：
TreeNode [val=1, left=TreeNode [val=2, left=TreeNode [val=4, left=null, right=TreeNode [val=7, left=null, right=null]], right=null], right=TreeNode [val=3, left=TreeNode [val=5, left=null, right=null], right=TreeNode [val=6, left=TreeNode [val=8, left=null, right=null], right=null]]]
2. 题目：根据已知二叉树求其前序遍历、中序遍历、后序遍历以及层次遍历。
分析：前序遍历、中序遍历和后序遍历比较简单，层次遍历需要借助队列实现。
代码实现如下：
private static List preResult = new ArrayList();
private static List inResult = new ArrayList();
private static List postResult = new ArrayList();
private static List levelResult = new ArrayList();
//main函数调用
//先序遍历
preTraverseBinTree(tree);
System.out.println("先序遍历为："+preResult.toString());
//中序遍历
inTraverseBinTree(tree);
System.out.println("中序遍历为："+inResult.toString());
//后序遍历
postTraverseBinTree(tree);
System.out.println("后序遍历为："+postResult.toString());
//层次遍历
levelTraverseBinTree(tree);
System.out.println("层次遍历为："+levelResult.toString());
//方法实现
//后序遍历
private static void postTraverseBinTree(TreeNode tree) {
if (tree == null) { //返回递归的上一级
return;
}
if (tree.left!=null) {
postTraverseBinTree(tree.left);
}
if (tree.right!=null) {
postTraverseBinTree(tree.right);
}
postResult.add(tree.val + "");
}
//层次遍历 借助队列
private static void levelTraverseBinTree(TreeNode tree) {
Queue queue = new LinkedList();
queue.add(tree);
while (!queue.isEmpty()) {
int count = queue.size();
List list=new ArrayList();
while (count>0) {
TreeNode temp = queue.peek(); //返回队列的头部元素
//System.out.println(temp.toString());
queue.poll(); //移除并返回队列的头部元素
list.add(temp.val);
if (temp.left!=null) {
queue.add(temp.left); //将左孩子节点压进去
}
if (temp.right!=null) { //将右孩子节点压进去
queue.add(temp.right);
}
count --;
}
for (Integer integer : list) {
// System.out.println("**"+integer);
levelResult.add(integer + "");
}
}
}
//中序遍历
private static void inTraverseBinTree(TreeNode tree) {
if (tree == null) {
return;
}
if (tree.left!=null) {
inTraverseBinTree(tree.left);
}
inResult.add(tree.val + "");
if (tree.right!=null) {
inTraverseBinTree(tree.right);
}
}
//先序遍历
private static void preTraverseBinTree(TreeNode tree) {
if (tree == null) {
return ;
}
preResult.add(tree.val+"");
if (tree.left!=null) {
preTraverseBinTree(tree.left);
}
if (tree.right!=null) {
preTraverseBinTree(tree.right);
}
}
打印结果为：
先序遍历为：[1, 2, 4, 7, 3, 5, 6, 8]
中序遍历为：[4, 7, 2, 1, 5, 3, 8, 6]
后序遍历为：[7, 4, 2, 5, 8, 6, 3, 1]
层次遍历为：[1, 2, 3, 4, 5, 6, 7, 8]
全文代码详见：BinaryTree