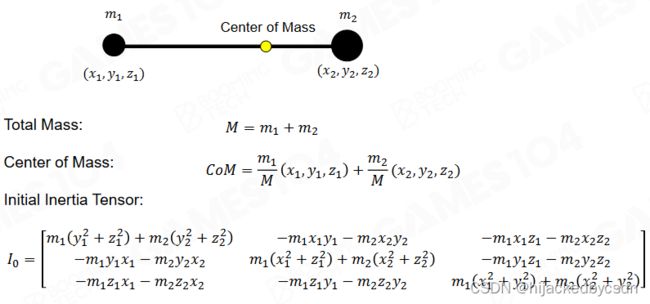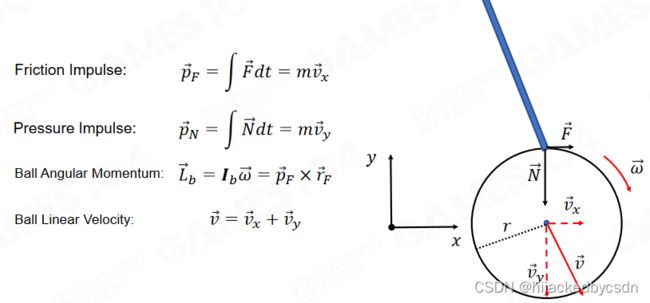Games104 学习笔记 8~11

课程 PPT

https://games-cn.org/games104-slides/

第八节 游戏引擎的动画技术基础

Challenges in Game Animation

和电影行业中的计算机动画相比，游戏中的动画难点之一在于游戏是一个和玩家不断互动的过程。游戏开发者很难预设玩家的行为，而且必须考虑玩家的行为与场景进行互动的结果。

同时，游戏对于实时性有着更高的需求。在很多情况下我们甚至需要考虑游戏场景中有着上万个单位同时进行运动的情况，这样大规模的计算给游戏动画系统的性能造成了巨大的挑战。

除此之外，玩家对于现代游戏角色的动画也提出了更高的要求。我们希望游戏角色有着更加生动的表情，同时在运动过程中的行为尽可能自然。

2D Animation Techniques in Games

Sprite animation

Live2D

Live2D技术的核心是把角色的各个部位分解成不同的元素，通过对每个元素进行变形来实现虚拟人物的不同动作。

在放置不同元素时还可以通过对图层顺序的变化进一步提升表现力。

对于每一个图元则需要事先设置好它的网格来控制形变，这样角色的不同动作就可以通过对网格控制点的运动来进行描述。

最后根据关键帧把角色不同元素不同控制点的运动组织起来就完成了一个虚拟角色的动作。

3D Animation Techniques in Games

Degrees of Freedom

对于刚体而言描述它的运动需要 3 个平动和 3 个旋转一共6个自由度。

Rigid Hierarchical Animation

最简单的 3D 动画技术是把角色的不同部位都视为刚体，然后按照一定的层次把它们组织起来。早期的 3D 游戏就是使用这样的方法来实现三维角色的不同行为。

但是刚体之间可能会穿插

Per-vertex Animation

另一种实现三维动画的方法是利用网格的顶点来控制运动，这种技术称为顶点动画(per-vertex animation)。此时网格上的每个顶点有具有3个平移自由度，通过对网格顶点坐标的变换就可以实现模型的运动。这种动画方法在人物角色上的应用比较少，但在物理仿真中则相对比较常见。

布料，水流，都可以用顶点动画来做

Morph Target Animation

类似于顶点动画，morph target animation 同样是利用顶点来控制模型的运动。和顶点动画不同的是，morph target animation 不会直接操作网格顶点的坐标而是通过顶点的位置和权重来控制整个网格的行为。morph target animation 在表现角色面部表情上有很广泛的应用。

Skinned Animation

经典刷权重

也可用于 2d

Physics-based Animation

基于物理法则的动画模拟

也可以做布料，水流

也涉及 IK

Animation Content Creation

使用关键帧

Skinned Animation Implementation

接下来我们介绍蒙皮动画的实现细节。从整体上来看，蒙皮动画的实现包括以下5个步骤：

1. 建立网格模型；

2. 建立网格模型附着的骨骼；

3. 为网格上每个顶点赋予骨骼对应的权重；

4. 利用骨骼完成角色的运动；

5. 结合顶点的骨骼权重实现网格的运动。

上述步骤看上去不是很难，但在实际编程中需要多加小心防止出现网格爆炸的问题。

Different Spaces

要描述骨骼的运动我们还需要引入相应的坐标系统。首先整个游戏世界定义了一个世界坐标系(world space)，所有的物体都位于这个坐标系中；对于每个单独的模型，模型自身还定义了一个模型坐标系(model space)；最后每个骨骼还定义了一个局部坐标系(local space)来描述网格顶点和骨骼的相对位置关系。任意两个坐标系之间的变换关系可以通过3个平移和3个旋转一共6个自由度来表示，这样每个顶点的坐标都可以从局部坐标系变换到模型坐标系再变换到世界坐标系上。

Skeleton

在此基础上就可以结合角色自身的特点构建出具有一定拓扑关系的骨骼模型(skeleton)，这一般可以通过一棵树来表示。对于类人型的骨骼，整棵树的根节点一般位于胯部。而对于四足动物等其它类型的骨骼其根部则会位于其它位置。

Joint

我们定义骨骼与骨骼之间相连接的部位为一个关节(joint)。实际上我们不会直接按照骨骼进行编程，而是利用关节及他们直接的连接关系来表达整个骨骼的运动。

还有一个为什么不用 bone 描述的理由就是，假设想象一个沿着 Z 轴竖直放置的骨骼，上下两个 joint，底部的 joint 绕 Z 转动 -30 度，顶部的 joint 绕 Z 转动 30 度，这根骨骼实际上发生了扭转 twist，而单独对于一个刚体，一般的数据结构都没有描述扭转量的

在游戏建模中除了常见的四肢外可能还会根据角色的服装和特点来构建更加复杂的骨骼模型。比如说玩家手中的武器就是通过在角色手上绑定一个新的骨骼来实现的。

除此之外，在进行建模时我们往往还会定义一个root关节。不同于前面介绍过的胯部骨骼，root关节一般会定义在角色的两脚之间，这样方便把角色固定的地面上。类似地，对于坐骑的骨骼也往往会单独把root关节定义在接近地面的位置。

很多游戏动画需要将不同的骨骼绑定到一起。最直观的例子就是角色骑马的动画，此时角色和马都有自身独立的动画而我们需要将它们组合到一起完成角色骑马的动作。要实现这种功能需要设计一个单独的mount关节，然后通过这个关节将两个模型拼接到一起。需要注意的是在拼接时不仅要考虑关节坐标的一致性，更要保证两个模型的mount关节上有一致的朝向，这样才能实现模型正确的结合。

Bind Pose

早期的骨骼建模会使用T-pose作为角色动作的基准。但在实践过程中发现T-pose会导致角色的肩部出现挤压的状况，因此现代3A游戏中更多地会使用A-pose这种姿势进行建模

Skeleton Pose

完成骨骼建模后，角色的运动就可以通过骨骼的姿态(pose)来进行描述。这里需要注意的是表达角色的不同动作时每个关节实际上具有9个自由度，除了刚体变换的6个自由度外还需要考虑3个放缩变换引入的自由度。这3个放缩自由度对于表现一些大变形的动作起着很重要的作用。

Math of 3D Rotation

2D Orientation Math

在这一节中我们会详细介绍三维空间中如何表示物体旋转这一问题，不过首先我们来回顾一下二维空间的旋转。对于二维空间中的点 $(x,y)$，当它绕原点进行旋转时只需要一个旋转角度 $\theta$ 就可以进行描述，旋转的过程可以通过一个旋转矩阵 $R(\theta )$ 来进行表示。

3D Orientation Math

Euler Angle

三维空间中的旋转要更复杂一些。我们可以把任意三维空间的旋转分解为绕三个轴的旋转，每个旋转都对应一个三维旋转矩阵，这样就可以通过绕三个轴的旋转角度来进行表达。这种描述三维旋转的方法称为欧拉角(Euler angle)。

欧拉角在很多领域都有大量的应用，比如说飞行器的导航和姿态描述一般都是基于欧拉角的。

但是需要说明的是欧拉角有很多局限性，比如说欧拉角是依赖于旋转顺序的。在使用欧拉角时必须指明绕三个旋转轴进行旋转的顺序，同样的欧拉角按照不同的顺序进行旋转会得到不同的结果。

欧拉角的另一个缺陷在于万向锁(gimbal lock)：在有些情况下按照欧拉角进行旋转会出现退化的现象，导致物体的旋转会被锁死在某个方向上。

总结一下，欧拉角的主要缺陷如下：

1. 万向锁及相应的自由度退化问题；

2. 很难对欧拉角进行插值；

3. 很难通过欧拉角对旋转进行叠加；

4. 很难描述绕$x,y,z$轴之外其它轴的旋转。

由于这些缺陷的存在，游戏引擎中几乎不会直接使用欧拉角来表达物体的旋转。

Quaternion

在游戏引擎中更常用的旋转表达方式是四元数(quaternion)，它由 Hamilton 爵士于19世纪提出。

我们知道二维空间中的旋转可以使用复数来进行表示。换句话说，二维平面上的旋转等价于复数乘法。

类似地，我们可以认为四元数是复数在三维空间的推广。一个四元数 $q$ 具有1个实部和3个虚部 $i,j,k$，四元数的运算法则如下：

它用群论证明了，只有在三维空间中，四元数这种，一个自由度就加一个虚部的想法才能 work

已知 ijk = -1，那么 ij 等于多少？ijk^2 = -k 得 ij = k

点乘就是向量点乘，只是可以写成矩阵形式

四元数的逆表示它的相反方向的旋转

可以证明，任意的三维旋转可以通过一个单位四元数来表示。当我们需要对点$\mathbf{v}$进行旋转时，只需要先把$\mathbf{v}$转换成一个纯四元数，然后再按照四元数乘法进行变换，最后取出虚部作为旋转后的坐标即可：

旋转是前后各夹一个

进一步可以证明用欧拉角表达的旋转都对应着一个四元数的表示。同样地，四元数与旋转矩阵直接也存在着相应的转换关系。

这个 $v^{\prime }=qv{q}^{-1}$ 居然能够变成一个 $v^{\prime }=Mv$……是我线代弱了……有点不懂怎么变的

使用四元数来表达三维旋转的优势在于我们可以使用简单的代数运算来获得旋转的逆运算、旋转的组合以及两个单位向量之间的相差的旋转量。

对于绕任意轴旋转的情况，我们同样可以利用旋转轴和旋转角度的信息来构造出四元数进行表达。

Joint Pose

Affine Matrix

有了三维旋转的表达方法后我们就可以利用关节的姿态来控制角色模型的运动。具体来说，我们每个关节的姿态可以分为平移、旋转和缩放三个部分，把它们组合到一起就可以通过一个仿射矩阵(affine matrix)来描述关节的姿态。

平移比如 root 骨骼固定在地面位置嘛，然后与胯部之间的位置会实时变

缩放比如面部骨骼

对于骨骼上的每一个关节，我们实际上只需要存储它相对于父节点的相对姿态。这样在计算绝对姿态时可以利用仿射矩阵的传递性从根节点出发进行累乘即可。

这种利用相对坐标系来描述位姿关系的好处在于它可以正确地对角色动作进行插值，而如果直接从绝对坐标系进行插值则会得到错误的结果。

Skinning Matrix

在前面我们介绍过模型的每个顶点是附着在骨骼上的，因此在关节姿态发生变化后顶点会跟着关节一起运动。

记顶点 $V$ 在关节 $J$ 定义的局部坐标系下的坐标为 $V_b^l$，初始时刻进行绑定时 $V$ 在模型坐标系下的坐标为 $V_b^m$。在 $t$ 时刻，当关节位姿发生变化后顶点的局部坐标保持不变。此时顶点在模型坐标系下的坐标和局部坐标直接满足变换关系：

$$V^l(t)=V_b^l=(M_{b(J)}^m{)}^{-1}{V}_b^m$$

其中 $M_{b(J)}^m$ 即为初始时刻进行绑定时关节 $J$ 对应的姿态。

利用 $t$ 时刻关节的位姿 $M_J^m(t)$，可以得到顶点 $V$ 模型坐标系下的坐标 $V^m(t)$ 与初始时刻模型坐标系下绑定的坐标 $V_b^m$ 之间的变换关系：

$$V^m(t)=M_J^m(t)V_J^l=M_J^m(t)\cdot (M_{b(J)}^m{)}^{-1}{V}_b^m=K_J{V}_b^m$$

其中 $K_J=M_J^m(t)\cdot (M_{b(J)}^m{)}^{-1}$ 称为关节 $J$ 的蒙皮矩阵(skinning matrix)。

这就是绑定的 joint 的仿射矩阵乘上代表绑定关系的矩阵

注意到蒙皮矩阵的第二项包含矩阵求逆运算，在游戏引擎中为了提高计算效率一般会直接存储整个逆阵。

Skinning Matrix Palette

角色身上的顶点数会有几万个，但是骨骼数就几十个，所以蒙皮矩阵要被调用很多次，所以要先算好

先把所有骨骼的位置算好，然后再把所有骨骼的蒙皮矩阵算好。所有骨骼的蒙皮矩阵还要乘上一个模型坐标系到世界坐标系的仿射矩阵

Weighted Skinning with Multi-joints

对于同一个顶点绑定到多个骨骼的情况则需要通过插值进行处理。此时顶点$V$会同时存储它所绑定到的关节以及对应的权重，其在世界坐标系下的坐标为它在每个关节上定义的局部坐标转换到世界坐标后的加权和。

插值是在模型空间中插值

Interpolation

在动画制作过程中一般只会记录下一系列关键帧上骨骼的姿态，而要得到实际的动画还需要通过插值来获得中间帧上模型的运动。

Clip

Interpolation between Poses

Simple Interpolation of Translation and Scale

线性插值是最基本的插值方法，我们可以通过对关节姿态的插值来计算中间帧上的模型运动。

Quaternion Interpolation of Rotation

对于三维旋转的插值要相对复杂一些，不过我们可以借助四元数的运算来进行处理。要获得插值后的旋转只需要对四元数直接进行线性插值，然后再进行归一化即可，这样的方法称为 NLERP。

一般的插值是沿着最短路的，这里做一个运算，如果是大于 0 就直接插值，如果是小于 0，那么反向插值，来避免一直找最短路

NLERP 并不是真的对旋转进行线性插值。当动画的帧数较高时 NLERP 会有明显的违和感，这是由于它没有考虑旋转并不是线性空间。

想要真的对旋转进行线性插值可以使用SLERP这样的算法，不过SLERP的计算代价要比NLERP要大一些。

因为这里用到了反三角函数，反三角函数会比较费，因为它的计算需要查表

又因为 $\theta$ 很小的时候，$\theta \sim \sin \theta$，它作为分母可能不稳定

所以一般旋转角 $\theta$ 比较大的时候使用 SLERP，旋转角比较小的时候使用 NLERP

AnimationRuntime Pipeline

更多东西也可以在 GPU 中算

Animation Compression

实际上直接存储每个模型上每个关节的姿态需要占用非常多的资源，因此利用一些压缩技术来减少动画存储空间有着非常重要的意义。

DoF Reduction

在广泛的实践中人们发现不同关节不同自由度的信号之间有着巨大的差异。以大腿关节为例，在大多数情况下它的缩放自由度都是1而且大部分的平动自由度都是0，它的运动基本都是来自于旋转；而对于手指这样的关节，它的旋转很少但是平动会相对多一些。

因此最简单的动画压缩方法是直接缩减运动的自由度，把关节的缩放和平动自由度直接去掉只保存旋转。

一般是面部才有缩放；骨盆 peivis，面部，其他特殊骨骼才有平移

Keyframe

对于旋转自由度我们可以使用关键帧(keyframe)来对信号进行离散，然后通过插值来重建原始信号。

在离散时还可以利用不等间距采样的方式来进一步压缩信号。

直接使用线性插值来描述非等间距采样的旋转信号仍然不够自然，这里推荐使用 Catmull-Rom 曲线来对关键帧进行插值。Catmull-Rom 曲线只需要一个锐度参数 $\alpha$ 以及4个控制点就可以获得C1连续的光滑曲线。基于 Catmull-Rom 曲线可以实现非常高精度的信号离散和重建效果。

Quantization

进一步压缩数据时还可以考虑使用低精度的存储方式来记录位移信号。比如说可以通过规范化的方法将32位浮点数转换为16位无符号整数来表示，这样虽然损失了一些精度但却可以极大地减少存储空间。

转换精度的过程就是，先转换到 0 到 1 的范围，然后换精度，然后重新映射回去

对四元数进行压缩时可以利用单位四元数每一位上数值的范围来进行化简。具体来说我们可以首先使用 2 个 bit 来表示四元数的哪一位被丢掉了，剩下的 3 位可以分别使用 15 个 bit 来进行表达。这样一个四元数可以使用 48 个 bit 来进行存储，远小于使用 4 个 float 所需的 128 个 bit。

Error Propagation

数据压缩必然会导致精度损失的问题。对于一些末端的关节，由于误差传播的效应可能会产生非常大的累计误差。这种现象的直观反映就是模型可能会产生视觉上可见的偏移。

要缓解这种累计误差首先需要定量化的描述误差。

误差可能发生在平移，旋转，缩放上

一般需要的是视觉误差

我们可以直接对比数据压缩前后模型每个顶点上的坐标差异，但这种做法的计算代价过于巨大，目前工业界的主流处理方法是在关节上设置虚拟顶点然后利用虚拟顶点压缩前后的差异来描述误差。

而要缓解累计误差我们可以为不同的关节设置不同的存储精度，或是通过主动补偿的方式来进行修正。总体而言，对于累计误差目前没有非常完善的处理方法。

本来骨骼动画是一个平滑的插值，现在进行误差补偿之后，每一个骨骼的频率不一样，补偿得到的结果会发生高频抖动

所以还需要 Forward IK

Animation DCC Process

一般来说蒙皮动画的制作包括建立网格模型、绑定骨骼、蒙皮、制作骨骼动画以及导出等步骤。

Mesh building

动画制作的第一步是建立网格模型。一般来说建模师设计的三维模型会具有远高于动画需求的精度，因此在动画制作阶段往往只会使用低精度的模型进行处理。

需要注意的一点是为了保证最终动画成品的效果，建模师在建模时一般会在关节处对网格进行加密。

接下来需要为模型制作骨骼，目前主流的三维建模软件都集成了骨骼的功能。在角色基本骨骼的基础上一般还会根据游戏玩法进一步添加一些额外的关节，包括武器、坐骑等。

然后我们需要把顶点绑定到骨骼上，这一般需要在软件自动计算的基础上结合建模师的经验进行手动校正。

在动画建模阶段则需要由动画师根据关键帧设置模型的动作。

root 的位置会变，一般这个 root 的位移会存为位移曲线，提供给引擎用

最后游戏引擎需要提供相应的模型导出功能。目前工业标准是使用FBX格式来保存动画所需的全部几何运动数据。

QA

顶点绑定的关节有数量限制吗

原则上没有，但是为了计算效率可能会限制，比如用一个 bit 来存绑定的关节，也就是 256 个关节

骨骼和场景碰撞的动画是怎么做得

骨骼用圆柱碰撞

原来的动画在检测到刚体碰撞之后可以切成另一套表现碰撞效果的动画

Morph Target Animation 与 Skinned Animation 是不是只是侧重点有所不同？

Skinned Animation 动的是骨骼

Morph Target Animation 动的是顶点

第九节 高级动画技术：动画树、IK 和表情动画

别人的记录

https://peng00bo00.github.io/2022/05/17/GAMES104-NOTES-09.html

Animation Blending

基于 DCC 流程我们可以获得不同的动画资源，然而这些资源往往是相互独立的，在实际游戏中我们还需要将不同类型的动画混合起来以实现更加自然的运动效果。以角色的跑动为例，人体的跑动包含低速的步行以及高速的跑动两个部分的动画。将两个动画混合起来就可以实现自然的变速效果。

要实现动画的混合非常简单，我们只需要对骨骼的姿态进行插值即可。但和上节课介绍的关键帧插值不同，在进行动画混合时不仅需要考虑同一组动画关键帧之间的插值，还要考虑不同组动画不同关键帧的插值。

计算插值权重也比不是很难，我们可以按照当前角色运动的速度来选择两个相邻动作的关键帧。两个动作的权重即为对速度进行线性插值的权重。

就是，这个物理量和相应的区间端点的选取是艺术家选的，可以配的

在进行动画混合时还要考虑时间线上对齐的问题。要使插值后的动作更加自然，我们需要动画师在动画建模时将每个动画都按照无限循环播放的形式进行设计。同时，两组进行混合的动画最好要保证角色具有相同的肢体运动频率。这样可以保证混合后的动画更加自然，不会出现角色滑行的结果。

Blend Space

上面介绍的动画混合技术主要针对的是角色一维运动，我们可以基于同样的思想把角色在平面上的运动动画进行混合，进而获得角色不同方向上的连续动画。

对骨骼动画进行插值的方法也很简单，只要根据角色运动的状态在两个方向上分别进行线性插值即可。

有时动画师会为角色的平面运动建立多个不同的预设 clip，在这种情况下直接进行插值是比较困难的。为了解决这种问题我们可以利用 Delaunay 三角化的方式对平面进行划分，在需要对动作进行插值时首先选择动作所在的三角形，然后再利用重心坐标进行插值即可。

Skeleton Masked Blending

除了平面运动外，有些角色的动作可能只依赖于一部分骨骼。以鼓掌动作为例，角色在鼓掌时只涉及上半身的骨骼运动而与下半身无关，因此我们可以把上半身鼓掌的动作融合到其它下半身动作中。

要进行这样的处理也十分简单，我们也有设置一个mask来标记混合动画时需要考虑角色的哪些骨骼。这样就可以单独录制不同的动作然后根据需要组合出新的动作。

Additive Blending

角色动作另一种常见的情况是动作本身只与关节相对姿态有关，而与绝对姿态无关。以点头动画为例，角色在点头时可以有不同的朝向，但在录制动画时只需要一套统一的动画。要处理这种情况则需要在保存动画时指明这个clip是只依赖于相对位姿的动画，在实际进行动画混合时再根据角色当前的姿态叠加上相对位姿。

使用这种 additive blending 技术时需要额外注意角色的姿态，尤其要避免角色关节的姿态超过最大值的情况。

Action State Machine (ASM)

在很多时候角色的动作不能直接通过对动画进行插值来获得。以跳跃为例，实际上角色的跳跃动作可以划分为起跳、浮空以及落地三个不同状态。不同的状态之间存在着一定的依赖关系，这会使得我们可能无法通过直接插值的方式来计算角色当前的动作。

实际上我们可以把角色的动作和状态视为图上的节点，这样角色的运动就等价于在不同节点之间进行游走。这种模型称为动作状态机(action state machine, ASM)。

当玩家发出指令后，角色根据指令和预设的状态转移条件来判断是否需要转移到其它的状态。当确定需要发生转移时就可以根据动画师的设计来切换角色的动画。

在切换角色动画时根据切换的方法可以分为 smooth transition 和 frozen transition 两种。进行 smooth transition 时，我们需要使用前面介绍过的动画混合插值方法逐步从一个动画过渡到另一个动画；而需要进行 frozen transition 时，我们则会停住角色当前的动画然后根据设置直接切换到下一个动画。这两种动画切换形式在游戏工业中都有广泛的应用。

同时，在进行 smooth transition 时可以根据动画师的需要设计不同的过渡曲线来表达不同的动画切换效果。

动作状态机技术已经广泛应用于各种游戏引擎中。

同时在游戏业界还结合了多层次的设计将角色身体的不同部位单独设计成状态机，这样可以实现更加丰富的角色肢体动作。

Animation Blend Tree

在 ASM 的基础上现代游戏引擎还引入了动画树(animation blend tree)的概念。动画树可以理解为一棵表达树，它可以对不同的动画资源按照指定的计算规则进行混合，从而产生新的动画。

以线性插值为例，我们可以把 LERP 运算看做是一个节点，它将两个输入的动画资源按照比例混合到一起。基于动画树的结构可以在 LERP 的基础上定义更加复杂的动画混合插值计算。类似地，前面介绍过的 additive blending 也可以看做是一种特殊的运算节点，通过该节点可以在原始动作上叠加一个新的动作。

使用动画树来描述动画混合的优势在于它可以基于简单的树状结构描述复杂的动画混合过程，比如说 layered ASM 就可以看做是不同动画资源在相应层级上进行混合的结果。

同时，动画树还可以看做是一种递归的计算结构。我们可以在游戏引擎中将各种不同的动画生成方法都定义为动画树的节点，在一个计算节点中可以包含很多更复杂的计算过程，甚至是小型的动画树。这样的结构形式会为设计师提供更高的设计自由度，从而实现复杂的动画效果。

虚幻引擎中同样实现了动画树的功能。游戏开发者和设计师可以利用大量的计算节点来自定义角色的不同行为。

动画树的一个核心在于使用控制变量(control parameters)来改变输出动画的结果。一般来说控制变量来源于游戏的玩法系统，当控制变量发生改变时动画树会根据自身定义的规则动态地调整动画混合的比例以及使用的动画资源。

还是以虚幻引擎为例，虚幻引擎中使用variable作为动画树的控制变量调整不同动画之间的混合比例。此外，虚幻引擎中还使用了event作为资源切换的信号，当动画树接收到某个event后会调整自身的动画资源实现角色动画状态的改变。

Inverse Kinematics (IK)

我们目前介绍过的动画系统都是之间利用骨骼和关节的运动学公式来驱动角色的动作，这种方式称为前向运动学(forward kinematics, FK)。在很多情况下我们还需要考虑游戏场景对于角色肢体的约束，并且利用这些约束来求出角色合适的骨骼关节姿态，这种动画技术则称为反向运动学(inverse kinematics, IK)。IK 在游戏中有着非常丰富的应用场景，比如说角色在崎岖不平的地面上行走时我们根据地面的起伏来调整前进的动画。

Two Bones IK

IK 最简单的情况是只考虑角色两块骨骼的运动，然后利用约束来求解关节的姿态。这种问题的解法其实非常简单，我们可以利用骨骼的大小以及场景约束来构造三角形，然后利用几何关系来求解出所需的姿态。

当然在三维空间中我们基于上述方法实际上会得到无穷多组解，因此在实际计算中还要引入一些额外的约束来保证解的位移性。

例如这里，两个球的交线上有无数个可能点

通过一个 reference vector 来确定取哪个点

Multi-Joint IK

在 IK 问题中更常见的情况是链式的关节，此时我们需要求解出末端到达指定位置时每个关节对应的姿态。

除此之外，在实际求解前还需要考虑解的存在性。很多时候可能并不存在能够满足需求的关节姿态。

另一方面，角色的不同关节往往还具有不同类型的约束。在进行求解时需要考虑这些约束，否则会出现角色动作过于扭曲的状况。

总体来看，在三维空间中求解带约束的IK问题是非常复杂的，目前还没有通用的算法来进行实时求解。在现代游戏引擎中一般是通过一些启发式的算法来进行近似求解。

CCD

CCD(cyclic coordinate decent)是目前游戏引擎中求解IK问题最主流的算法。它的求解过程非常简单：在每次迭代中按照关节顺序对当前关节进行旋转，使得末端关节指向目标位置。

在标准CCD算法的基础上还可以对迭代过程进行优化，比如设置tolerance region控制每次旋转的角度，或是对接近根部关节的旋转施加额外的约束从而保证根部不会出现过大的旋转。

他这样的优化思路，本质上就是把每一个骨骼看成弹簧，每一次旋转关节都是对弹簧进行拉伸，现在要求弹簧的势能最小

FABRIK

FABRIK(forward and backward reaching inverse kinematics)也是一种经典的IK求解算法。它的思想是在每一轮迭代中进行一次前向计算以及一次反向计算：前向计算时从末端关节向根部关节移动骨骼，而在反向计算时则从根部出发向末端移动关节。通过不断迭代同样可以计算出合适的姿态。

在前向计算或者是反向计算的时候，首先是给定第一个目标点，然后移动关节，但是认为这个时候骨骼的长度是不变的，所以这个骨骼的一个关节移动到目标点之后，骨骼的另外一个关节的位置就作为下一个关节的目标点，依次类推

例如在前向计算的时候，从前向的一个目标点一路往后面的关节推，最后递推到根节点的移动，然后进入后向计算，认为这个根节点不应该动，于是把根节点移动之前的位置作为目标点，移动到目标点，也就是把根节点再拉回来，然后关节的移动往前面的关节递推

一般用 CCD，可能是因为 CCD 好加角度约束？也不一定吧我个人觉得，FABRIK 也可以做角度约束，例如

这里，如果角度存在约束，就可以算出移动的最大范围，如果目标点在这个范围之外，那么这个关节就不移动，递归到下一个关节让他尝试移动

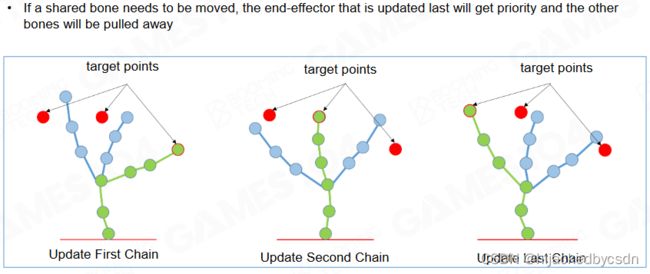
Multiple End-Effectors

多个 IK 存在时可能存在冲突，也就是多个 IK 的目标点之间不能连续地视线

可能是用一个优先级或者权重混合

IK with Multiple End-Effectors

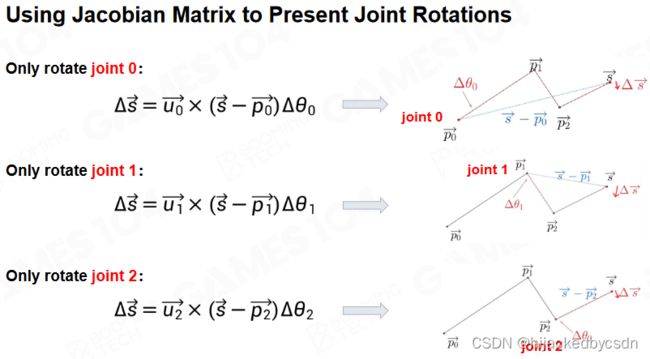
Jacobian Matrix

Jacobian矩阵(Jacobian matrix)是一种基于优化来求解IK问题的算法，它在机器人学中有着非常广泛的应用。关于 Jacobian 矩阵的细节我们会在后面的物理系统中进行详细的介绍。

若干个 joint 的角度记为 x 向量，若干个 joint 空间上的位置记为 x 的函数，这个函数也是一个向量，向量元素是 vector3f

每一次向着目标点走 $\Delta x$，各个关节进行微小的旋转，最后不断逼近目标点

Other IK Solutions

1.基于物理的方法 Physics-based Method

更加自然

但是需要很多计算

2.PBD(Position Based Dynamics)

3.Fullbody IK in UE5

XPBD（Extended PBD）

IK 的其他问题：需要提前察觉环境，需要考虑身体的物理平衡

Updated Animation Pipeline with Blending and IK

同时需要注意的是 IK 也需要整合到动画管线中作为后处理来调整骨骼和关节的姿态。

Facial Animation

表情动画是动画系统中的重要组成部分，从人体的生理学基础来讲表情是由面部肌肉的运动来进行控制的。

而表情动画的难点在于人的表情变化往往只有非常少的肌肉运动，换句话说不同面部表情之间的差异可能是非常细微的。

FACS

得益于电影工业对面部表情的探索，人们发现只需要面部五官进行组合就可以表现出不同的表情。这种表达表情的方式称为 FACS(facial action coding system)，它一共包含 46 组基本单元。

同时由于面部的对称性，实际上在制作表情动画时只需要一半左右的单元就可以表达不同的表情。

Key Pose Blending

基于FACS就可以着手制作不同的表情动画了。在表情动画中我们一般是直接使用面部的网格而不是骨骼关节系统来描述表情，不过动画插值的思想和骨骼动画是一致的。

进行表情混合时需要注意直接对面部进行混合往往会得到错误的结果，这是由于人脸在表达不同表情时一般只会用到一小部分面部肌肉，直接对表情进行混合容易造成整个面部发生运动。要解决这个问题也十分简单，只需要存储一个基本表情然后利用前面介绍过的 additive blending 技术对表情进行叠加即可。

现在一般用 Morph Target Animation 做面部动画

骨骼动画也可以做面部动画，使用骨骼动画的优势在于它比较适合表达面部比较大的变形，比如说眼球的转动或是嘴巴张开以及游戏中常见的捏脸系统等等，但是像嘟嘴这种变形动画，一般做的都不自然

UV Texture Facial Animation

使用贴图来表达面部动画，这种方法在很多卡通渲染的游戏中有着大量的应用。

Muscle Model Animation

真实地使用肌肉运动来表达

尽管这种方法还没有大规模应用在游戏业界，而且它的计算需求也远高于传统方法，但它却可以实现更加逼真的角色表情。

Metahuman

Animation Retargeting

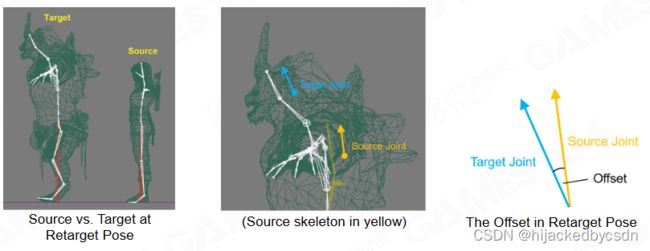
本节课最后介绍了动画重定向(animation retargeting)技术在游戏行业中的应用。在动画制作中动画师往往只会对同一个动作进行一次建模，而在游戏中设计师则希望可把这个动作应用到各种不同的角色中。这种把一组动作从一个角色迁移到另一个角色的技术称为动画重定向，其中已经绑定好动作的模型称为源角色(source character)而需要施加动画的角色称为目标角色(target character)。

动画重定向最直接的做法是把对应骨骼和关节的动作直接复制过去。当然考虑到源角色和目标角色骨骼之间位置的差异，一般需要对关节姿态进行一定的补偿。

考虑到不同角色之间姿态的差异，在进行重定向时可以只施加关节的相对运动。这种做法会得到更加自然以及符合人直觉的动画效果。

综合上面的内容就得到了动画重定向最基本的算法：处理关节旋转时我们考虑关节的相对旋转，处理骨骼的平移时则需要根据目标角色骨骼的实际长度进行补偿，而对于缩放的情况则直接按照比例进行缩放。这样就可以把源角色的动作迁移到目标角色身上。

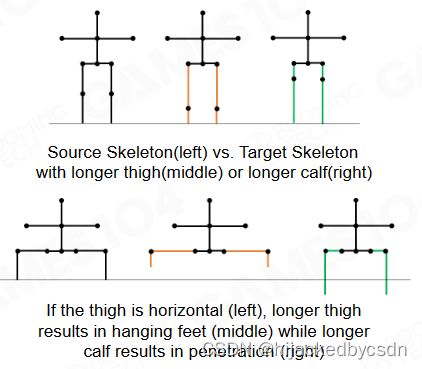
Lock Feet by IK after Retargeting

在实际工程中人们发现基于上面介绍的算法进行重定向时，由于源角色和目标角色本身骨骼的差异强行迁移动作容易造成目标角色悬空的现象。因此还需要对角色的高度再进行一定的补偿。

对高度补偿之后，步频可能也要变。因为高度 * 步频等于每步所走长度，补偿高度之后，如果步频不变的话，那么得到的每步所走长度就会变，如果人物模型还按照原来的刚体速度移动，就会出现滑步的情况

但是有些时候单纯对高度补偿只对走路有用，对其他动作，比如蹲下，还需要分情况讨论

所以为了适应重定向后各个动画的微调需求，需要 IK 来把脚锁在地上

当然也有一些离线软件可以做重定向，做得比较好

Retargeting with Different Skeleton Hierarchy

目前介绍的重定向方法都假定了源角色和目标角色的骨骼有相同的拓扑结构，但在很多情况下两个角色的骨骼是没有办法做到一一对应的，此时就需要一些更复杂的算法来传递动画。

Easy Solution

比较直接的处理方法是利用骨骼和关节的对应关系来对关节运动进行插值，这样就可以把原始骨骼的动作重定向到新的骨骼上。实际上在Omniverse上就使用了类似的方法来处理动画重定向的问题。

具体来说，假设我找到了要重定向的 3 根骨骼与源骨骼的 4 根骨骼中的 3 根对应，那么我就把源骨骼的位置沿骨骼做一个 0 到 1 的坐标系，重定向的骨骼也是，然后在源骨骼的坐标系上寻找重定向的骨骼的关节的坐标，取到相应的位置，付给重定向的骨骼的关节

当然动画重定向仍然是一个相对比较复杂的问题，很多时候即使把源角色的动作迁移到目标角色上仍然会出现很多穿模或者相交的问题。在这种情况下一般还需要动画师对迁移后的动画进行一些微调。

例如在女性骨骼上手与腰不相交，但是在其他角色上腰的宽度更大，就发生了手与腰相交

例如鼓掌这个动作是具有语义的，两掌之间是需要贴合的，但是重定向之后可能两掌没有贴合在一起

Morph Animation Retargeting

Morph Animation 也可以重定向

Morph Animation 的重定向也有问题，例如重定向的脸部的眼睛比源脸部的眼睛大了一点，那么原来的闭眼动作可以完全合上眼睑，现在重定向之后不能完全合上了

可以对网格施加一些额外的约束来强行获得正确的动画效果。

例如人为设置控制点，如果发现控制点没有重合，就使用拉普拉斯算子，通过几个点将周围的点弹性地拉上来

Q&A

有没有三维的 blend space

应该有，但是没看到使用

面部动画是不是也是通过顶点动画做的

纹理，骨骼，顶点都有

动画领域里有哪些最前沿的问题？

自然的 IK

Animation 的 Blending

第十节 游戏引擎中物理系统的基础理论和算法

Physics Actors and Shapes

Actor

在物理引擎中根据对象自身的特点我们可以把它划分为静态对象、动态对象等。其中静态对象是指在仿真过程中不会发生改变的对象，比如说游戏中的地面、墙壁等等；与之对应的是动态对象，它们的运动状态会在游戏过程中动态地进行变化，而且它们的运动过程需要符合相应的动力学模型。

除此之外游戏角色和场景的互动还需要相应的trigger，它可以用来改变对象的各种状态。

最后一个常见的物理对象是kinematics，它是指不完全基于物理法则的物理对象，但往往与玩法高度相关。

Actor Shapes

物理对象最重要的属性是它的形状(shape)。比较规则和简单的形状可以通过解析的方法来进行描述：

Spheres

Capsules

Boxes

Convex Meshes

Triangle Meshes

Height Fields

在进行物理仿真时我们首先会把物理对象进行一定的包裹，使用相对简单的几何形状来近似复杂的模型。

Shape Properties

在形状的基础上我们还需要对一些物理量进行定义，包括对象的质量或密度、质心以及物理材质等。

Mass and Density

只有一个静平衡点的物体

Center of Mass

Friction & Restitution

Forces

Force

Impulse

Movements

Newton’s 1st Law of Motion

没有外力时，

$$\begin{gathered} v(t+\Delta t)=v(t) \\ x(t+\Delta t)=x(t)+v(t)\Delta t \end{gathered}$$

Newton’s 2st Law of Motion

当有外力时

$$F=ma$$

$$a(t)=\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{{\mathrm{d}}^{2}x(t)}{\mathrm{d}{t}^2}$$

Movement under Constant Force

当外力为常量时

$$\begin{gathered} v(t+\Delta t)=v(t) \\ x(t+\Delta t)=x(t)+v(t)\Delta t+\frac{1}{2}a\Delta t^2 \end{gathered}$$

Movement under Varying Force

当外力为变力时，

弹簧或者钟摆在外力作用下，摆动的周期，是数学计算的结果，而不是物理的规律（老师为了方便理解的原话

$$\begin{gathered} v(t+\Delta t)=v(t)+{\int }_t^{t+\Delta t}a(t^{\prime })\mathrm{d}{t}^{\prime } \\ x(t+\Delta t)=x(t)+{\int }_t^{t+\Delta t}v(t^{\prime })\mathrm{d}{t}^{\prime } \end{gathered}$$

在物理引擎中一般无法使用解析的方式来计算物体的运动，因此我们需要一些数值计算方法来进行求解。

Example of Simple Movement

位置

朝向

速度

角速度

Explicit (Forward) Euler’s Method

在进行数值积分时，我们可以把时间间隔设置成一个比较小的值然后对被积函数进行累加来近似实际的积分。具体来说，在计算物体的运动轨迹时我们首先计算物体在当前位置上受到的力并且积分得到加速度，然后再利用加速度来更新速度以及物体的位置。这种计算物体运动轨迹的方法称为 Euler 方法(Euler’s method)，也称为显式积分(explicit integration)。Euler 方法实现起来非常简单，但需要注意的是它的本质是使用物体的当前状态来估计下一时刻的运动状态，此时系统的能量是不守恒的。

Implicit (Backward) Euler’s Method

为了提高数值积分的稳定性，人们还开发出了隐式积分(implicit integration)的技术。隐式积分的实现也很简单，只需要在求解加速度和速度时使用下一时刻而不是当前时刻的值即可，同时可以证明此时系统的能量会不断衰减。当然这又引入了另一个问题，即如何计算系统在下一时刻的物理量，这在很多情况下是比较困难的。

在游戏引擎中更常用的积分方法是半隐式Euler方法(semi-implicit Euler’s method)，即在计算加速度时使用当前时刻的力推导下一时刻的速度，而在计算位置时使用刚才计算出的速度再更新位置。半隐式方法有非常高的数值稳定性，广泛应用于各种类型的物理仿真中。

能量衰减在游戏中是可以接受的，可以理解为摩擦力

Semi-implicit Euler’s Method

Rigid Body Dynamics

刚体动力学

有了牛顿定律和数值积分算法就可以开始进行物理仿真了，其中最简单的情况是质点动力学(particle dynamics)。在质点动力学中所有的物体都被抽象为没有具体形状的质点，此时我们只需要按照牛顿定律更新质点的运动状态即可。

在游戏引擎中更为常见的仿真场景是刚体动力学(rigid body dynamics)。和质点动力学不同，刚体动力学仿真需要考虑物体自身的形状，也因此需要在质点运动的基础上引入刚体旋转的相关概念。

Particle Dynamics

Position

Linear Velocity

Acceleration

Mass

Momentum

Force

Rigid body Dynamics

在 Particle Dynamics 相关的变量之外，还有：

Orientation 旋转

Angular velocity 角速度

Angular acceleration 角加速度

Inertia tensor 转动惯量

Angular momentum 角动量

Torque 力矩

Orientation

刚体的朝向(orientation)可以使用一个旋转矩阵或者四元数来表示，它表示刚体当前姿态相对于初始姿态的旋转。

Angular Velocity

角速度(angular velocity)表示刚体绕某个旋转轴旋转的速度，需要注意的是在描述角速度时必须要指明旋转轴。

Angular Acceleration

角加速度(angular acceleration)类似于加速度，不过它描述的是角速度的变化。这里需要说明的是角速度的变化不仅包括绕当前轴转速的变化，它还包括旋转轴发生变化的情况。

Rotational Inertia

转动惯量(rotational inertia)类似于质量，它描述了刚体抵抗旋转的能力。转动惯量与质量的一大区别在于转动惯量不是一个常数而是一个张量(矩阵)，当刚体的朝向发生改变时需要利用旋转矩阵来计算当前姿态下的转动惯量；同时转动惯量也与刚体上的质量分布密切相关。

$$I=R\cdot I_o\cdot R^T$$

Angular Momentum

角动量(angular momentum)则描述了刚体旋转的状态，它是转动惯量与角速度的乘积。

$$L=Iw$$

空间一致性 -> 动量守恒

朝向一致性 -> 角动量守恒

Torque

当外力不通过刚体的质心时会产生力矩(torque)，从而导致刚体发生旋转。

$$\tau =r\times F=\frac{\mathrm{d}L}{\mathrm{d}t}$$

Summary

在质点动力学的基础上把旋转部分也考虑进来对物体的运动状态进行更新就得到了刚体动力学的仿真方法。

Application：Billiard Dynamics

以台球游戏模拟为例，我们假设台球自身与桌面没有摩擦，这样台球的运动可以简化为二维平面运动。在进行仿真时需要把球杆给予台球的力(冲量)移动到球心来计算台球沿球杆方向的速度；同时这种移动还会对台球施加一个力矩使台球产生旋转，因此也需要更新台球的角速度。

Collision Detection

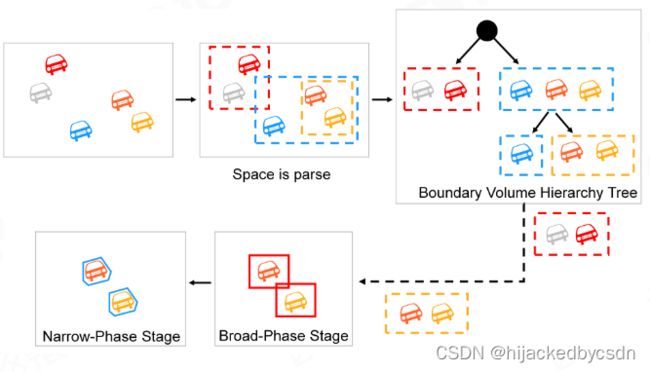
Collision Detection – Two Phases

在进行刚体仿真时我们需要考虑不同刚体之间的相互作用，也即所谓的碰撞问题。要求解碰撞问题的第一步是对刚体碰撞进行检测，目前在物理引擎中注意是使用两阶段的检测方法。

1. Broad phase 初筛

   找到相交的 AABB

   可能的重叠的刚体对

2. Narrow phase

   精细地检测重叠

   生成碰撞信息

Broad Phase and Narrow Phase

Broad Phase

显然场景中大部分的物体是不会同时发生接触的，因此所谓的 broad phase 就是只利用物体的 bounding box 来快速筛选出可能发生碰撞的物体。目前物理引擎中常用的碰撞检测包括空间划分(space partitioning)以及 sort and sweep 两类方法。

BVH Tree

我们在介绍渲染技术时就介绍过空间划分的相关概念，它的思想是把场景中的物体使用一个树状的数据结构进行管理从而加速判断物体是否相交的过程。BVH 是空间划分的经典算法，它使用一棵二叉树来管理场景中所有物体的 bounding box。BVH 的特点是它可以通过动态更新节点来描述场景中物体的变化，因此可以快速地检测场景中的 bounding box 可能存在的碰撞。

Sort and Sweep

sort and sweep 是使用排序来检测碰撞的算法。它的思想非常直观：对于使用AABB 进行表示的 bounding box，两个 bounding box 出现碰撞时必然会导致它们的边界产生了重叠，而判断是否出现重叠则可以通过对 bounding box 的边界进行排序来进行计算。

对每个轴都要做

对第二个轴排序时，排序的数组是第一个轴中判断出的可能重叠的物体，这样会减少数量级

在物体移动的时候，只对局部进行移动

因为世界中大部分都是静态物体，所以第一次排好序之后，大部分物体的顺序就确定了

Narrow Phase – Objectives

筛选出可能发生碰撞的物体后就需要对它们进行实际的碰撞检测，这个阶段称为 narrow phase。除了进一步判断刚体是否相交外，在 narrow phase 中一般还需要去计算交点、相交深度以及方向等信息。

Narrow Phase – Approaches

相交方法：

Basic Shape Intersection Test

Minkowski Difference-based Methods

Separating Axis Theorem

Basic Shape Intersection Test

Minkowski Difference-based Methods

对于凸多边形的情况则可以使用 Minkowski差异(Minkowski distance) 来判断它们是否相交。在介绍 Minkowski 距离之前首先要引入 Minkowski 和 (Minkowski sum) 的概念：对于两个点集 $A$ 和 $B$，它们的 Minkowski 和定义为两个集合中任意一对矢量相加后得到的新的点集。

: { 1, 2 }

: { 1, 2, 3}

⊕ = { 1 + 1, 1 + 2, 1 + 3, 2 + 1, 2 + 2, 2 + 3 }

这里是去重之后的

物理意义：

1.物体上的所有点的集合 B ⊕ 某一点 A

⊕ = { + : ∈ , ∈ }

相当于 B 中沿着 OA 向量做了一个位移

2.物体上的所有点的集合 B ⊕ 某一条线 A

相当于 B 中沿着线 A 做了一个拖拽的范围

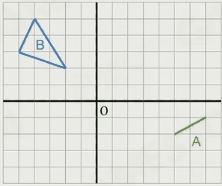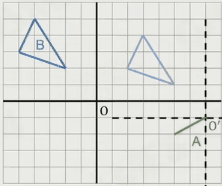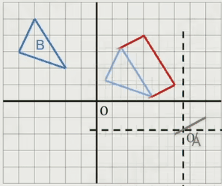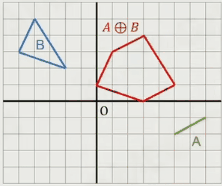
3.物体上的所有点的集合 B ⊕ 另一物体上的所有点的集合 A

相当于 B 沿着 A 的边线拖拽的范围

对于凸多边形，它们的Minkowski和也必为一个凸多边形，而且这个新多边形的顶点也是原始多边形顶点的和。

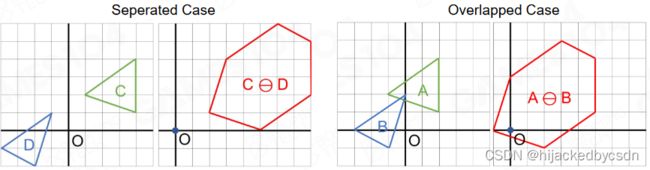
在此基础上我们定义点集 $A$ 和 $B$ 的 Minkowski 差异为 $A$ 和 $-B$ 的Minkowski和，即 $A\ominus B=A\oplus (-B)$。

⊖ = { − : ∈ , ∈ }

⊖ = ⊕ (−)

可以证明当 $A$ 和 $B$ 相交时，原点必位于 $A\ominus B$ 中。这样判断两个凸多边形是否相交的问题就转化为判断原点是否位于凸多边形 $A\ominus B$ 中的问题，这种问题一般可以使用 GJK 算法来求解。

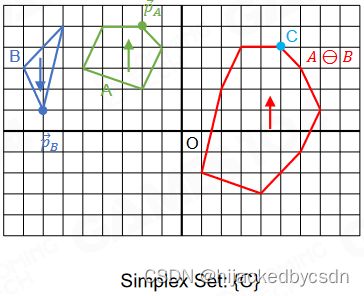
GJK Algorithm – Walkthrough

(Separation Case)

随便给一个方向

然后在一个形体 A 上找这个方向上最上方的顶点 $p_A$，另一个形体 B 上找这个方向上最下方的顶点 $p_B$

然后这两个顶点的减值点 C = $p_A\ominus p_B$ 一定在 $A\ominus B$ 上

连接原点 O 与点 C 得到 CO，取到 CO 的方向

检查原点是否在 simplex 中

嗯……这里没讲清楚这个 simplex 是啥

但是我猜应该是指的刚刚连接的这个 CO

然后之所以用 simplex 来指代，是因为之后会连更多线，形体会变得更复杂，就是会在 CO 的基础上增

Determine iteration direction
	If origin is in the simplex
		return true
	else
		Find nearest point to origin in the simplex
		If nearest distance reduced
			//continue iterating
		else
			return false
Find supporting points  and 
Add new point  −  to iteration simplex on Minkowski difference

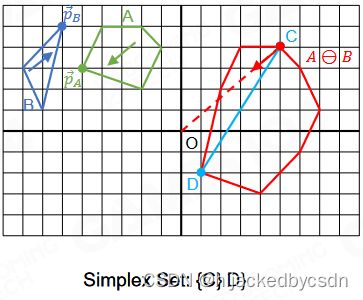
(Overlapped Case)

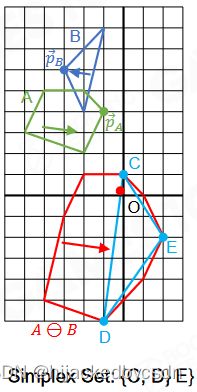
当GJK算法判断出两个凸多边形相交后还可以进一步计算交点以及深度等信息。

这里判断点在单纯形中其实就是化归为判断点在三角形中

GJK 有点朝着靠近的趋势迭代的意思

Separating Axis Theorem (SAT)

分离轴定理(separating axis theorem, SAT)同样是一种计算凸多边形相交的算法，它的思想是平面上任意两个互不相交的图形我们必然可以找到一条直线将它们分隔在两端。对于凸多边形还可以进一步证明必然存在以多边形顶点定义的直线来实现这样的分隔，因此判断凸多边形相交就等价于寻找这样的分隔直线。

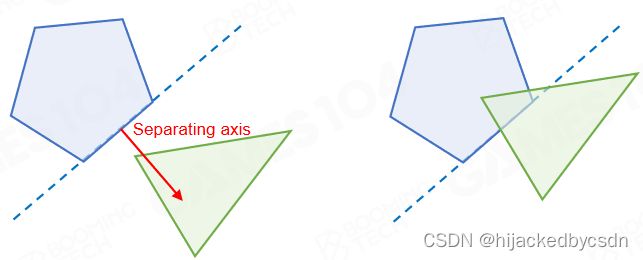
使用SAT判断凸多边形是否相交时需要分别对两个图形的边进行遍历，然后判断另一个图形上的每个顶点是否落在边的同一侧。只要发现存在一条边可以分隔两个图形即说明它们互不相交，否则继续遍历直到用尽所有的边，此时两个图形必然是相交的。

当图形的位置发生变化时还可以从上一次检测得到的分离轴开始重新进行检测，这样可以进一步提高算法的效率。

对于三维图形的情况则不仅需要考虑面和面的分隔关系，还要考虑边和边的分隔关系。

Collision Resolution

完成碰撞检测后就需要对发生碰撞的刚体进行处理，使它们相互分开。目前刚体的碰撞主要有三种处理思路，分别是 penalty force、velocity constraints 以及 position constraints，本节课我们主要介绍前两种处理方法。

Applying Penalty Force

penalty force 是最直观的碰撞处理方法，它的思想是当两个物体相交后沿反方向分别施加一个排斥力把它们推开。这种方法要求设置比较大的排斥力以及很小的积分时间间隔，否则容易出现非常不符合直觉的碰撞效果，因此现代物理引擎中几乎不会使用 penalty force 来处理刚体碰撞问题。

Solving Constraints

目前物理引擎中主流的刚体碰撞处理算法是基于Lagrangian力学的求解方法，它会把刚体之间的碰撞和接触转换为系统的约束，然后求解约束优化问题。

使用约束来表达世界

Non-penetration

Restitution

Friction

基本方法是给一个小小的连续的冲量，使用半隐式积分

Scene Query

除了上面介绍过的内容外，在游戏中我们往往还需要对场景中的物体进行一些查询，这些查询操作也需要物理引擎的支持。

Raycast

raycast 是非常基本的查询操作，我们希望能够获取某条射线在场景中击中的物体。实际上在光线追踪中就大量使用了 raycast 的相关操作，而在物理引擎中raycast也有大量的应用，比如说子弹击中目标就是使用 raycast 来实现的。

Mutiple hits 获取并返回所有 hit

Closest hit 获取所有 hit，返回最近的那个 hit

Any hit 获取任一个 hit 最快

Sweep

sweep 与 raycast 类似，不过在 sweep 中需要使用有一定几何形态的物体取击中场景中的其它物体。

Overlap

另一种常用的操作是 overlap，此时我们需要判断场景中的物体是否位于某个几何形状中。overlap 与碰撞检测非常类似，不过 overlap 一般只会使用简单的几何体来进行检测。像游戏中爆炸效果的检测就是使用 overlap 来实现的。

Collision Group

在物理引擎中还需要额外注意对场景中的物体进行分组，这样可以提高各种物理仿真算法的效率。

Efficiency, Accuracy, and Determinism

本节课最后讨论了物理仿真中的一些其它技巧。

Simulation Optimization

我们知道物理仿真是极其消耗计算资源的，如果在所有时刻都对场景中的物体进行模拟会造成计算资源的浪费。因此一种常用的手段是把场景中的物体划分为若干个island，当 island 内没有外力作用时就对它们进行休眠，这样就可以节约计算资源。

Continuous Collision Detection

当物体运动的速度过快时可能会出现一个物体之间穿过另一个物体的现象，此时可以使用 Continuous Collision Detection CCD 的相关方法来进行处理。

Deterministic Simulation

在进行物理仿真时还需要考虑仿真结果的确定性。尽管在编程时我们使用的都是同一套物理定律，在程序运行阶段由于帧率、计算顺序以及浮点数精度等问题容易出现同一个场景在不同终端上产生不同的模拟结果。

分离轴原理选择的边的顺序对结果有误差

如果要实现 Same old states + same inputs = same new states

还需要：

1. 相同步长的物理模拟

2. 确定性的物理模拟的求解顺序

3. 浮点精度的一致性

QA

物理模拟越逼真，就越能被称为好游戏吗

物理模拟不等于游戏性

游戏的物理、动画、渲染的 tick 速度是一样的吗

经典的 动画和渲染的 tick 差不多，物理和逻辑的 tick 差不多

但是也有一种想法是，物理和动画的 tick 可以减慢

可以用 GPU 做物理计算

可以的

网络游戏物理计算是放在服务器上吗

一般的物理计算不会参与逻辑的，物理只是为了表现

有些游戏会尝试把物理放服务端，但是这里会有一个服务器向客户端同步

之前讲过，如果物理模拟是确定的，就可以尝试用帧同步来同步物理

第十一节 物理系统：高级应用

Character Controller

角色控制器(character controller)是玩家操作角色和游戏世界进行交互的接口。和很多人直观的认识不同，角色控制器在很多情况下实际上是一个非物理的。最常见的例子是玩家控制角色停止移动时角色会立即停住，而不是严格按照刚体仿真那样通过摩擦力来逐渐停止运动。某种意义上讲，角色控制器虽然是反物理的但却更符合人对物理世界的认知。

Build a Controller in Physics System

在构建角色控制器时一般会使用简化后的形状来包裹角色，这样便于处理各种场景之间的互动。

胶囊体外面可以再套一层，防止距离其他物体太近，防止距离墙太近，也可以防止摄像机穿透墙壁，看到墙壁之后的东西

Collide with Environment

在角色和场景进行互动时最常见的情况是玩家控制的角色撞到了墙壁上。如果严格按照物理引擎进行模拟，此时角色会一直停在碰撞的位置；而现代游戏中更常见的处理方式是修改角色的运动方向，使得角色可以沿墙壁方向进行滑动。

Auto Stepping

上下楼梯同样也是角色在场景中的一种常见行为。如果严格按照物理仿真进行处理，胶囊的上下楼梯会非常地困难。因此在游戏引擎中需要单独考虑这种情况，当角色上下楼梯时自动修正角色的位置。

具体做法是，每一帧移动角色的时候都会尝试把角色往高抬一点点

Slope Limits and Force Sliding Down

对于斜坡这种情况，如果按照刚体运动学进行处理会导致角色下坡时直接从斜坡上滑下来，或是在上坡时由于具有过大的速度角色直接冲上它不应该到达的位置。为了避免这些问题需要单独考虑角色停在斜坡或是限制角色的位置。

Controller Volume Update

角色控制器还需要考虑角色体积发生变化的情况。当玩家控制角色进行下蹲等动作时需要自动更新角色控制体的体积，否则容易出现角色卡在门口无法进入的问题。

Controller Push Objects

当玩家控制角色和场景中的物体互动时需要对动态对象的运动状态加以更新。比较常见的处理方式是发生碰撞时对动态对象施加一个相应的冲量来控制它们的运动。

Standing on Moving Platform

除此之外，角色控制器还需要考虑动态场景的情况。当角色位于运动的平台时需要根据平台的运动来调整角色的运动状态，否则会出现平台发生运动时角色的运动没有同步或是滞后的问题。

简单的 hack 是直接将平台与角色绑定

如果要做那种更复杂的，平台的加速度会影响到角色，让角色失衡之类的，那就需要专门研究了

Ragdoll

布娃娃(ragdoll)系统是游戏角色动画的一个重要组成部分，它最常见的例子是角色的处决动画：当玩家控制的角色处决了某个游戏对象时，根据处决场景的不同被处决对象会发生相应场景互动的动作。

Map Skeleton to Rigid Bodies

实际上ragdoll与前面介绍过的骨骼动画密切相关。在模拟ragdoll的运动时，我们同样会在角色身上设置相应的节点并把不同节点之间的骨骼按照刚体进行模拟。不过出于实时计算上的考虑，ragdoll 一般只会使用非常少量的节点和骨骼来进行模拟。

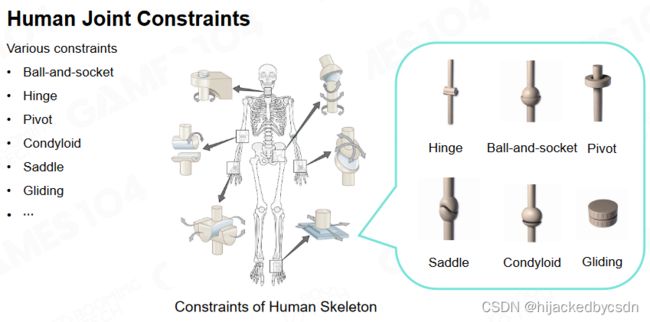
Human Joint Constraints

同样地，在 ragdoll 中需要考虑角色身上不同节点的运动是带有一定约束的。如果忽略了人体骨骼关节的约束则会导致非常扭曲的模拟效果。

一般来说 ragdoll 关节的约束会由 TA 进行设置，如果设置的不好会出现一些反直觉的动画效果。

Animating Skeleton by Ragdoll

需要注意的是尽管我们可以使用 ragdoll 来模拟角色的动画，在实际游戏中仍然是需要通过骨骼关节系统来驱动整个角色的运动。由于 ragdoll 中的骨骼关节数量一般会少于实际角色的骨骼关节，我们需要使用动画重定向技术来将 ragdoll 计算出的运动映射到实际的角色骨骼上。

Leaf joints 是 Ragdoll 覆盖不到的部分，这部分就直接使用 Animation 控制

Active joints 是 Ragdoll 物理控制的部分

Intermediate joints 是中间的部分，是前后两个 Ragdoll Joint 插值得到的

Blending between Animation and Ragdoll

在使用时还需要注意角色动画切换到 ragdoll 的过程。还是以角色处决动画为例，在一开始被处决对象是使用预先录制的角色动画，然后在某一时刻会切换成 ragdoll 使用物理系统来实时计算角色的行为。

更进一步，在现代3A游戏中还会将角色动画和ragdoll实时计算出的动画进行混合来提升玩家的代入感和游戏体验。

Cloth

布料系统是游戏物理仿真中的重要一环。早期的布料模拟是使用预先录制的动画来实现的，我们可以在角色身上设置一些额外的骨骼来控制衣物的运动，这样就可以实现角色执行不同动作时衣物随之飘动的效果。

另一种处理衣物的方法是使用刚体运动的方法来模拟衣物和角色以及场景的互动。这样的处理方法虽然需要更多的计算资源，但可以实现相对真实衣物运动的效果。

Mesh-Based Cloth Simulation

而在现代游戏引擎中衣物运动更多地是使用网格来进行模拟。这里首先要说明的是布料仿真中使用的网格是不同于渲染中所使用的网格，出于计算效率上的考虑布料仿真中使用的网格要比渲染中的网格要稀疏很多。

同时在布料仿真中往往还会为网格上的每个顶点赋予一定位移的约束，从而获得更符合人直觉的仿真结果。

越靠近肢体的地方约束的权重越高

Mass-Spring System

使用网格进行布料仿真的基本处理方法是使用质点弹簧系统进行模拟。我们为网格的顶点赋予一定的质量，然后将相邻顶点使用弹簧连接起来就形成了布料仿真的物理系统。这里需要注意的是除了弹簧弹力之外一般还需要为质点施加一定的阻尼来保证质点的运动最终能够停住。

在放置弹簧时除了横竖方向外一般还需要在对角方向上也设置一些弹簧，这样可以保证布料具有抵抗对角方向的刚度。

101 这里还讲到了要在跳点之间加弹簧，抵抗非平面力

最后把外力施加在质点弹簧系统上就可以进行布料的运动仿真了。这里需要注意的是在进行仿真时不要忘记质点除了弹簧施加的弹力和阻尼外自身还会收到重力以及空气阻力的作用。

Verlet Integration

对质点弹簧系统进行仿真时不可避免地会使用到一些数值积分的方法，这里我们着重介绍一些Verlet积分算法。Verlet积分本质仍然是半隐式欧拉积分，不过在实际积分时可以将速度项约掉只保留位移和加速度项就能进行计算。因此Verlet积分不需要保存每一时刻的速度，我们只需要位移和力(加速度)就可以进行计算，从而提高布料仿真的效率。

( + Δ) = () + () ∆

( + Δ) = () + ( + Δ) ∆

() = ( − Δ) + () ∆

将 ( + Δ) 代入 ( + Δ) =>

( + Δ) = () + ( () + () ∆)∆

() = ( − Δ) + () ∆

将 () ∆ 代入 ( + Δ) =>

( + ∆) = 2 () − ( − ∆) + () (∆)^2

消去速度的优点在于，速度可能会突变，不稳定

Cloth Solver – Position Based Dynamics

Constrains -> Force -> Velocity -> Position

PBD: Constrains -> Position

Self Collision

布料仿真的一大难点在于如何处理自相交(self collision)问题。由于我们使用了没有体积的网格来表示布料，在进行仿真时很容易出现网格直接相互的穿插。

目前布料自相交的问题还没有一个十分完善的解决方法。在工业界会使用一些trick来缓解自相交的问题，比如说对布料进行加厚、减少仿真时的时间步长、限制顶点的速度以及使用SDF进行控制等。

具体做法有：

将布料调厚

在一个物理步中使用多个子步

钳制最大速度

引入接触约束，摩擦约束

在布料内部有一个斥力场

等等

Destruction

玩家对场景的破坏是通过破坏系统来进行实现。一个好的破坏系统可以极大地提升玩家的游戏体验，有些游戏甚至是以破坏系统为核心玩法进行设计的。

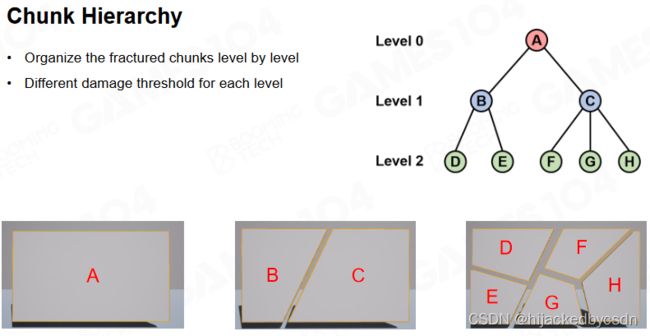
Chunk Hierarchy

我们可以使用一棵树来描述同一物体不同碎片之间的层次关系：树的根节点表示完整的物体，而它下面的每一层表示物体经受一定程度的冲击后所产生的碎片。

Connectivity Graph

当确定了物体承受的冲击后就可以使用一张图来表示不同碎片之间的连接关系：图的节点表示碎片，而图的边则表示相互连接的碎片能够承受的荷载，当冲击大于边上的值时就会发生物体的破碎。

Damage Calculation

需要说明的是虽然我们使用了冲击和荷载这样的字眼，实际上在游戏引擎中却不会去计算这些物理量。它们只是一些人工设置的数值，并不具备真实的物理意义。在游戏开发中一般会使用一些经验公式来对冲击以及物体的承载力进行计算。

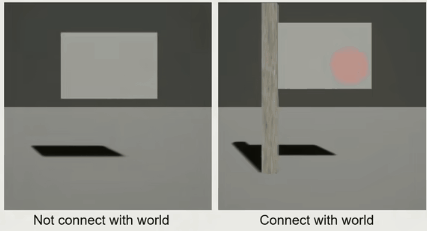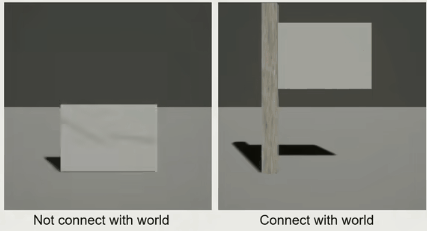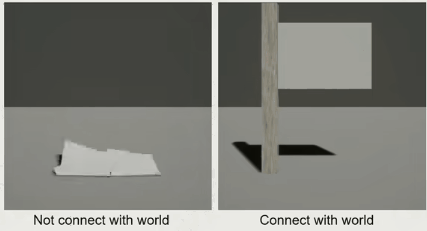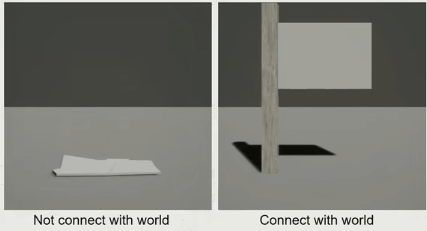
Destruction with/without Support Graph

有了 Support Graph，得到的效果就是，可以支持部分破坏

因为我们是提前计算好的全部断裂是怎么样的，所以需要支持仅部分破坏

Build Chunks by Voronoi Diagram

那么如何去生成这样的一张图呢？在物理引擎中一般会使用Voronoi图(Voronoi diagram)这样的技术来对原始的物体区域进行划分，划分后的每一个区域即为所需的碎片。

对于三维的情况则要更加复杂一些，除了需要使用 Voronoi 图对空间进行划分还需要使用 Delaunay 三角化来重新生成碎片的三维网格。同时当物体破碎后还需要为碎片的网格赋予内部材质的纹理，这一般需要使用一些程序化的纹理生成算法。

也可以离线生成断面纹理

一般不会让破碎物体参与逻辑，也是因为同步难

在设置Voronoi图的种子时还可以根据需要设置不同模式的种子，这样可以实现相应的破碎效果。

Destruction in Physics System

从物理系统的计算流程上来看，破碎系统一般是仿真碰撞检测后实际解算之前。这主要是因为很多破碎的事件是由碰撞所导致的，同时在物体破碎后往往还会产生新的物体(碎片)需要计算相应的运动。

Issues with Destruction

破坏的碎片也要提供回调函数，用于表现

例如声音，粒子特效，导航网格更新之类的

破坏系统的计算是相当昂贵的：当一个物体出现破碎后往往会带来成百上千个碎片需要进行物理仿真，这会极大地增加物理系统的计算负载，因此在使用时需要慎重考虑。

Popular Destruction Implementations

NVIDIA APEX Destruction

NVIDIA Blast

Havok Destruction

Chaos Destruction(Epic Games.)

Vehicle

载具系统是现代游戏中重要的组成部分。要对载具进行模拟需要推导相应的动力学模型，以汽车为例整个汽车可以看做通过悬挂系统与地面接触的刚体。

Vehicle Mechanism Modeling

车身

弹簧

轮子

Traction Force

汽车引擎输出扭矩，而扭矩的大小则需要查询引擎的相关曲线来计算。

差速器在检测到有些轮子悬空有些轮子抓地，就会把更多扭矩分配到抓地的轮子上，让汽车脱困

Suspension Force

在竖直方向上由于地面的起伏车身会产生悬挂系统所导致的振动。

Tire Forces

在平面上汽车的轮胎会产生平行于前进方向的径向力，同时还会产生的切向力控制车辆的转动。

我不知道这里的 tateral force 是不是所谓的切向力，反正这个 tateral force 应该是老师讲的，轮子转动产生的滑动摩擦力

这个滑动摩擦力与压力有关系，所以也就和汽车重心有关系，因为重心位置决定了轮子受到的压力

打滑就是因为滑动摩擦力有上限

Center of Mass

根据车身重量的分布我们还需要计算汽车的重心。实际上重心的位置不仅会控制汽车的振动，还会汽车的转向性能有重要的影响。

一般是重心偏后的话，车子从空中落地的话不容易翻

一般的车都是前轮既当驱动轮又当转向轮。所以如果重心靠前的话，转动惯量就不租，转向就比较弱

同时需要注意的是当车辆进行加速或是刹车时重心的位置也会发生一些变化。比如加速的时候车身后仰

为了更好地实现转向，现代汽车在设计时会让两个转向轮的转动有微小的差异。在进行模拟时也需要考虑这个微小的角度变化。

如果两轮转动角相同的话，外轮是空转的

这就是考虑到车是一个刚体，两轮是有距离的

最后需要说明的是在计算地面和车轮求交时需要把轮子看做是球，这样才能模拟出车辆在凹凸不平的地面上行驶的效果。

Advanced: PBD/XPBD

PBD

本节课最后讨论了 PBD 和 XPBD 两种更高级的物理仿真技术。和前面介绍过的仿真技术相比，PBD 和 XPBD 是建立在拉格朗日力学(Lagrangian mechanics)基础上的仿真方法。在拉格朗日力学的框架中不再考虑力等物理概念，而是把物理定律视为系统的某种约束来描述运动。

1. Collision constriaints 碰撞约束

   1. Non-penetration 不相交

   2. Friction 摩擦力

   3. Restitution 恢复力

2. Cloth constraints 布料模拟

   1. Stretching 拉伸

   2. Bending 弯曲

Circling Constraint

以匀速圆周运动为例，在拉格朗日力学中我们不会去计算各种改变质点运动状态的力，而是考虑质点运动的位置约束以及速度约束。其中位置约束的导数也称为 Jacobian 矩阵。

String Constraints

类似地，弹簧质点系统也可以表示为由约束定义的系统。

PBD – Constraints Projection

PBD 在求解时，PBD 会把整个物理系统描述为关于位置的约束，然后就能得到雅可比矩阵，也就是知道倾向性是什么，也就知道了，在一个步长之下，每一个变量的扰动的趋势是什么。然后通过不断迭代来计算满足约束的解。

这里对 $C(X^{(k{)}^{\prime }}+\Delta X)$ 做了泰勒展开

传统的位置和速度这种可能产生不稳定的因素就没有了

$\lambda$ 相当于步长，而 $\Delta X$ 的方向由雅可比矩阵的切线方向决定

Position Based Dynamics – Workflow

在每一个时刻都会执行一遍 loop，所以 loop 内是一个 time step

一开始做半隐式积分

然后判断是否有相交，有相交就生成约束，然后迭代约束

然后把根据约束求出来的位置和速度赋回去

最后给速度加上摩擦阻尼

PBD 是目前游戏行业非常热门的物理仿真技术，和传统仿真技术相比 PBD 往往会得到更稳定的解。

XPBD

XPBD 可以看做是对PBD的一种推广，它在 PBD 的基础上引入了刚度(stiffness)的概念来描述不同约束的强弱。

中间 alpha 是硬度

$U(x)=\frac{1}{2}C(X{)}^T{\alpha }^{-1}C(X)$

类比到 $\frac{1}{2}{k}^{2}x$

有一种表达了刚度的感觉

参考资料

Character Controller & Ragdoll

• Character Controllers Chapter in PhysX User’s Guide:
https://docs.nvidia.com/gameworks/content/gameworkslibrary/physx/guide/Manual/CharacterController
s.html
• Diablo 3 Ragdolls: How to smack a demon, Erin Catto, GDC 2012:
https://box2d.org/files/ErinCatto_Ragdolls_GDC2012.pdf
• Physics Animation in ‘Uncharted 4: A Thief’s End’, Michal Mach, Naughty Dog, GDC 2017:
https://gdcvault.com/play/1024087/Physics-Animation-in-Uncharted-4
• Physics Driven Ragdolls and Animation at EA: From Sports to Star Wars, Jalpesh Sachania, Frostbite
EA, GDC 2018: https://gdcvault.com/play/1025210/Physics-Driven-Ragdolls-and-Animation
• Physical Animation in ‘Star Wars Jedi: Fallen Order’, Bartlomiej Waszak, Respawn Entertainment,
GDC Summit 2020: https://gdcvault.com/play/1026848/Physical-Animation-in-Star-Wars

Clothing

• Blowing from the West: Simulating Wind in ‘Ghost of Tsushima’, Bill Rockenbeck, Sucker Punch
Productions, GDC 2021: https://www.gdcvault.com/play/1027124/Blowing-from-the-West-Simulating
• Cloth Self Collision with Predictive Contacts, Chris Lewin, Electronic Arts, GDC 2018:
https://www.gdcvault.com/play/1025083/Cloth-Self-Collision-with-Predictive
• Machine Learning: Physics Simulation, Kolmogorov Complexity, and Squishy Bunnies, Daniel Holden,
Ubisoft Montreal, GDC 2020: https://www.gdcvault.com/play/1026713/Machine-Learning-Physics-
Simulation-Kolmogorov
• Matt’s Webcorner - Cloth - Stanford Computer Graphics, Stanford 2014 Course,
https://graphics.stanford.edu/~mdfisher/cloth.html
• 从零开始学图形学：弹簧质点系统——Euler Method和Verlet Integration, 启思, 知乎专栏
https://zhuanlan.zhihu.com/p/355170943

Destruction

• 游戏破坏系统简介，网易游戏雷火事业群，知乎 https://zhuanlan.zhihu.com/p/346846195
• Destructible Environments in ‘Control’: Lessons in Procedural Destruction, Johannes Richter, Remedy,
GDC Summer 2020, https://www.gdcvault.com/play/1026820/Destructible-Environments-in-Control-
Lessons
• The Art of Destruction in ‘Rainbow Six: Siege’, Julien L’Heureux, Ubisoft, GDC 2016,
https://www.gdcvault.com/play/1023307/The-Art-of-Destruction-in
• NVIDIA Blast official site, https://developer.nvidia.com/blast
• Voronoi Diagram, https://cs.brown.edu/courses/cs252/misc/resources/lectures/pdf/notes09.pdf
• Delaunay Triangulations,
https://members.loria.fr/monique.teillaud/collab/Astonishing/2017_workshop_slides/Olivier_Devillers.pdf
• Unreal Engine Chaos, https://docs.unrealengine.com/4.27/en-
US/InteractiveExperiences/Physics/ChaosPhysics/Overview/

Vehicle

• Vehicle Chapter in PhysX User’s Guide:
https://docs.nvidia.com/gameworks/content/gameworkslibrary/physx/guide/Manual/CharacterController
s.html
• Vehicle in Unreal Engine User’s Guide: https://docs.unrealengine.com/4.27/en-
US/InteractiveExperiences/Vehicles/VehicleUserGuide/
• Car Physics for Games, Marco Monster:
https://asawicki.info/Mirror/Car%20Physics%20for%20Games/Car%20Physics%20for%20Games.html
• Replicating Chaos: Vehicle Replication in Watch Dogs 2, Matt Delbosc, Ubisoft Toronto, GDC 2017:
https://www.gdcvault.com/play/1026956/Replicating-Chaos-Vehicle-Replication-in

PBD

• Positon Based Dynamics, M. Müller et al., 3rd Workshop in Virtual Reality Interactions and Physical
Simulation "VRIPHYS“, 2006: https://matthias-research.github.io/pages/publications/posBasedDyn.pdf
• XPBD: Position-Based Simulation of Compliant Constrained Dynamics, M. Macklin et al., MIG '16:
Proceedings of the 9th International Conference on Motion in Games, 2016:
http://mmacklin.com/xpbd.pdf
• Detailed Rigid Body Simulation using Extended Position Based Dynamics, M. Müller et al., Symposium
on Computer Animation, 2020:
https://www.researchgate.net/publication/344464310_Detailed_Rigid_Body_Simulation_using_Extende
d_Position_Based_Dynamics
• Position Based Dynamics: A fast yet physically plausible method for deformable body simulation,
Tiantian Liu, GAMES Webinar 2019-88: https://slides.games-
cn.org/pdf/Games201988%E5%88%98%E5%A4%A9%E6%B7%BB.pdf