过拟合、欠拟合的通俗理解!过拟合和欠拟合的解决办法,以及dropout和正则化的讲解,代码实现(对于mnist数据集)!
这里写目录标题
- 一 、过拟合、欠拟合的通俗理解
- 二、欠拟合和过拟合的解决办法
-
- 一、欠拟合
- 二、过拟合
-
- 一 、在网络深度中加入dropout()层次
- 二、正则化
-
- 一、L2正则化:
- 三、图像增强
- 三、搭建模型的参数的选择
-
- 一、首先开发一个过拟合模型
- 二、抑制过拟合
- 三 、参数选择
- 四、代码证明(dropout)
一 、过拟合、欠拟合的通俗理解
一味追求提高对训练数据的预测能力,所选模型的复杂度则 往往会比真模型更高。这种现象称为过拟合(over-fitting)。过拟合 是指学习时选择的模型所包含的参数过多,以致于出现这一模型对已 知数据预测得很好,但对未知数据预测得很差的现象。可以说模型选 择旨在避免过拟合并提高模型的预测能力。欠拟合,就是拟合过低。
这个是书面语言,听得云里雾里,来看看我们怎么通俗理解!
过拟合:在训练集上测试正确度较高,在测试集上测试正确度较低。
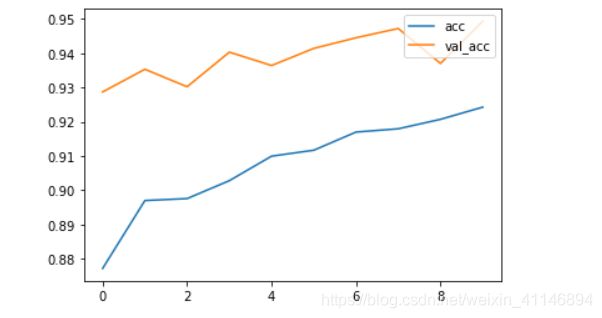
下面这两张图都是过拟合的图片,当训练集和测试集的正确率趋于稳定的时候,此时测试集的正确率低于训练集的正确率,这就叫过拟合。在这里(val_acc:测试集的正确率,acc:训练集的正确率)
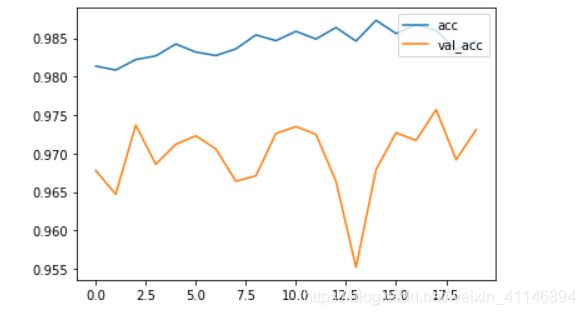
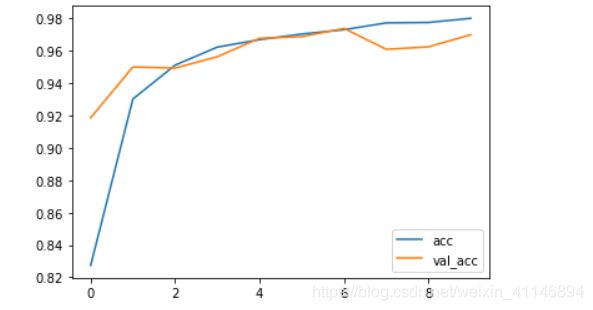
欠拟合:训练集正确度比较低,在测试集上测试正确度较低。
这里比较低是随着训练,测试集和训练集正确度不再增加。
在深度学习里面,欠拟合一般不是问题,过拟合才可能使我们遇到的大问题。
二、欠拟合和过拟合的解决办法
一、欠拟合
增加网络深度和隐藏层的单元数。
二、过拟合
抑制过拟合的方法一般有:在网络中添加Dropout层,正则化,图像增强,其实最好的是增加数据集。
一 、在网络深度中加入dropout()层次
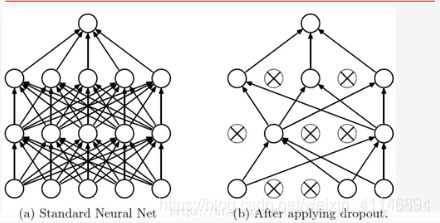
为什么说dropout层可以解决过拟合:


其实说到底就是,每次训练的时候dropout会随机删除掉一些单元,不去训练,那么这就相当于训练了很多模型在里面,然后共用这些模型去评测,求平均模型,可以有效的防止过拟合,感觉和adaboost有点像,把多个弱分类器组合成一个强分类器。如果还是不是很懂,你想一下嘛,一个人做决策,是不是容易造成独裁,和大家投票表决,采取大多数人的意见,哪个会让老百姓的我们更加满意?
二、正则化
正则化分为两种,一种是L1正则化,一种是L2正则化。
这里只介绍L2正则化,两者之间都是大同小异,需要了解L1正则化的同学,可以看看其他博客。
一、L2正则化:
我们首先来看一下一张图:
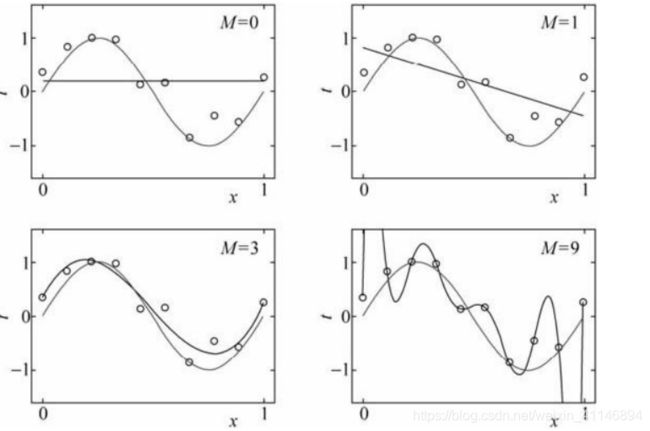
这里很容易知道图四是过拟合,训练集的正确率非常高,图一,图二是欠拟合。
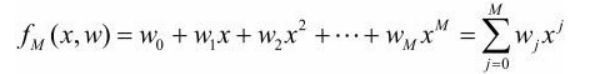
上面的M代表是多项式的次数,M=9,代表的是9次多项式。这里很容易知道,如果要防止过拟合,就需要把9次多项式,变为3次多项式。那么怎么变成了?这个就需要看他的损失函数了,L2正则化主要是在损失函数后面加了一个对应权重的求和:
L = L 0 + λ 2 n ∑ i n w i 2 L={{L}_{0}}+\frac{\lambda }{2n}\sum\limits_{i}^{n}{w_{i}^{2}} L=L0+2nλi∑nwi2
对其求偏导可知:
∂ L ∂ w i = ∂ L 0 ∂ w + 1 n w i ∂ L ∂ b = ∂ L 0 ∂ b \frac{{\partial L}}{{\partial {w_i}}} = \frac{{\partial {L_0}}}{{\partial w}} + \frac{1}{n}{w_i}\\ \frac{{\partial L}}{{\partial b}} = \frac{{\partial {L_0}}}{{\partial b}} ∂wi∂L=∂w∂L0+n1wi∂b∂L=∂b∂L0
最后更新的权重变为:
w i = w i − η ( ∂ L 0 ∂ w + λ n w i ) = ( 1 − λ n ) w i − η ∂ L 0 ∂ w b = b − η ∂ L 0 ∂ b {w_i} = {w_i} - \eta (\frac{{\partial {L_0}}}{{\partial w}} + \frac{\lambda }{n}{w_i}) = (1 - \frac{\lambda }{n})w_i - \eta \frac{{\partial {L_0}}}{{\partial w}}\\ b = b - \eta \frac{{\partial {L_0}}}{{\partial b}} wi=wi−η(∂w∂L0+nλwi)=(1−nλ)wi−η∂w∂L0b=b−η∂b∂L0
如果损失函数没有加最后的权重平方求和的话,对应权重更新就会是:
w i = w i − η ∂ L 0 ∂ w b = b − η ∂ L 0 ∂ b {w_i} = {w_i} - \eta \frac{{\partial {L_0}}}{{\partial w}}\\ b = b - \eta \frac{{\partial {L_0}}}{{\partial b}} wi=wi−η∂w∂L0b=b−η∂b∂L0
其中的n,λ,η都是正数。两者对比后你会发现加了权重之后的权重更新会更加小,权重跟新就只有(1− n/λ)wi 和wi之间有区别,同样的条件下,(1− n/λ)wi会更加小。这样就会让一些不是很重要的权重,最后接近于0,那么对应于fm(x)的影响就不是很大,最后拟合的图就会回到图三那样。
这里对于λ的大小可以这样来理解:
λ越大,越倾向于以追求小权重为主要目标
λ越大,越倾向于以最小化原始损失函数为主要目标。
三、图像增强
比如说直方图那些,这方面说起来就不说了,具体的可以看看其他资料。
三、搭建模型的参数的选择
一、首先开发一个过拟合模型
(1)、添加更多的层
(2)、让每一层变得更大
(3)、训练更多的轮次
二、抑制过拟合
(1)、dropout()
(2)、正则化
(3)、图像增强
(4)、增加训练数据
三 、参数选择
再次调节超参数:
(1)、学习速率
(2)、隐藏层的单元数
(4)、训练轮次
构建网络的总原则:保证神经网络容量做够拟合数据
四、代码证明(dropout)
这里是自己搭建了两个全连接网络,也就是Bp神经网络,数据集是来源于mnist数据集。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#mnist数据
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
#m创建模型
input = tf.keras.Input(shape=(28,28))
x = tf.keras.layers.Flatten()(input )
x = tf.keras.layers.Dense(784,activation='relu')(x)
x = tf.keras.layers.Dropout(0.3)(x)
output = tf.keras.layers.Dense(10,activation='softmax')(x)
model = tf.keras.Model(inputs=[input],outputs=[output])
#m设置优化参数
model.compile(optimizer='adam', loss = 'sparse_categorical_crossentropy' , metrics = ['acc'])
#m数据填充
history=model.fit(x_train,y_train,epochs=10,validation_data=[x_test,y_test])
p1 = plt.plot(history.epoch,history.history['acc'],color='red')
p2 = plt.plot(history.epoch,history.history['val_acc'])
plt.legend([p1,p2],['acc','val_acc'],loc='lower right', scatterpoints=1)
没加dropout层,很明显发生了过拟合,val_acc是测试集的正确率,acc是训练集的正确率,很明显,这里发生了过拟合:
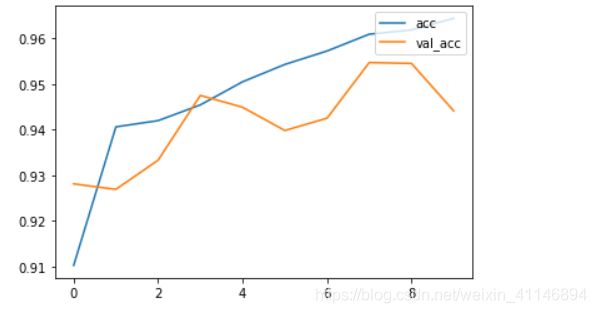
加了dropout层后,防止了过拟合: