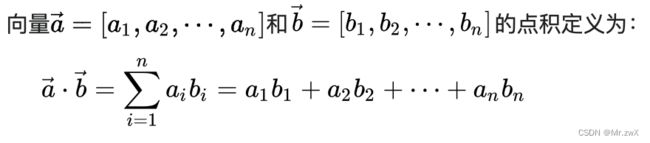【关于乘法这些事儿】概念和代码的区分

接触数学和神经网络这么久了，始终还是分不清几种乘法（捂脸）和对应代码，最近组里讲到“内积外积优化神经网络在硬件上的访存”的论文（SpArch: Efficient Architecture for Sparse Matrix Multiplication [HPCA’20]），借此机会来理一理乘法这些事儿。

---

1 内积（inner product）/点积（dot product）/数量或标量积（scalar product）

a 概念

维度：[1, m] and [1, m] => 1；或写成[1, m]和[m, 1]的矩阵乘法 => 1
最终结果是一个标量。

代数定义

这种运算方式得到的结果是一个标量。由此可见，内积和矩阵乘法中每个输出值的计算方式一致。

b 代码

torch.dot()  # for two 1D tensor

参考：Wikipedia - Dot product

2 矩阵乘（matrix multiplication）/矩阵积（matrix product）

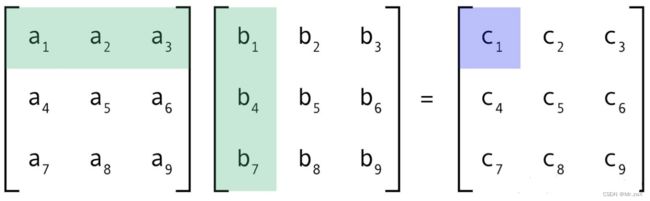
a 概念

维度：[m, n] and [n, k] => [m, k]
这是我们最最最熟悉的矩阵操作，标准矩阵乘法。以下也是最常见的 基于内积的矩阵乘（敲重点） 计算方式。注意，每个输出元素都是一个标量，最终结果是一个矩阵。

代数定义

b 代码

torch.mm()  # no broadcast
torch.matmul()  # have broadcast
torch.bmm()  # no broadcast, support batch matmul
@  # the same with bmm

参考：Wikipedia - Matrix multiplication

3 外积（outer product）/张量积（tensor product）

a 概念

维度：[m, 1] and [n, 1] => [m, n]
最终结果是一个矩阵。

注意，张量积是外积的一种扩展。

外积就是行向量和列向量的乘法。

b 代码

torch.outer()

参考：Wikipedia - Outer product, Wikipedia - Tensor product

！及时补充：基于外积的矩阵乘！

维度：[m, n] and [n, k] => [n, m, k] => 在n维度上求和 => [m, k]
除了最常见的 基于内积的矩阵乘，还有一种 基于外积的矩阵乘。
矩阵乘其实可以看成多个向量外积之和！
如下图，可以用A的每一列和B的每一行求外积，得到多个输出矩阵，最后叠加在一起得到矩阵乘的结果。

对比：基于内积的矩阵乘 VS. 基于外积的矩阵乘

前者：输入矩阵的复用性很差，需要反复存取；而输出矩阵复用性很高，只需要一个矩阵的存
后者：输入矩阵的复用性很好，用D的每一列去和E的对应行做外积，得到多个输出矩阵

参考：SpArch: Efficient Architecture for Sparse Matrix Multiplication (HPCA 2020)

4 哈达玛积（hadamard product）/逐点乘积（element-wise product）/分素乘积（entrywise product）

a 概念

维度：[m, n] and [m, n] => [m, n]
最终结果是一个矩阵，

b 代码

torch.mul()
torch.multiply()  # alias for torch.mul

5 外积（cross product）/叉积或叉乘/矢量积或向量积（vector product）

a 概念

前面讲了内积的结果是一个标量，而叉乘的结果则是一个向量。这个在神经网络中不常用。
叉乘仅定义在三维欧氏空间，需要用到 右手定则，我们这里的cross product翻译成外积其实很容易和上文的张量积混淆！！！叉乘一般不说外积！

代数定义

b 代码

torch.cross()

注意，网上有人说叉乘是传统矩阵乘，用matmul，这个是有问题的！

6 神经网络常用运算：卷积

a 概念

这个在卷积神经网络中就广泛应用了，通过滑动窗口实现参数复用。每个窗口内对应位置相乘最后全部相加。
（窗口内是什么操作？比较像内积，但是内积是针对的1D向量。可以称为“局部点积”？知道的小伙伴可以告诉我）

b 代码

torch.nn.Conv2d()  # 给input的同时，指定kernel的W和b
torch.nn.functional.conv2d()  # 直接给input 

参考资料

• Wikipedia Document
• 矩阵乘法核心思想（5）：内积与外积
• 点积、内积、外积、叉积、张量积——概念区分
• PyTorch/Docs