数学建模之拟合

1 拟合法概述

与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好（最小化损失函数）

一个小例子

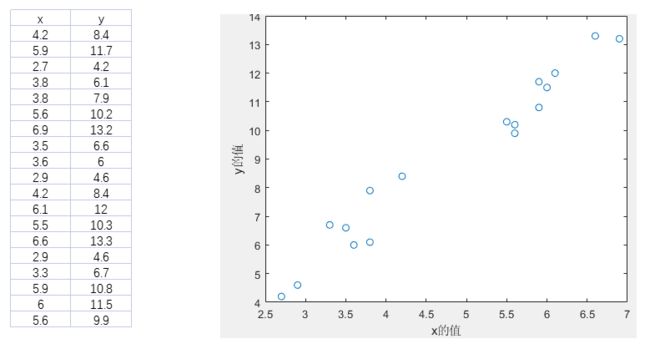
已有文件 data1.xlsx 保存了 x、y 的值，使用 Matlab 画图如下：

❗️注意：

• 将数据导入到 Matlab 时，我们是分别创建了两个变量：x 和 y，每个变量仅保存一列数据，并将变量保存到了 data1.mat 文件中

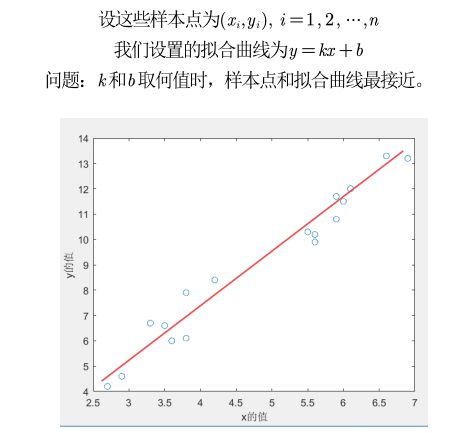
那么接下来，我们如何 确定拟合曲线 呢？

• 将样本送入Matlab 中画图

2 最小二乘法

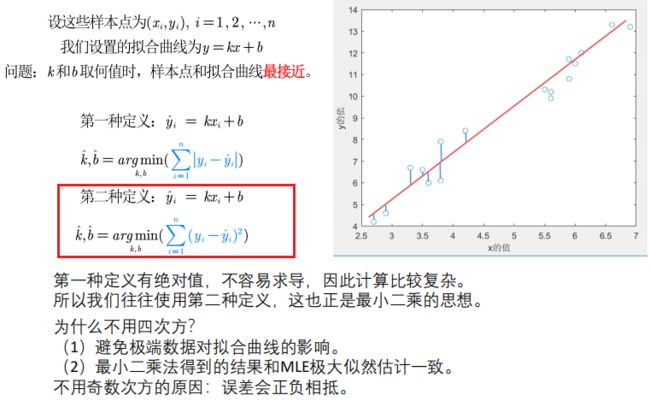
2.1 最小二乘几何解释

2.2 最小二乘求解

使用 Matlab 求解最小二乘

3 算法评价

拟合完成后，我们如何评价拟合的好坏呢？

如何判断线性于参数的函数？

• 在函数中，参数仅以一次方出现，且不能乘以或除以其他任何的参数，并不
  能出现参数的复合函数形式。

❗️注意：

• 虽然多元函数拟合的效果可能要比一元函数要好，但是我们的拟合函数要尽可能选择简单的。比如极端情况就用多项式插值，SSE显然是为0的，但是这就和我们使用拟合的初衷相矛盾了

使用 Matlab 计算拟合优度

4 代码编写

利用最小二乘法求得 k、b

clear;clc
load  data1
plot(x,y,'o')
% 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线

% 画出y=kx+b的函数图像 plot(x,y)
% 方法一：传统的画法：模拟生成x和y的序列，比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7  % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b  % k和b都是已知值
% plot(xx,yy,'-')

% 方法二：匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数，可以是一个，也可以是多个，用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
%  z=@(x,y) x^2+y^2; 
%  z(1,2) 
% % ans =  5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval =  [xmin xmax] 表示定义域的范围
f=@(x) k*x+b;
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','SouthEast')

计算拟合优度

y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2)  % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR   % 5.6843e-14  =   5.6843*10^-14   matlab浮点数计算的一个误差
R_2 = SSR / SST

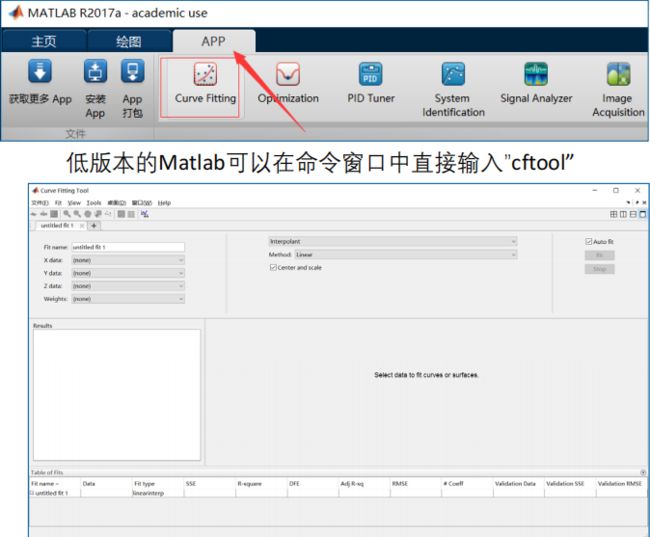
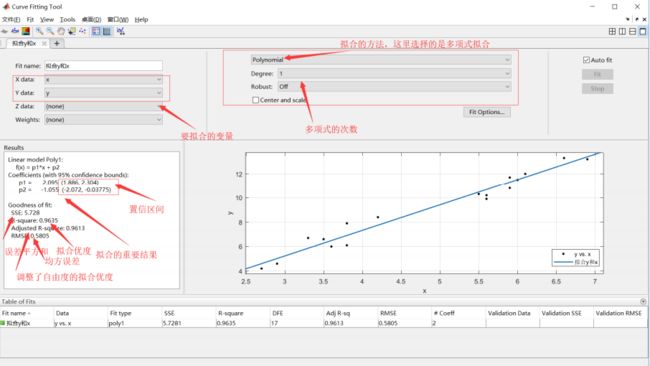
5 曲线拟合器

这里使用曲线拟合器得到的结果和我们之前使用代码实现的结果是一样的

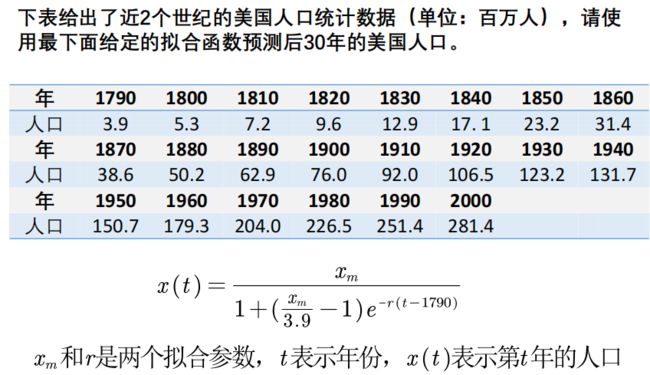
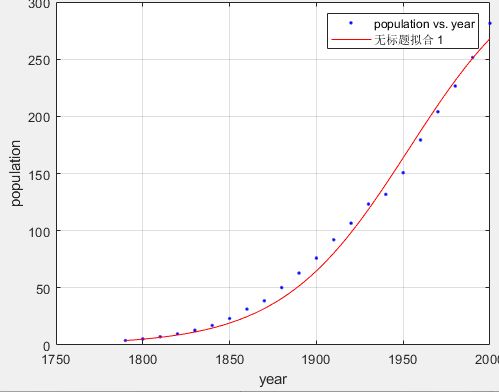
下面我们使用曲线拟合器预测美国人口

❗️ 注意：

• 该拟合函数不是线性的

参考代码：

clear;clc
year = 1790:10:2000;
population = [3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];
plot(year,population,'o')
cftool  % 拟合工具箱
% (1) X data 选择 year
% (2) Y data 选择 population
% (3) 拟合方式选择：Custom Equation (自定义方程)
% (4) 修改下方的方框为：x = f(t) = xm/(1+(xm/3.9-1)*exp(-r*(t-1790)))
% (5) 左边的result一栏最上面显示：Fit computation did not converge:即没有找到收敛解，右边的拟合图形也表明拟合结果不理想
% (6) 点击Fit Options，修改非线性最小二乘估计法拟合的初始值(StartPoint), r修改为0.02，xm修改为500 
% (7) 此时左边的result一览得到了拟合结果：r = 0.02735, xm = 342.4
% (8) 依次点击拟合工具箱的菜单栏最左边的文件—Generate Code(导出代码到时候可以放在你的论文附录)，可以得到一个未命名的脚本文件
% (9) 在这个打开的脚本中按快捷键Ctrl+S，重命名为createFit.m 将这个文件保存到当前文件夹。
% (10) 在现在这个文件中调用这个函数得到参数的拟合值和预测的效果
[fitresult, gof] = createFit(year, population)

t = 2001:2030;
xm = 342.4;   
r =  0.02735;
predictions = xm./(1+(xm./3.9-1).*exp(-r.*(t-1790)));  % 计算预测值（注意这里要写成点乘和点除,这样可以保证按照对应元素进行计算）
figure(2)
plot(year,population,'o',t,predictions,'.')  % 绘制预测结果图

预测结果图：

6 自己模拟数据演示

前置知识：

% （1）randi : 产生均匀分布的随机整数（i = int）  
%产生一个1至10之间的随机整数矩阵，大小为2x5；
s1 = randi(10,2,5)
%产生一个-5至5之间的随机整数矩阵，大小为1x10；
s2 = randi([-5,5],1,10)

%  （2） rand: 产生0至1之间均匀分布的随机数
%产生一个0至1之间的随机矩阵，大小为1x5；
s3 = rand(1,5)
%产生一个a至b之间的随机矩阵，大小为1x5；  % a + (b-a) * rand(1,5); 如：a,b = 2,5
s4= 2 + (5-2) * rand(1,5)

% （3）normrnd:产生正态分布的随机数
%产生一个均值为0，标准差（方差开根号）为2的正态分布的随机矩阵，大小为3x4；
s5 = normrnd(0,2,3,4)

% （4）roundn—任意位置四舍五入
% 0个位 1十位  2百位 -1小数点后一位  
a = 3.1415
roundn(a,-2)    % ans   =  3.1400
roundn(a,2)      % ans   =  0
a =31415
roundn(a,2)   % ans  = 31400
roundn(5.5,0)  %6
roundn(5.5,1) %10

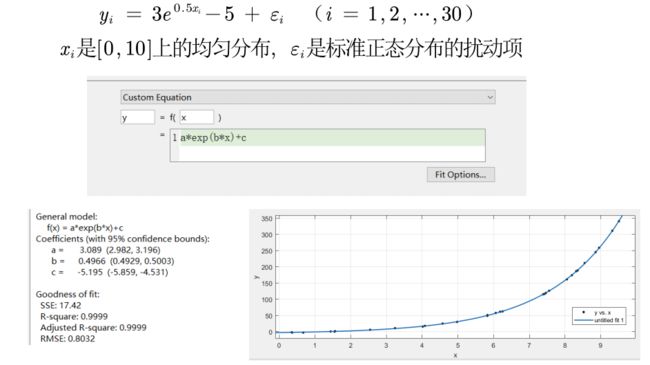
生成随机样本，使用曲线拟合器进行拟合

clear;clc 
x = rand(30,1) * 10;  % x是0-10之间均匀分布的随机向量（30个样本）
y = 3 * exp(0.5*x) -5 + normrnd(0,1,30,1);
% cftool